Fizikából kitűzött gyakorlatok és feladatok 2001. április

Beküldhető a mérési feladat és legfeljebb 5 (szabadon választható) elméleti feladat (lásd a versenykiírást).

Mérési feladat

M. 224. Csepegtetéssel vagy más módszerrel határozzuk meg, hogy a kölnivíz (illetve a húsvéti locsolásra használt bármilyen illatszer) felületi feszültsége hány százaléka a víz felületi feszültségének! (6 pont)

Közli: Radnai Gyula, Budapest

Az elméleti versenyben kitűzött gyakorlatok és feladatok

P. 3426. Két egymás melletti pályán közlekedő vonat egyike 90 km-t tesz meg óránként, a másik 10 métert másodpercenként. Az egyik vonatban ülő utas azt észleli, hogy a másik vonat 8 másodperc alatt halad el mellette. Mekkora a másik vonat hossza? (3 pont)

Jedlik Ányos verseny, Nyíregyháza

P. 3427. Egy utasszállító repülőgép a kifutópályáról 180 km/h sebességgel emelkedik fel, és egyenes vonalú pályán egyenletesen gyorsulva 40 másodperc alatt 2000 méter magasságra jut, miközben sebessége 540 km/h-ra növekszik.

a) Emelkedés közben mekkora és milyen irányú a repülőgép gyorsulása?

b) Emelkedéskor az utastér padlóján lévő börönd nem csúszik meg. Legalább mekkora a tapadási súrlódási együttható? (Tételezzük fel, hogy a padló síkja párhuzamos a sebességgel!) (4 pont)

Párkányi László verseny, Pécs

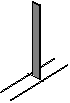
P. 3428.  Vékony, m tömegű pálca egyik végéhez merőlegesen kis tengelyt erősítettünk. A tengely az ábrán látható vízszintes sínpáron súrlódásmentesen csúszhat. Labilis egyensúlyi helyzetéből a pálca valamerre eldől.

a) Lesz-e a sínpárra ható nyonóerő valamikor nulla?

b) Elválik-e dőlés közben a pálca tengelye a síntől?

c) Mekkora a nyomóerő a 0^o-os, 90^o-os és 180^o-os elfordulás pillanatában? (5 pont)

Közli: Holics László, Budapest

P. 3429. Egy pingpongozó úgy mozgatja fel-le az ütőt, hogy a labda mindig 40 cm magasra pattan fel az ütőről. Az ütközési szám 0,5. Mekkora az ütő sebessége, amikor megüti a labdát? (A labda tömege sokkal kisebb, mint az ütőé, és a légellenállás elhanyagolható.) (4 pont)

Közli: Varga István, Békéscsaba

P. 3430. A Pireneusokban 1969 óta működtetnek egy napkohót, melyben 63 darab 30 m²-es tükör vetíti a napfényt egy kis helyre. Legalább mennyi energiát összpontosítottak a tükrök, ha 1 perc alatt 1 cm vastag, kezdetben 35 ^oC-os vaslapba 15 cm sugarú lyukat olvasztottak a napsugarak? Legalább mekkora a napkohó teljesítménye? (3 pont)

,,Keresd a megoldást!'' verseny, Szeged

P. 3431. Egy kádban T₀=80 ^oC-os víz van, a környezet T^*=20 ^oC-os. A víz hőmérséklete az idő függvényében: T(t)=T^*+(T₀-T^*)e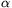^-t, ahol 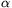a hűlésre jellemző állandó. Az első 5 percben a hőmérséklet 10 ^oC-kal csökken. Ezután mennyi idő múlva töltsünk a kádba még ugyanannyi 10 ^oC-os vizet, hogy a keverék hőmérséklete a leghamarabb érje el a 30 ^oC-ot? (5 pont)

Közli: Simon Péter, Pécs

P. 3432. Egy szabályos tetraéder csúcsaiban egyforma fémgömbök helyezkednek el. A gömbök nem érnek össze. Egyetlen (A) gömbre vitt 20 nC töltés azt ugyanakkora potenciálra tölti fel, mintha A-nak és egy másik gömbnek adnánk 15-15 nC töltést. Mekkora egyenlő töltéseket kellene adnunk A-nak és két másiknak, és mekkorát mind a négy gömbnek, hogy az A gömb potenciálja mindig ugyanakkora legyen? (6 pont)

Közli: Bihary Zsolt, Irvine, California

P. 3433. Egy régi voltmérő az 1 V-os méréshatáron 0,7 V-nak, a 10 V-os méréshatáron 2,6 V-nak méri ugyanannak a telepnek a feszültségét. Mit mutat a voltmérő 100 V-os méréshatáron? (4 pont)

Romániai feladat nyomán

P. 3434. Határozzuk meg az ábrán látható, csupa 1 k\(\displaystyle Omega\)-os ellenállásból álló végtelen hálózat eredő ellenállását az A és C, illetve az A és B pontok között! (6 pont)

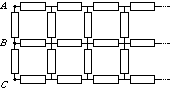
Közli: Gnädig Péter, Budapest

P. 3435. A hálózati váltófeszültségre egy 0,2 H induktivitású és 62,8 \(\displaystyle Omega\) ohmos ellenállású tekercset kapcsoltunk.

a) Mekkora kapacitású kondenzátor kapcsolható sorba a tekerccsel anélkül, hogy a hasznos teljesítmény megváltozna? Változik-e a teljesítménytényező értéke?

b) Javítható-e a teljesítménytényező azáltal, hogy a tekerccsel párhuzamosan egy kondenzátort kapcsolunk? Növelhető-e 1-re a teljesítménytényező? (4 pont)

Vermes Miklós verseny, Sopron

P. 3436. Nevenincs csillag egyik bolygója hosszú, henger alakú. A bolygó átlagsűrűsége ugyanakkora, mint a Földé, sugara is megegyezik a Föld sugarával, tengelyforgási ideje pedig éppen 1 nap.

a) Mekkora az első kozmikus sebesség ennél a bolygónál?

b) A bolygó felszíne felett milyen magasan keringenek az ottani távközlési szinkron-műholdak?

c) Mekkora a második kozmikus sebesség ennél a bolygónál? (5 pont)

Közli: Horányi Gábor, Budapest

A fizika feladatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 2001. május 11.