Fizikából kitűzött gyakorlatok és feladatok 2001. május

Beküldhető a mérési feladat és legfeljebb 5 (szabadon választható) elméleti feladat (lásd a versenykiírást).

Mérési feladat

M. 225. Ejtsünk tiszta vízbe egy csepp olajat! Mérjük meg, hogyan függ a ,,behatolási mélység'' az ejtés magasságától és a csepp méretétől! (6 pont)

Közli: Bodrogi Péter, Budapest

Az elméleti versenyben kitűzött gyakorlatok és feladatok

P. 3437. 2 cm vastag, 0,5 kg/dm³ sűrűségű fakorong úszik a vizen.

a) Milyen vastag, ugyanolyan alapterületű alumíniumkorongot tehetünk a tetejére, hogy a fa ne legyen teljesen a víz alatt?

b) Mi a válasz akkor, ha alulra erősítjük fel az alumíniumkorongot? (3 pont)

Közli: Holics László, Budapest

P. 3438. Rézből és nikkelből 1:1 arányú ötvözetet készítünk. Mekkora lesz az így keletkező ötvözet sűrűsége, ha a két fém térfogatváltozás nélkül elegyedik? (4 pont)

Közli: Tasnádi Péter, Budapest

P. 3439. Egy 200 N/m rugóállandójú rugón két 1 kg-os test függ egy 10 cm hosszú fonállal összekötve, az ábrán látható módon. A fonalat elégetjük. Mekkora lesz a távolság a két test között, amikor a felső test először kerül legmagasabb helyzetébe?

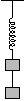
(4 pont)

Közli: Szabó Zoltán, Budapest

P. 3440. Légpárnás asztalon a kezdetben nyújtatlan, l₀ hosszúságú húzó-nyomó rugó egyik vége rögzített, a másik végéhez egy m tömegű kis korongot erősítünk. Meglökjük a korongot a rugó hosszára merőlegesen, v₀ kezdősebességgel. A kialakuló mozgás során a rugó legnagyobb megnyúlása \(\displaystyle Delta\)l=l₀/10. Mekkora a rugóállandó? Vázoljuk fel a korong középpontjának pályagörbéjét!

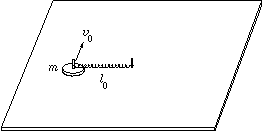
(5 pont)

Közli: Simon Péter, Pécs

P. 3441. Bizonyos mennyiségű egyatomos ideális gáz kétféleképpen jut el az ábrán látható A állapotból a B állapotba: vagy az AB, vagy az ACB úton. Az ACB úton a gáz által felvett hő csak 90 %-a az AB úton felvett hőnek. Kezdetben (az A állapotban) a gáz hőmérséklete 150 K. Mekkora a gáz hőmérséklete a C állapotban, és mekkora a B állapotban?

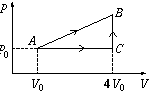
(5 pont)

Közli: Kotek László, Pécs

P. 3442. A \(\displaystyle 2\,\ell\) hosszúságú tükör percenként 10-et fordul a tükör O felezőpontján átmenő, az ábra síkjára merőleges tengely körül. Az O középpontú, R sugarú kör A pontjában egy fényforrás, a B pontjában egy megfigyelő van (AOB\(\displaystyle szog\)=90^o).

a) Milyen görbén mozog az A pontszerű fényforrás tükörbeli látszólagos képe?

b) Milyen sebességgel mozog A látszólagos képe?

c) Mekkora az \(\displaystyle R/\ell\) arány, ha a B megfigyelő a tükör \(\displaystyle phi\)=15^o-os állásánál pillantja meg először a fényforrást?

d) Egyfolytában mennyi ideig láthatja a megfigyelő a tükörben a fényforrást ilyen \(\displaystyle R/\ell\) arány mellett?

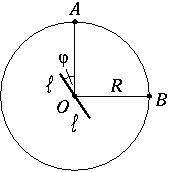
(5 pont)

Közli: Gálfi László, Budapest

P. 3443. Egy 100 eV mozgási energiájú elektron a lemezekkel 30^o-os szöget bezáró sebességgel lép be két sűrű fémrácsból kialakított síkkondenzátor lemezei közé, és 45^o-os szögben lép ki a lemezek közül.

Mekkora a kondenzátor feszültsége, és mekkora mozgási energiával hagyja el az elektron a kondenzátort?

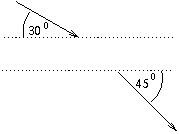
(4 pont)

Közli: Varga István, Békéscsaba

P. 3444. Egy ,,szuperellipszis'' egyenlete: (x/a)⁴+(y/b)⁴=1, ahol a és b a féltengelyek hossza.

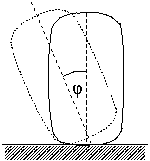
Egy szuperellipszis keresztmetszetű homogén hengert nagyobb féltengelyével függőleges helyzetben vízszintes asztallapra állítunk. Határozzuk meg (numerikus, geometriai vagy analitikus módszerekkel), hogy mekkora 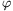szögű kibillentésig stabil az ábrán látható helyzet! Ábrázoljuk \(\displaystyle phi\)-t a b/a ,,lapultsági arány'' függvényében!

(6 pont)

Közli: Gnädig Péter, Budapest

A fizika feladatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 2001. június 11.