Solutions for exercises "C" in September, 2001

In this page only the sketch of the solutions are published; in some cases only the final results. To achieve the maximum score in the competition more detailed solutions needed.

C. 635. In an arithmetic class, pupils are asked how many legs a hen, six dogs and seven palpigradis have in total. (``Palpigradi'' is the Latin name of a certain animal). Alex says 46, Ben says 52, Cecilia says 66, Dora says 78, and Edith says 82. Who is right?

Based on a problem of a Zrínyi Competition

Solution. If the number of legs of a palpigradi is x, then the total number of legs is 2+6^.4+7^.x=7(x+3)+5. Thus the remainder of the number of legs divided by 7 is 5. 82 is the only number out of 46, 52, 66, 78 and 82 that leaves a remainder of 5 when divided by 7, therefore only Edith can be right.

By solving the equation 2+6^.4+7^.x=82, we also learn that a palpigradi has 8 legs.

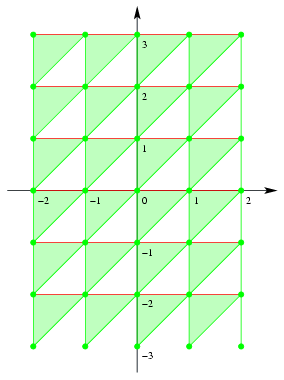
C. 636. In the Cartesian coordinate system, represent the set of points whose coordinates x and y satisfy -2\(\displaystyle le\)x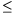2, -3\(\displaystyle le\)y\(\displaystyle le\)3, {x}\(\displaystyle le\){y} ({z} denotes the difference between the number z and the greatest integer less than or equal to z.)

Solution. For points in the interior of the unit square, the braces denoting fractional part can be omitted from the third inequality, as the coordinates of the points are equal to their fractional parts. Thus it is enough to find out which points have coordinates that satisfy x\(\displaystyle le\)y. Such points lie on and above the line of equation y=x. The set contains the vertical sides and the vertices of the unit square, where {x}=0; whereas the interior points of the horizontal sides, where {y}=0, do not belong to the set.

By also considering the first and second inequalities, the following set is obtained. (The set consists of the green triangles, segments and points, the red segments do not belong to the set.)

C. 637. Find the positive integer that has two digits both in base 10 and in base 8, and for which the sum of the digits is fourteen in both number systems.

Solution. Write down both forms of the number:

a^.10²+b^.10+c=x^.8²+y^.8+z.

From both sides, subtract the sum of the digits i.e. 14:

99a+9b=63x+7y.

Subtracting 63x,

99a+9b-63x=7y.

The left-hand side is now divisible by 9, therefore so is the right- hand side. Hence the value of y is 9 or 0. But base-eight notation has no figure of 9, thus the value of y is 0.

The condition x+y+z=14 now implies x+z=14. As x and z are at most 7 and their sum is 14, x and z are both equal to 7. Hence the number in question is 707 in base-eight notation, which means 455 in decimal notation.

C. 638. How many different square prisms are possible in which the lengths of the edges in cm are integers and the measure of the surface area in cm² equals the measure of the volume in cm³?

Solution. Let n denote the base edge of the square-based prism, and let k denote its height. From the equality of volume and surface area,

n²k=2n²+4nk.

Dividing by n, and rearranging:

nk-2n-4k=0.

With 8 added to both sides, the left-hand side can be factored:

(n-4)(k-2)=8.

The possible factorisations of 8 are 8^.1, 4^.2, 2^.4, 1^.8. Negative factors are not allowed, as n-4>-4 and k-2>-2. This means four solutions for (n,k): (12,3); (8,4); (6,6) és (5,10). Therefore, the conditions are satisfied by four different prisms.

C. 639. How many pairs (a;b) of positive integers are there with 1\(\displaystyle le\)a\(\displaystyle le\)2001, 1\(\displaystyle le\)b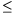2001, where the lowest common multiple of a and b is 2001?

Solution. The resolution of 2001 into prime factors is 3^.23^.29. Thus the prime factor resolutions of the two numbers are a=3^k.23^m.29ⁿ, and b=3^p.23^q.29^r, where all exponents can be 0 or 1.

The pairs (k,p), (m,q) and (n,r) can be of three kinds: (0,1), (1,0) and (1,1). (0,0) is not possible. The three pairs of exponents can be selected independently of each other. For example, if the three pairs of exponents are (0,1), (1,1) and (0,1), then the number pair a=3^0.23^1.29⁰, b=3^1.23^1.29¹ is obtained.

Thus the number of possible number pairs (a,b) is 3³=27.