 |
Solutions for theoretical problems in PhysicsSeptember, 2001 |
In this page only the sketch of the solutions are published; in some cases only the final results. To achieve the maximum score in the competition more detailed solutions needed.
P. 3445. Julie and Steve live in the same street, Julie in a 300 m and Steve in a 800 m distance from the school. In the morning they leave for school at the same time. Steve goes by bike at a speed of 10 m/s and Julie goes on foot at a speed of 2 m/s. When they meet, Steve gets off his bike and they walk on together talking to each other at a speed of 1 m/s. Will they reach the school before the school bell rings if they started from home 3 minutes before the ring? (3 points)
Solution. Julie and Steve will late roughly one minute if they live in the same direction, or late about half a minute (28 s), if they live in the opposite sides of the school.
P. 3446. There is a force of 800 N exerted on a man standing in a lift due to gravitation. The force exerted on the lift by the man (his weight) is 820 N. At what rate does the lift accelerate and in which direction? What can we say of the velocity of the lift? (3 points)
Solution. Let a be the upwards acceleration (or the downwards deceleration) of the lift, then
\(\displaystyle mg=800~{\rm N},\quad m(g+a)=820~{\rm N}\quad\longrightarrow\quad a=0.025~g\approx0.25~{\rm m/s}^2.\)
We can not say anything of the velocity.
P. 3447. Let's fill an air-balloon to the same volume once with hydrogen and once with helium. In which case is the lifting capacity greater and by what percentage? (In the given conditions the gas densities in kg/m3 units are: hydrogen -- 0.08, helium -- 0.16, air -- 1.162). The mass of the balloon's material is negligible compared to the mass of the burden and the volume of the burden is negligible compared to the volume of the balloon. (3 points)
Solution. The ratio of the lifting forces is
\(\displaystyle {\rho_{\rm air}-\rho_{\rm H}\over\rho_{\rm air}-\rho_{\rm He}}=1.08.\)
P. 3448. Let's push up a crate of a mass of 10 kg slowly on a slope. The work needed to achieve this is 400 J. By pulling the same crate down the slope we use work of 250 J. (The force of both pushing and pulling is parallel to the direction of the slope.) What is the height of the slope? (4 points)
Solution.
L1=mg(sin\(\displaystyle alpha\)+\(\displaystyle mu\)cos\(\displaystyle alpha\))\(\displaystyle ell\)=400 J, L2=mg(\(\displaystyle mu\)cos\(\displaystyle alpha\)-sin\(\displaystyle alpha\))\(\displaystyle ell\)=250 J,
so the height of the slope is
\(\displaystyle h=\ell\cdot\sin\alpha={L_1-L_2\over2mg}\approx76~{\rm cm}.\)
P. 3449. There are three elastic disks with masses m1=m3=0.15 kg, m2=0.2 kg connected with two equal length strings of negligible mass, on a horizontal air-cushioned table. At the beginning the three disks are in rest and reside in one line (according to the figure). Then we make the middle disk move horizontally and perpendicular to the strings with a velocity of v0=6 m/s.
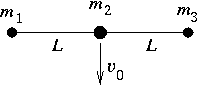
a) What is the velocity of the side disks right at the moment when the disk of mass m2 stops after the elastic collision of the two disks in question? What is the angle formed by the two strings in this position?
b) What is the angle formed by the two strings in this position? (6 points)
Solution. Using the conservation laws of energy and momentum
\(\displaystyle {1\over2}m_2v_0^2=m_1v^2,\quad m_2v_0=2m_1v\sin\alpha,\)
where 2\(\displaystyle alpha\) is the angle of the two strings. From these equations follow v=4.9 m/s and 2\(\displaystyle alpha\)=110o.
P. 3450. There is a ship sailing east along the Equator with a speed of 45 km/h. How much time does a pendulum-clock on board lose in 3 hours if it keeps good time when the ship rests relative to the Earth. (5 points)
Solution. If the gravitation force acting on a body of mass m at the Equator is mg0, then the measurable gravitational acceleration on the board of a ship (motionless relative to the Earth) g=g0-vE2/R, where vE is the speed of the points of the Equator due to the rotation of the Earth.
If the ship is moving (relative to the Earth) with a speed v, the `effective' gravitational acceleration on the board is
\(\displaystyle g^{\prime}=g_0-{(v_{\rm E}+v)^2\over R}\approx g-2{vv_{\rm E}\over R}.\)
(We have neglected the smallest term proportional to v2/R, because v\(\displaystyle ll\)vE.) The period of the pendulum-clock (\(\displaystyle T^{\prime}\)) on a moving ship is larger, then the period (T) on a motionless ship. The ratio of the periods is
\(\displaystyle {T^{\prime}\over T}=\sqrt{{g\over g^{\prime}}}=\sqrt{{g\over g-2vv_{\rm E}/R}}\approx\left(1-{vv_{\rm E}\over gR}\right)^{-1}.\)
The moving pendulum-clock will lose in t=3 hours
\(\displaystyle \Delta t=\left(1-{T\over T'}\right)t\approx{vv_{\rm E}\over gR}t.\)
Using the data (vE=463 m/s, v=12.5 m/s, R=6.37.106 m and g\(\displaystyle approx\)10 m/s2) \(\displaystyle Delta\)t\(\displaystyle approx\)1.0 s.
P. 3451. A solid piece of metal with a volume of 50 cm3 and a temperature of 20 oC can be lifted to a height of 100 m by using 135 J of work. What would be the temperature of the same object if we transmitted to it an amount of heat equivalent to the work used in lifting. (4 points)
Solution. Using the given value of the lifting work E=mgh=135 J (g\(\displaystyle approx\)10 m/s2, h=100 m) one can calculate the mass and the density of the metal: m=0.135 kg, \(\displaystyle rho\)=2.7g/cm3. Presumably the metal is aluminium, its specific heat is c=900 J/kgoC, therefore the change of its temperature would be \(\displaystyle Delta\)T=E/(\(\displaystyle rho\)Vc)=1.1oC.
P. 3452. The measuring limit of a standard
voltage meter with the resistance of R=1 k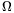 can be extended to
60 V, 150 V and 300 V as can be seen in the
figure. The sum of the three additional resistances is
9 k\(\displaystyle Omega\). What are
the separate resistance values, and how much is the measuring limit of
the basic instrument U0? (4 points)
can be extended to
60 V, 150 V and 300 V as can be seen in the
figure. The sum of the three additional resistances is
9 k\(\displaystyle Omega\). What are
the separate resistance values, and how much is the measuring limit of
the basic instrument U0? (4 points)
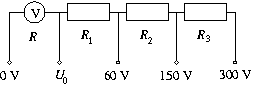
Solution. The intensity of currents of the voltage meter at the measuring limit should be the same:
\(\displaystyle {R+R_1\over60}={R+R_1+R_2\over150}={R+R_1+R_2+R_3\over300}.\)
From the known data (R=1 k\(\displaystyle Omega\) and R1+R2+R3=9 k\(\displaystyle Omega\)) one can calculate the resistance values: R1=1 k\(\displaystyle Omega\), R2=3 k\(\displaystyle Omega\) and R3=5 k\(\displaystyle Omega\).
Since R1=R, the measuring limit of the basic instrument is U0=30 V.
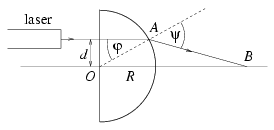
P. 3453. A semicylinder made of a transparent plastic has a refraction index of n=1.41 and a radius of R=5 cm. There is a narrow incident laser beam perpendicular to the flat side of the semicylinder at d distance from the axis of symmetry.
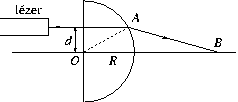
a) What can the maximum value of d be so that the laser beam can still leave the other side of the semicylinder?
b) How can the refraction index be determined if we know dmax and R?
c) By varying distance d, in which interval will distance OB shown in the figure vary? (4 points)
Solution. Using the notations of the figure and Snell's law:
\(\displaystyle {\sin\psi\over\sin\phi}=n.\)
a) At d=dmax \(\displaystyle psi\)=90o, so sin\(\displaystyle phi\)=1/n.
b) sin\(\displaystyle phi\)=dmax/R, therefore n=R/dmax. With the given value of n dmax=3.55 cm.
c) In general case \(\displaystyle \overline{OB}\)
\(\displaystyle f=\overline{OB}=R\left(\cos\phi+{\sin\phi\over{\rm tg}(\psi-\phi)}\right)\)
In the limiting case \(\displaystyle psi\)=90o, so
\(\displaystyle f_1={R\over\cos\phi}=R{n\over\sqrt{n^2-1}}=7.1~{\rm cm}.\)
If d goes to zero, all of the angles will be small, therefore sin\(\displaystyle psi\)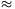
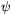 , cos
, cos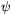
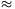 1, tg(
1, tg(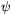 -
-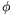 )
)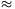 (
(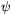 -
-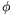 ), and
), and 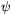 /
/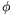
 n, thereupon
n, thereupon
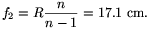
Varying d the distance 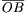 will vary between f1 and f1.
will vary between f1 and f1.
P. 3454. In 1923 George Hevesy determined the age of a rock sample with some uranium content based on the finding that the ratio of the number of 238U atoms to the number of 206Pb atoms present in the sample was 3:2. What was the age he determined? (4 points)
Solution.
The number of 238U atoms at time t is
N(0)(1-e-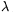 t),
t),
and the number of 206Pb atoms should be
N(0)(1-e-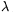 t),
t),
where N(0) is the number of 238U atoms at the formations of the rock. The ratio of U and Pb atoms is
N(0)e-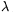 t:N(0)(1-e-
t:N(0)(1-e-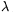 t)=3:2,
t)=3:2,
that is e-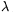 t=3/5, so
t=3/5, so
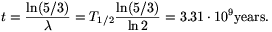
P. 3455. The Sun emits electromagnetic radiation with the power of 3.86x1026 W.
a) How much energy arrives per second at the top of the Earth's atmosphere on a 1 m2 surface perpendicular to the radiation coming from the Sun?
b) How much is the impulse of the light incident on a surface of 1 m2 in one second?
c) What is the pressure exerted by the incoming light on a surface that is perpendicular to the radiation and absorbs every kind of light? (4 points)
Solution. a) The energy current density of the Sun is J=LSun/(4R2 )=1.36 kW/m2, where R is the distance of the Sun and the Earth.
)=1.36 kW/m2, where R is the distance of the Sun and the Earth.
b) The energy of the light is proportional to its momentum (the constant of proportionality is the speed of the light). So the momentum of the light per second and unit surface is 4.6.10-6 kg m/s.
c) The pressure of the absorbed light is equal to the momentum change per second: p=4.6.10-6 N/m2.
