Matematikából kitűzött gyakorlatok és feladatok
2001. szeptember

Kérjük, olvassa el a versenykiírást.

A C pontversenyben kitűzött gyakorlatok

Minden C-jelű feladat helyes megoldásáért 5 pont jár.

C. 635. Számtanórán megkérdezték a gyerekeket, hogy hány lába van összesen egy tyúknak, hat kutyának és hét palpigradinak (a palpigradi egy állat latin neve). Aladár szerint 46, Benő szerint 52, Cecília szerint 66, Dóra szerint 78, Eufrozina szerint pedig 82. Melyiküknek van igaza?

Zrínyi verseny feladata alapján

C. 636. Ábrázoljuk a derékszögű koordinátarendszerben azokat a pontokat, amelyek koordinátáira

-2$\displaystyle le$x$\displaystyle le$2, -3$\displaystyle le$y$\displaystyle le$3, {x}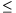{y}.

(A {z} a z szám törtrészét jelöli.)

C. 637. Melyik az a pozitív egész szám, amely a tízes és a nyolcas számrendszerben is háromjegyű, továbbá számjegyeinek összege mindkét esetben tizennégy?

C. 638. Hány olyan négyzetes oszlop van, amelyben az élek cm-ben mért mérőszáma egész szám, és a felszín mérőszáma cm²-ben megadva annyi, mint a térfogat mérőszáma cm³-ben megadva?

C. 639. Hány olyan pozitív egész számokból álló (a;b) számpár van, amelyre

1$\displaystyle le$a$\displaystyle le$2001, 1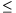b$\displaystyle le$2001,

és az a és b számok legkisebb közös többszöröse 2001?

A B pontversenyben kitűzött feladatok

A B-jelű feladatokra kapható pontszám a feladatok nehézségétől függ. Minden hónapban a 6 legnagyobb pontszám számít be a pontversenybe.

B. 3472. Hány olyan időpont van reggel 6 és este 6 óra között, amikor nem tudjuk kitalálni az óráról a pontos időt, ha nem tudjuk megkülönböztetni a nagy- és a kismutatót? (3 pont)

Kvant

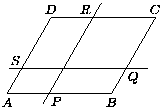
B. 3473. A 2 egységnyi területű ABCD paralelogrammában az AD-vel párhuzamos egyenes a P és az R, az AB-vel párhuzamos egyenes pedig az S és a Q pontokban metszi a paralelogramma kerületét az ábra szerint. Mekkora az AQR, BRS, DPQ és CSP háromszögek területének összege? (3 pont)

B. 3474. Határozzuk meg az 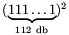$({\underbrace{111\dots1}_{112~{\rm db}}})^2$ hátulról számított hetvenharmadik számjegyét. (4 pont)

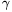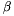B. 3475. Az a, b, c oldalú háromszög szögei $\displaystyle alpha$, $\displaystyle beta$, gamma . Igazoljuk, hogy ha 3$\displaystyle alpha$+2 beta =180^o, akkor a²+bc-c²=0. (4 pont)

Nemzetközi Magyar Matematika Verseny, 2001

B. 3476. Egy szabályos 10 oldalú sokszög egy tetszőleges belső pontját a sokszög csúcsaival összekötve 10 darab háromszöget kapunk. A háromszögeket adott körüljárás szerint felváltva pirosra, illetve kékre festjük. Bizonyítsuk be, hogy a kék területek összege egyenlő a piros területek összegével. (4 pont)

B. 3477. Legfeljebb mekkora lehet a 2ⁿ fokos szög szinusza, ha n pozitív egész? (4 pont)

B. 3478. Az ABC háromszög hozzáírt köreinek középpontjai O₁, O₂, O₃. Bizonyítsuk be, hogy O₁O₂O₃ háromszög területe legalább négyszerese ABC háromszög területének. (4 pont)

Javasolta: Besenyei Ádám, Budapest

B. 3479. Keressük meg a 6t²+3s²-4st-8t+6s+5 kifejezés minimumát. (4 pont)

B. 3480. Adottak az e egyenesen az A, B, C és D pontok ebben a sorrendben. Mi azon P pontok mértani helye a síkban, amelyekre az APB és a CPD szögek egyenlők? (5 pont)

Gillis--Turán matematikaverseny, 2001.

B. 3481. Legyen $\displaystyle f_1(x)=-{{2x+7}\over{x+3}}$, f_n+1(x)=f₁(f_n(x)). Határozzuk meg f₂₀₀₁(2002) értékét. (4 pont)

Az A pontversenyben kitűzött nehezebb feladatok

Minden A-jelű feladat helyes megoldásáért 5 pont jár.

A. 269. Egy kör keresztmetszetű lyukat két 1 méter oldalú négyzetlappal szeretnénk hézagmentesen lefedni. Milyen határok között mozoghat a lyuk átmérője?

A. 270. Igazoljuk, hogy tetszőleges a, b, c, d pozitív számokra

$\displaystyle \root3\of{abc+abd+acd+bcd\over4}\leq\sqrt{{{ab+ac+ad+bc+bd+cd}\over6}}.$

A. 271. Bizonyítsuk be, hogy tetszőleges p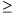5 prímszámra

\(\displaystyle \sum_{0 osztható p²-tel.

Vojtech Jarnik matematikaverseny, Ostrava, 2001

A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:

KöMaL Szerkesztőség

Budapest 112, Pf. 32. 1518

illetve

megoldas@komal.elte.hu

tájékoztatónkat

Már regisztráltál?
Új vendég vagy?