 |
Exercises and problems in Informatics |
Please read The Conditions of the Problem Solving Competition.
I. 4. A prime number is called very prime, if all of its initial slices are also prime numbers. 239 for example, is a very prime number, because 2, 23 and 239 are all primes. The prime number 241 on the other hand, is not a very prime number, because--although 2 is prime--24 is not. Write a program that displays all very prime numbers having N digits (1\(\displaystyle le\)N\(\displaystyle le\)8) and all of their initial slices. Correct solutions are ranked according to their speed. (10 points) Example (N=3): 2, 23, 233 2, 23, 239 2, 29, 293 3, 31, 311...
I. 5. Write a program which displays a unit cube, firstly as a wire frame object and secondly with invisible hidden parts. The centre of the cube should be the origin and it is to be viewed from the direction of the z-axis from a given distance. The program should be able to rotate the cube around an arbitrary co-ordinate axis. (10 points)
I. 6. We want to simulate the oscillations of a spring using
the following model. By carefully hanging a body with mass M on
the ``ideal'' spring (i.e. its mass is neglected), the spring expands
until it keeps its balance. Now we stretch the spring with the body to
have length L, and let it oscillate. This motion is to be
simulated by choosing an appropriately short time interval (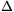
t) and
computing the instant elongation, the resulting force (which comes
from the weight of the body with mass M and the elongation of
the spring), the acceleration and the velocity. Write an Excel
spreadsheet (RUGO.XLS) to simulate this phenomenon.
a) Give the quantities F (resulting force), a (acceleration), v (velocity) and l (elongation) in the first 200 timesteps.
b) Plot the change of the elongation.
c) The parameters of the model (the spring constant
D, the constant of friction KE, the initial elongation
L, the mass M of the body and the time interval 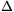t)
should be indicated in the upper left corner of your sheet (and they
are possibly modifiable).
d) How does the simulation change if friction is also taken into account? (10 points)