A 2001. novemberi A-jelű matematika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

A. 275. Egy nxn-es táblázatba beírjuk sorban az 1², 2², 3², ..., (n²)² számokat:

1²	2²	...	n²
(n+1)²	(n+2)²	...	(2n)²
...	...		...
(n²-n+1)²	(n²-n+2)²	...	(n²)²

Minden sorból kiválasztunk egy-egy számot úgy, hogy semelyik kettő ne legyen ugyanabban az oszlopban.

Mik a kiválasztott számok összegének lehetséges értékei?

Terpai Tamás ötletéből

Megoldás. Tegyük fel, hogy az i-edik sorból rendre az a_i-edik elemet választottuk ki. (i=1,2,...,n.) Az a₁,...,a_n számok az 1,2,...,n egy permutációja, a kiválasztott számok összege pedig

$\displaystyle \sum_{i=1}^n\big((i-1)n+a_i\big)^2=n^2\sum_{i=1}^n(i-1)^2+\sum_{i=1}^na_i^2+2n\sum_{i=1}^n(i-1)a_i.$

Az első két összeg értéke nem függ az a_i-k kiválasztásától:

$\displaystyle n^2\sum_{i=1}^n(i-1)^2=n^2\cdot{(n-1)n(2n-1)\over6}={n^3(n-1)(2n-1)\over6},$

$\displaystyle \sum_{i=1}^na_i^2=\sum_{i=1}^ni^2={n(n+1)(2n+1)\over6}.$

A harmadik összeg a rendezési tétel szerint akkor a legkisebb, illetve legnagyobb, amikor az a_i számok csökkenő, illetve növekvő sorozatot alkotnak. Ezért a legkisebb és legnagyobb érték

$\displaystyle 2n\sum_{i=1}^n(i-1)(n-i+1)=2n\cdot{(n-1)n(n+1)\over6},$

illetve

$\displaystyle 2n\sum_{i=1}^n(i-1)i=2n\cdot{(n-1)n(n+1)\over3}.$

Egy kis számolással ellenőrizhető, hogy n kis értékeire 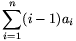$\sum_{i=1}^n(i-1)a_i$ lehetséges értékei a következők:

n	$\sum_{i=1}^n(i-1)a_i$ lehetséges értékei
1	0
2	1, 2
3	4, 5, 7, 8
4	10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20

Indukcióval bizonyítjuk, hogy n$\displaystyle ge$5 esetén 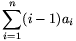$\sum_{i=1}^n(i-1)a_i$ minden egész értéket felvesz 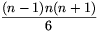${(n-1)n(n+1)\over6}$ és $\displaystyle {(n-1)n(n+1)\over3}$ között. Mint láttuk, n=4 esetén ez igaz.

Ha az állításunk igaz valamely n=m-re, akkor n=m+1 esetén vizsgáljuk meg azokat az a₁,...,a_m+1 sorozatokat, amikor a_m+1=m+1 illetve a₁=m+1.

Abban az esetben, amikor a_m+1=m+1,

$\displaystyle \sum{i=1}^n(i-1)a_i=\sum_{i=1}^ma_i+(m-1)m,$

és ugyanazokat az összegeket kapjuk, mint az n=m esetben, csak m(m+1)-gyel megnövelve. Az ilyen összegek tehát az $\displaystyle A={(m-1)m(m+1)\over6}+m(m+1)$ és 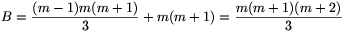$B={(m-1)m(m+1)\over3}+m(m+1)={m(m+1)(m+2)\over3}$ közötti egészek.

Ha a₁=m+1, akkor

$\displaystyle \sum_{i=1}^n(i-1)a_i=\sum_{i=2}^{m+1}(i-1)a_i=\sum_{i=1}^mia_{i+1}=$

$\displaystyle =\sum_{i=1}^m(i-1)a_{i+1}+\sum_{i=1}^na_{i+1}=\sum_{i=1}^m(i-1)a_{i+1}+{m(m+1)\over2},$

ezért ebben az esetben is ugyanazokat az összegeket kapjuk, de ezúttal $\displaystyle {m(m+1)\over2}$-vel növelve. A kapott összegek tehát a 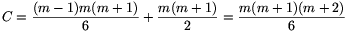$C={(m-1)m(m+1)\over6}+{m(m+1)\over2}={m(m+1)(m+2)\over6}$ és $\displaystyle D={(m-1)m(m+1)\over3}+{m(m+1)\over2}$ közötti egészek.

Könnyen ellenőrizhető, hogy m$\displaystyle ge$4 esetén C<A $le$ D<B, ezért az összes C és B közötti egész előáll. Ezzel állításunkat igazoltuk.

A végeredmény: a táblázatból kiválasztott elemek összegének lehetséges értékei n$\displaystyle ne$3 esetén egy számtani sorozatot alkotnak, amelynek legkisebb eleme

$\displaystyle {n^3(n-1)(2n-1)\over6}+{n(n+1)(2n+1)\over6}+2n\cdot{(n-1)n(n+1)\over6}={n(2n^4-n^3+3n^2+n+1)\over6},$

legnagyobb eleme

$\displaystyle {n^3(n-1)(2n-1)\over6}+{n(n+1)(2n+1)\over6}+2n\cdot{(n-1)n(n+1)\over3}={n(2n^4+n^3+3n^2-n+1)\over6},$

differenciája pedig 2n.

Az n=3 esetben az eredmény hasonló, de a sorozat középső eleme, a 95 nem áll elő; a lehetséges értékek 83, 89, 101 és 107.

A. 276. Az x₁, ..., x_n pozitív számok szorzata 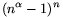$(n^\alpha-1)^n$ , ahol $alpha$ $ge$ 1 valós szám. Bizonyítsuk be, hogy

$\displaystyle \sum_{i=1}^n{1\over(x_i+1)^{1/\alpha}}\ge1.$

Megoldás. Legyen $\displaystyle f(t)={1\over(t+1)^{1/\alpha}}$. Be fogjuk bizonyítani a következő két lemmát:

1. lemma. Ha a$\displaystyle le$b$\displaystyle le$c$\displaystyle le$d pozitív számok és ad=bc, akkor

$\displaystyle f(a)+f(d)\ge\min\big(f(b)+f(c),1\big).$

2. lemma. Ha az x₁,x₂,...,x_n számok mértani közepe m, akkor

$\displaystyle f(x_1)+f(x_2)+\dots+f(x_n)\ge\min\big(n\cdot f(m),1\big).$

A feladat állítása a 2. lemma speciális esete, ugyanis ha az x₁,...,x_n pozitív számok szorzata (n^{$\displaystyle alpha$}-1)ⁿ, azaz a mértani közepük m=n^{$\displaystyle alpha$}-1, akkor n^.f(m)=1.

Az 1. lemma bizonyítása. Legyen 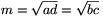$m=\sqrt{ad}=\sqrt{bc}$ , tetszőleges pozitív t esetén

$\displaystyle g(t)=f(mt)+f(m/t)=\bigg(mt+1\bigg)^{-{1\over\alpha}}+\bigg({m\over t}+1\bigg)^{-{1\over\alpha}},$

továbbá t₁=c/m és t₂=d/m. Ekkor 1 $le$ t₁$\displaystyle le$t₂, és a bizonyítandó állítás az, hogy

$\displaystyle g(t_2)\ge\min\big(g(t_1),1\big).$

A definícióból látható, hogy $\displaystyle \lim\limits_\infty g=1.$

Vizsgáljuk meg a g függvényt az [1, $infty$ ) intervallumon monotonitás szempontjából. A g függvény deriváltja

$\displaystyle g'(t)={m\over\alpha}\left(-\bigg(mt+1\bigg)^{-{\alpha+1\over\alpha}}+{1\over t^2}\bigg({m\over t}+1\bigg)^{-{\alpha+1\over\alpha}}\right).$

ami akkor és csak akkor pozitív, ha

$\displaystyle \bigg(mt+1\bigg)^{\alpha+1\over\alpha$t^2\bigg({m\over t}+1\bigg)^{\alpha+1\over\alpha}.">

$\displaystyle {\alpha\over\alpha+1}$-edik hatványra emelve és rendezve:

$\displaystyle t^{2\alpha\over\alpha+1}-mt+mt^{\alpha-1\over\alpha+1}-1<0.$

Jelöljük a baloldalt h(t)-vel. A további diszkusszióhoz szükségünk lesz a h függvény első két deriváltjára, valamint a h(1) és h'(1) értékére. Tehát,

$\displaystyle h(t)=t^{2\alpha\over\alpha+1}-mt+mt^{\alpha-1\over\alpha+1}-1,\qquad h(1)=0;$

$\displaystyle h'(t)={2\alpha\over\alpha+1}t^{\alpha-1\over\alpha+1}-m+{\alpha-1\over\alpha+1}mt^{-{2\over\alpha+1}},\qquad h'(1)={2\over\alpha+1}(\alpha-m);$

$\displaystyle h''(t)={2\alpha(\alpha-1)\over(\alpha+1)^2}t^{-{\alpha+3\over\alpha+1}}\bigg(t-{m\over\alpha}\bigg).$

Ezután több esetet fogunk vizsgálni aszerint, hogy m és $alpha$ mekkora.

1. eset: $\displaystyle alpha$=1 és m$\displaystyle le$1.

2. eset: $\displaystyle alpha$=1 és m>1.

3. eset: $\displaystyle alpha$>1 és m$\displaystyle le$ $alpha$ .

4. eset: $alpha$ >1 és m> $alpha$ .

Az 1. esetben tetszőleges t>1-re h(t)=(1-m)(t-1) $ge$ 0, tehát a (1,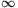 $infty$ ) intervallumban h $ge$ 0.

A 2. esetben tetszőleges t>1-re h(t)=(1-m)(t-1)<0, tehát az (1,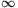 $infty$ ) intervallumban h<0.

A 3. esetben h'(1) $ge$ 0 és t>1 esetén h''>0, tehát a teljes (1,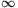 $infty$ ) intervallumban h'>0. Mivel h(1)=0, ebből következik, hogy az (1,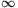 $infty$ ) intervallumban h>0.

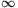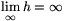A 4. esetben h'(1)<0 és az (1,m/ $alpha$ ) intervallumban h''<0, így ebben az intervallumban h'<0. Mivel h(1)=0, ebből következik, hogy az (1,m/ $alpha$ ] intervallumban h<0. Az (m/ $alpha$ , $infty$ ) intervallumban h''>0, vagyis a h függvény konvex. 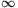Mivel h(m/ $alpha$ )<0 és $\lim\limits_\infty h=\infty$ , ebből következik, hogy létezik egy olyan $varrho$ >1 valós szám, hogy az (1, $varrho$ ) intervallumon h<0 és a ( $varrho$ , $infty$ ) intervallumon h>0.

Bármelyik esetről is legyen szó, ha h(t₂) $ge$ 0, akkor a teljes (t₂,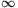 $infty$ ) intervallumban h $ge$ 0, azaz g' $le$ 0. Ezért a g függvény a [t₂,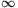 $infty$ ) intervallumban monoton fogy, és 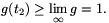$g(t_2)\ge\lim\limits_\infty g=1.$ Ha pedig h(t₂) $le$ 0, akkor az (1,t₂) intervallumban h $le$ 0, azaz g' $ge$ 0, tehát g monoton nő, és g(t₁) $le$ g(t₂). Ezzel az 1. lemmát igazoltuk.

A 2. lemma bizonyítása. Az állítást teljes indukcióval igazoljuk. Ha n=1, akkor csak x₁=m lehetséges, és az állítás semmitmondó. Tegyük fel, hogy n $ge$ 2, és kevesebb változó esetén az állítás igaz.

Az x₁,...,x_n számok között van m-nél nem nagyobb és nem kisebb is; a szimmetria miatt feltehetjük például, hogy x₁ $le$ m $le$ x₂. Jelöljük az m és az x₁x₂/m számok közül a kisebbiket y₁-gyel, a nagyobbikat y₂-vel. Ekkor x₁ $le$ y₁ $le$ y₂ $le$ x₂ és y₁y₂=x₁x₂. Ezért az 1. lemma alapján

(1)	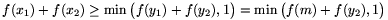$f(x_1)+f(x_2)\ge\min\big(f(y_1)+f(y_2),1\big)=\min\big(f(m)+f(y_2),1\big)$

Az y₂,x₃,...,x_n számok mértani közepe szintén m, ezért az indukciós feltevés alapján

(2)	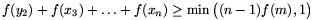$f(y_2)+f(x_3)+\dots+f(x_n)\ge\min\big((n-1)f(m),1\big)$

Ha f(x₁)+f(x₂)>1, akkor f(x₁)+...+f(x_n) $ge$ f(x₁)+f(x₂)>1, tehát az állítás igaz. Ha f(x₁)+f(x₂) $le$ 1, akkor (1) azt mondja, hogy f(x₁)+f(x₂) $ge$ f(m)+f(y₂). Ezt és (2)-t felhasználva,

f(x₁)+f(x₂)...+f(x_n) $ge$ f(m)+f(y₂)+f(x₃)+...+f(x_n) $ge$

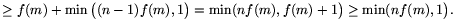
$\ge f(m)+\min\big((n-1)f(m),1\big)=\min(nf(m),f(m)+1\big)\ge\min(nf(m),1\big).$

Ezzel a 2. lemmát, egyben a feladat állítását is igazoltuk

A. 277. Legyen H₁ egy n-oldalú sokszög. Készítsük el a H₁, H₂, ..., H_n sokszögsorozatot a következőképpen. Ha H_k-t már elkészítettük, akkor H_k+1-et úgy kapjuk, hogy H_k csúcsait rendre tükrözzük a pozitív körüljárás szerinti k-adik szomszédjukra.

Bizonyítsuk be, hogy ha n prímszám, akkor a H₁ és H_n sokszögek hasonlók.

1. megoldás. A megoldás során, a kimondott segédállítások világosabb megfogalmazása érdekében az n-oldalú sokszögek helyett pont n-eseket fogunk használni.

Tetszőleges 0<k<n egész szám esetén jelöljük $tau$ _k-val azt a transzformációt, amelynek során egy pont n-esből úgy állítunk elő egy másik pont n-est, hogy mindegyik pontot tükrözzük a k-adik rákövetkezőjére. A transzformáció definícióját tetszőleges k egész számra is értelmezhetjük, ha k-t modulo n vizsgáljuk.

A feladat szerint H_k+1= $tau$ _k(H_k), és azt kell igazolnunk, hogy a $tau$ _n-1( $tau$ _n-2(... $tau$ ₂( $tau$ ₁(H₁))...)) n-szög hasonló a H₁-hez.

Először bebizonyítjuk, hogy a transzformációk felcserélhetők, azaz tetszőleges k,m egész számokra és P pont n-esre $tau$ _m( $tau$ _k(P))= $tau$ _k( $tau$ _m(P)). Legyenek P pontjai p₁, ..., p_n. Ekkor -- az indexeket modulo n értelmezve --

- a $tau$ _k(P) sokszög i-edik pontja 2p_i+k-p_i;

- a $tau$ _m(P) sokszög i-edik pontja 2p_i+m-p_i;

- a $tau$ _m( $tau$ _k(P)) sokszög i-edik pontja 2(2p_i+m+k-p_i+m)-(2p_i+k-p_i)=4p_i+m+k-2p_i+k-2p_i+m+p_i;

- a $tau$ _k( $tau$ _m(P)) sokszög i-edik pontja 2(2p_i+k+m-p_i+k)-(2p_i+m-p_i)=4p_i+m+k-2p_i+k-2p_i+m+p_i.

A $tau$ _m( $tau$ _k(P)) és a $tau$ _k( $tau$ _m(P)) pont n-es tehát ugyanaz.

A transzformációk felcserélhetőségéből következik, hogy a $tau$ ₁, $tau$ ₂, ..., $tau$ _n-1 transzformációkat tetszőleges sorrendben végrehajthatjuk, az eredmény mindig ugyanaz lesz.

Legyen H₁=(h₁,...,h_n) és H_n=(g₁,...,g_n). Mivel minden egyes transzformáció a pontokat egy-egy lineáris kombinációra cseréli ki, a g₁, ..., g_n pontok mindegyike a h₁, ..., h_n pontok egy-egy alkalmas lineáris kombinációjaként írható fel. Mivel pedig az indexek ciklikus cseréjére a transzformációsorozat szimmetrikus, az egyes kombinációk együtthatói egymásból ciklikus cserével kaphatók, azaz léteznek olyan a₀, a₁, ..., a_n-1 konstansok, hogy tetszőleges i esetén

(3)	g_i=a₀h_i+a₁h_i+1+...+a_n-1h_i+n-1.

Még azt is megmutatjuk, hogy a₁=a₂=...=a_n-1.

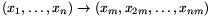Legyen tetszőleges 0<m<n egészre $pi$ _m az $(x_1,\dots,x_n)\to(x_m,x_{2m},\dots,x_{nm})$ permutáció. (Ez valóban permutáció, ha n prímszám.) A definíciót behelyettesítve ellenőrizhető, hogy tetszőleges k egész és P pont n-es esetén

$tau$ _k( $pi$ _m(P))= $pi$ _m( $tau$ _km(P)).

Ezt az azonosságot (n-1)-szer alkalmazva,

$tau$ _n-1( $tau$ _n-2(... $tau$ ₁( $pi$ _m(H₁))...))= $pi$ _m( $tau$ _(n-1)m( $tau$ _(n-2)m(... $tau$ _m(H₁)...))).

Mivel n prímszám, a $tau$ _m, $tau$ _2m, ..., $tau$ _(n-1)m transzformációk között $tau$ ₁, ..., $tau$ _n-1 mindegyike pontosan egyszer fordul elő. Ezért a jobboldalon $pi$ _m(H_n)=(g_m,g_2m,...,g_nm) áll.

A baloldalon a transzformációkat a $pi$ _m(H₁)=(h_m,h_2m,...,h_nm) sokszögre alkalmazzuk. A (3) azonosság szerint az eredményül kapott pont n-es i-edik tagja

a₀h_im+a₁h_(i+1)m+...+a_n-1h_(i+n-1)m.

Az eredményeket összegezve, tetszőleges i esetén

a₀h_im+a₁h_(i+1)m+...+a_n-1h_(i+n-1)m=

=g_im=a₀h_im+a₁h_im+1+...+a_n-1h_im+n-1.

A h_(i+1)m együtthatója a baloldalon a₁, a jobboldalon a_m, ezért a_m=a₁. Mivel ez minden 0<m<n-re igaz, a₁=a₂=...=a_n-1.

A H₁ és a H_n sokszög i-edik élvektora h_i+1-h_i, illetve g_i+1-g_i=(a₀-a₁)(h_i+1-h_i). Ezért a két sokszög hasonló, a hasonlóság aránya a₀-a₁.

2. megoldás. A feladatot komplex számok és az úgynevezett véges Fourier-transzformált segítségével oldjuk meg. A sokszögeket komplex számokból álló szám n-eseknek tekintjük. Hogy a későbbi számolás valamivel egyszerűbb legyen, helyezzük el H₁-et a komplex számsíkon úgy, hogy súlypontja a 0 legyen.

A szám n-esek tagjait indexeléssel fogjuk jelölni. Ha X egy szám n-est jelöl, akkor X_j fogja jelölni a j-edik elemét. Az indexelés mindig modulo n történik, például X_n=X₀ vagy X_-1=X_n-1.

A komplex szám n-esek körében értelmezzük a tagonkénti összeadást, kivonást és szorzást, továbbá a számmal való szorzást. Ezen kívül definiáljuk a szám n-esek véges Fourier-transzformáltját a következőképpen. Legyen 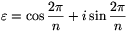$\varepsilon=\cos{2\pi\over n}+i\sin{2\pi\over n}$ az első n-edik komplex egységgyök. Az X szám n-es Fourier-transzformáltja az a $varphi$ (X) szám n-es, amelyre tetszőleges j esetén

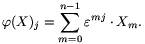
$\varphi(X)_j=\sum_{m=0}^{n-1}\varepsilon^{mj}\cdot X_m.$

A véges Fourier-transzformáltnak sok érdekes tulajdonsága és alkalmazása ismert, ezekről bővebben például Gács Péter és Lovász László Algoritmusok c. könyvében olvashatunk. Most a következőkre lesz szükségünk:

- Tetszőleges c számra és X szám n-esre $varphi$ (c^.X)=c^. $varphi$ (X).

- A Fourier-transzformált invertálható. Mint könnyen ellenőrizhető,

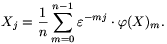
$X_j={1\over n}\sum_{m=0}^{n-1}\varepsilon^{-mj}\cdot\varphi(X)_m.$

Az 1. megoldáshoz hasonlóan legyen $tau$ _k az a transzformáció, amely során egy szám n-es mindegyik elemét tükrözzük a k-adik rákövetkezőjére, azaz

$tau$ _k(X)_j=2X_j+k-X_j.

A Fourier-transzformált és $tau$ _k definíciójából következik, hogy tetszőleges x szám n-esre

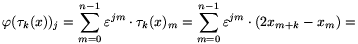
$\varphi(\tau_k(x))_j=\sum_{m=0}^{n-1}\varepsilon^{jm}\cdot\tau_k(x)_m=\sum_{m=0}^{n-1}\varepsilon^{jm}\cdot(2x_{m+k}-x_m)=$

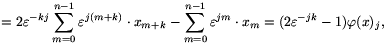
$=2\varepsilon^{-kj}\sum_{m=0}^{n-1}\varepsilon^{j(m+k)}\cdot x_{m+k}-\sum_{m=0}^{n-1}\varepsilon^{jm}\cdot x_m=(2\varepsilon^{-jk}-1)\varphi(x)_j,$

azaz

$varphi$ ( $tau$ _k(x))=(1,2 $varepsilon$ ^-k-1,2 $varepsilon$ ^-2k-1,...,2 $varepsilon$ ^-(n-1)k-1)^. $varphi$ (x).

Ezt minden 0<k<n-re alkalmazva,

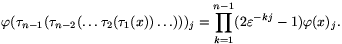
$\varphi(\tau_{n-1}(\tau_{n-2}(\dots\tau_2(\tau_1(x))\dots)))_j=\prod_{k=1}^{n-1}(2\varepsilon^{-kj}-1)\varphi(x)_j.$

Ha j=0, akkor 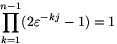$\prod_{k=1}^{n-1}(2\varepsilon^{-kj}-1)=1$ . Ha 0<j<n, akkor -- mivel n prímszám -- 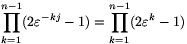$\prod_{k=1}^{n-1}(2\varepsilon^{-kj}-1)=\prod_{k=1}^{n-1}(2\varepsilon^k-1)$ . Jelöljük ezt a számot C-vel.

Azt kaptuk tehát, hogy

(4)	$varphi$ ( $tau$ _n-1( $tau$ _n-2(... $tau$ ₂( $tau$ ₁(x))...)))=(1,C,C,...,C)^. $varphi$ (x).

Tekintsük a $varphi$ (H₁) és a $varphi$ (H_n) szám n-eseket. A súlypont megválasztása miatt $varphi$ (H₁)₀=0, és ezért (4)-et a következő alakba is írhatjuk:

$varphi$ (H_n)= $varphi$ ( $tau$ _n-1( $tau$ _n-2(... $tau$ ₂( $tau$ ₁(H₁))...)))=C^. $varphi$ (H₁).

Ebből következik, hogy H_n=C^.H₁, vagyis H_n a H₁ 0 középpontú, C-szeres nagyítása.

Megjegyzés. A

p(t)=(t- $varepsilon$ )(t- $varepsilon$ ²)^.(t- $varepsilon$ ^n-1)=x^n-1+x^n-2+...+x+1

polinom felhasználásával

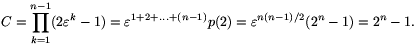
$C=\prod_{k=1}^{n-1}(2\varepsilon^k-1)=\varepsilon^{1+2+...+(n-1)}p(2)=\varepsilon^{n(n-1)/2}(2^n-1)=2^n-1.$

(Felhasználtuk, hogy n páratlan prímszám, és n(n-1)/2 osztható n-nel.)

Már regisztráltál?
Új vendég vagy?