 |
A 2001. novemberi B-jelű matematika feladatok megoldása |
A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.
B. 3492. Egy nxn-es táblázatba beírjuk sorban az 1, 2, ..., n2 számokat:
|
Minden sorból kiválasztunk egy-egy számot úgy, hogy semelyik kettő ne legyen ugyanabban az oszlopban.
Mik a kiválasztott számok összegének lehetséges értékei? (3 pont)
IMC 8, Prága, 2001
Megoldás. A táblázat i-edik sorának j-edik eleme (i-1)n+j. Bárhogyan választunk is ki n számot a táblázatból a kívánalomnak megfelelően, mind az i, mind a j értéke pontosan egyszer fogja felevenni az 1,2,...,n számok mindegyikét. Ezért a kiválasztott számok összege (függetlenül attól, hogy az n! különböző lehetőség közül milyen módon választottuk ki azokat)
\(\displaystyle \sum_{i=1}^n(i-1)n+\sum_{j=1}^nj=n{n(n-1)\over2}+{(n+1)n\over2}={n(n^2+1)\over2}\ .\)
A kiválasztott számok összegének egyetlen lehetséges értéke tehát \(\displaystyle {n(n^2+1)\over2}\).
B. 3493. Ketten a következő játékot játsszák. Egy kupacból, amelyben kezdetben páratlan darab gyufaszál van, felváltva vesznek el minden lépésben egy, két vagy három szál gyufát, amíg mind el nem fogy. Az nyer, akinél a végén páros számú gyufa van.
A kezdőnek, vagy ellenfelének van-e nyerő stratégiája? (5 pont)
Kvant
Megoldás. Jelölje a kupacban lévő gyufák számát k. Azt állítjuk, hogy ha k 8-cal osztva 1 maradékot ad, akkor a második játékosnak van nyerő stratégiája, minden egyéb esetben pedig a kezdő játékos tud nyerni, ha megfelelőképpen játszik. Legyen X(k) értéke 1 vagy 2 aszerint, hogy a kezdő vagy a második játékosnak van-e nyerő stratégiája. Hasonlóképpen legyen Y(k) értéke 1 vagy 2 aszerint, hogy a kezdő vagy a második játékosnak van-e nyerő stratégiája abban a játékban, amelynek feltételei megegyeznek a feladatban szereplőével, de az nyer, akinél a végén páratlan számú gyufa van. Könnyen ellenőrizhető, hogy Y(1)=X(3)=Y(3)=X(5)=X(7)=Y(7)=1 és X(1)=Y(5)=2. A megoldáshoz a következő állítást fogjuk indukcióval bizonyítani: ha k 4-gyel osztva 3 maradékot ad, akkor X(k)=Y(k)=1, ha k 8-cal osztva 1 maradékot ad, akkor X(k)=2 és Y(k)=1, végül ha k 8-cal osztva 5 maradékot ad, akkor X(k)=1 és Y(k)=2. Mint említettük, ez k=1,3,5,7 esetén így van, a továbbiakban tehát feltesszük, hogy k\(\displaystyle ge\)9, és az állítást 1,3,5,...,k-2 kezdeti gyufaszál esetén már igazoltuk.
Ha k 8-cal osztva 3 maradékot ad, akkor X(k-2)=2 az indukciós feltevés miatt. Ha tehát (az eredeti játékban) a kezdő játékos első lépésként 2 gyufaszálat vesz el, akkor a kupacban k-2 szál gyufa marad, és innentől kezdve bármit is csinál a második játékos, a kezdő alkalmazhatja a második játékos nyerő stratégiáját abban a játékban, amelyikben eredetileg k-2 szál gyufa volt, és ezzel biztosan nyeri a játékot, X(k)=1. Az is látszik ebből, hogy ha X(k-2)=1, tehát minden más esetben, a második játékos meg tudja akadályozni, hogy a kezdő nyerjen, amennyiben a kezdő 2 szál gyufát vesz el először. Ha tehát a kezdő játékosnak van nyerő stratégiája, az csak úgy kezdődhet, hogy az elején páratlan számú gyufát vesz el. Hasonló gondolatmenetet alkalmazva a másik játék esetében kapjuk azt, hogy Y(k)=1 ha k 8-cal osztva 7 maradékot ad.
Ha k 8-cal osztva 1 maradékot ad, és a kezdő játékos 2 szál gyufát vesz el először, akkor, mint azt láttuk, a második játékos biztosan meg tudja nyerni a játékot. Ha pedig 1 vagy 3 szál gyufát vesz el, akkor a második játékos megteheti azt, hogy 3, illetve 1 szál gyufát vegyen el. Mivel most Y(k-4)=2, ezek után a második játékosnak van nyerő stratégiája is arra, hogy a megmaradt k-4 gyufaszálból páratlan sokat gyűjtsön össze, és ezzel megnyerje az eredeti játékot. Bármit is csinál tehát a kezdő fél, a második tud úgy játszani, hogy a játék végére páros számú gyufája legyen, azaz X(k)=2. Hasonló gondolatmenetet alkalmazva a másik játék esetében kapjuk azt, hogy Y(k)=2 ha k 8-cal osztva 5 maradékot ad.
Ha k 8-cal osztva 5 maradékot ad, akkor X(k)=1. Valóban, ha az első játékos először 1 szál gyufát vesz csak el, és továbbra is megfelelő stratégiával játszik, akkor meg tudja nyerni a játékot. Ha ugyanis a második játékos ezután 1 szál gyufát vesz el, akkor a maradék k-2 gyufából az első játékos még páratlan sokat kell, hogy összegyűjtsön, és ezt Y(k-2)=1 miatt meg is tudja tenni. Hasonló a helyzet, ha a második játékos nem 1, hanem 3 szál gyufát vesz el, mert Y(k-4)=1 is igaz. Végül, ha a második 2 gyufát venne el, akkor válaszlépésként az első vegyen el megint csak egyet. Ekkor 2 gyufája van, k-4 gyufa maradt, és X(k-4)=2 miatt a kezdő követheti a második játékos nyerő stratégiáját abban a játékban, amelyik k-4 szál gyufával indul. Hasonló gondolatmenetet alkalmazva a másik játék esetében kapjuk azt, hogy Y(k)=1 ha k 8-cal osztva 1 maradékot ad.
Végül, ha k 8-cal osztva 7 maradékot ad, akkor ismét csak X(k)=1. Most az a jó, ha a kezdő játékos először 3 szál gyufát vesz el. Ha erre válaszként a második játékos 1 vagy 3 gyufát vesz el, akkor Y(k-4)=Y(k-6)=1 miatt a kezdő tud úgy játszani, hogy a megmaradt gyufákból páratlan számút gyűjtsön össze. Ha pedig a második játékos 2 szál gyufát venne el, akkor erre válaszul az első vegyen el 1-et, így 4 szál gyufája lesz, és X(k-6)=2 miatt tud úgy játszani, hogy a megmaradó k-6 szál gyufából páros számút gyűjtsön össze. Hasonló gondolatmenetet alkalmazva a másik játék esetében kapjuk azt, hogy Y(k)=1 ha k 8-cal osztva 3 maradékot ad.
B. 3494. Igazoljuk, hogy ha az ax3+bx2+cx+d=0 egyenletnek három különböző pozitív gyöke van, akkor bc<3ad. (4 pont)
Javasolta: Bakonyi Gábor, Budapest
Megoldás. Jelölje a polinom gyökeit u,v és w. Lévén a\(\displaystyle ne\)0, a gyökök és együtthatók közötti összefüggés alapján
\(\displaystyle -{b\over a}=u+v+w,\ {c\over a}=uv+vw+wu\ \ {\hbox{\rmés}}\ -{d\over a}=uvw\)
pozitív számok. Mivel u,v,w (és ennélfogva uv,vw,wu is) különböző pozitív számok, a számtani és mértani közepek közötti, esetünkben határozott egyenlőtlenséget alkalmazva a
\(\displaystyle {-b\over3a}\cdot{c\over3a}= {u+v+w\over3}\cdot{uv+vw+wu\over3\) (uvw)^{1/3}(uvvwwu)^{1/3}=uvw=-{d\over a}">
egyenlőtlenséget kapjuk. Ezt a -9a2 negatív számmal beszorozva az egyenlőtlenség iránya megváltozik, és éppen a feladat állításához jutunk.
B. 3495. Az ABCD téglalap oldalai AB=3, BC=2. P az AB oldalnak az a pontja, amelyre a PD egyenes érinti, mégpedig E-ben, a BC átmérőjű kört. A kör középpontján és E-n átmenő egyenes az AB oldalt Q-ban metszi. Mekkora a PQE háromszög területe? (3 pont)
Javasolta: Gerőcs László, Budapest
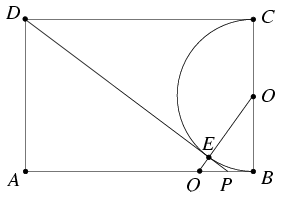
Megoldás. Jelöljük a BC oldal felezőpontját O-val. A DC, DE, PE és PB szakaszok egyaránt érintik a BC átmérőjű kört. Az egymást E-ben metsző DP és OQ szakaszok egymásra merőlegesek, akárcsak a téglalap szomszédos oldalai. Következésképpen a DEOC és OEPB négyszögek olyan deltoidok, melyekben a DEO, DCO, OEP és OBP szögek derékszögek. Ezért a COE szög mind a CDE, mind a BOE szöget 180o-ra egészíti ki, tehát a két deltoid hasonló. Ennek alapján EP/OE=EO/DE=EO/DC=EO/AB, tehát PB=EP=1/3. Innen kiszámolható az AP szakasz hossza is: AP=AB-BP=8/3. Végül az APD és EPQ derékszögű háromszögek hasonlóságából QE/EP=DA/AP=BC/AP alapján QE=1/4, a PQE háromszög területe pedig EP.EQ/2=1/24.
B. 3496. Az ABCD négyzet belsejében úgy vettük föl a P pontot, hogy AP:BP:CP=1:2:3. Mekkora az APB szög? (4 pont)
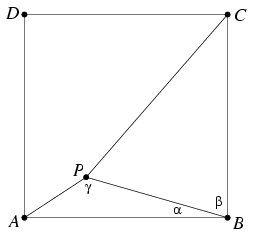
Megoldás. Jelölje az ABP, PBC és
APB szögeket rendre \(\displaystyle alpha\),\(\displaystyle beta\) és \(\displaystyle gamma\). Válasszuk az AP szakasz hosszát
egységnyinek és jelölje x az négyzet oldalainak hosszát. (Az
eredmény nyilván független az egység megválasztásától.) Mivel  +
+ =90o,
a trigonometrikus Pithagorasz-tétel alapján cos2
=90o,
a trigonometrikus Pithagorasz-tétel alapján cos2 +cos2\(\displaystyle beta\)=cos2
+cos2\(\displaystyle beta\)=cos2 +sin2\(\displaystyle alpha\)=1. Ezért, ha az ABP és
PBC háromszögek B-nél lévő szögeire a koszinusz-tételt
felírjuk, az alábbi összefüggést kapjuk:
+sin2\(\displaystyle alpha\)=1. Ezért, ha az ABP és
PBC háromszögek B-nél lévő szögeire a koszinusz-tételt
felírjuk, az alábbi összefüggést kapjuk:
\(\displaystyle \Bigl({x^2+3\over4x}\Bigr)^2+\Bigl({x^2-5\over4x}\Bigr)^2=1\ .\)
Innen
(x2+3)2+(x2-5)2=16x2,
ami x2=a helyettesítéssel
2a2-20a+34=0 alakra hozható, ahonnan a
értékére \(\displaystyle 5\pm2\sqrt{2}\) adódik. Nem lehet, hogy 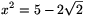 ,
mert ekkor \(\displaystyle (\sqrt{2}x)^2<9\) miatt a négyzet AC átlója rövidebb lenne
a PC szakasznál, vagyis P nem lehetne a négyzet
belsejében. Ezért \(\displaystyle x^2=5+2\sqrt{2}\). Végül az ABP háromszög P-nél
lévő szögére felírva a koszinusz-tételt,
,
mert ekkor \(\displaystyle (\sqrt{2}x)^2<9\) miatt a négyzet AC átlója rövidebb lenne
a PC szakasznál, vagyis P nem lehetne a négyzet
belsejében. Ezért \(\displaystyle x^2=5+2\sqrt{2}\). Végül az ABP háromszög P-nél
lévő szögére felírva a koszinusz-tételt,
\(\displaystyle \cos\gamma={5-x^2\over4}=-{1\over\sqrt{2}}\)
adódik, vagyis a keresett szög \(\displaystyle gamma\)=135o.
B. 3497. Az x valós számra {x}+{x-1}=1. Határozzuk meg
{x2001}+{x-2001}
értékét. (4 pont)
Javasolta: Besenyei Ádám, Tatabánya
Megoldás. Megmutatjuk, hogy minden i természetes számra x2i+1+x-(2i+1) egész szám. A feladat feltétele miatt ez i=0 esetén nyilván igaz. Az állítást teljes indukcióval bizonyítjuk. Legyen tehát k>0, és tegyük fel, hogy 0\(\displaystyle le\)i\(\displaystyle le\)k-1 esetén az állítást már igazoltuk. A binomiális tétel alkalmazásával rövid számolás és átrendezés után az
\(\displaystyle x^{2k+1}+x^{-(2k+1)}=(x+x^{-1})^{2k+1}- \sum_{i=1}^k{2k+1\choose i}(x^{2k+1-2i}+x^{2i-2k-1})\)
összefüggést nyerjük, ahol az egyenlőség jobboldalán az indukciós feltételből adódóan minden egyes zárójelen belül egész szám áll. Ezért az egyenlőség baloldalán is egész szám áll, ahogyan azt állítottuk.
Az elmondottakból következik, hogy {x2001}+{x-2001}
értéke is egész szám, tehát csakis 0 vagy 1 lehet. Ha 0 lenne, akkor
x2001 és reciproka is egész szám lenne, ami csak úgy
lehetséges, ha x2001=\(\displaystyle pm\)1, következésképpen x= 1, ellentétben az
{x}+{x-1}=1 feltétellel. A keresett érték
tehát 1.
1, ellentétben az
{x}+{x-1}=1 feltétellel. A keresett érték
tehát 1.
B. 3498. Az ABC háromszögben C-nél derékszög van. A hegyesszögek szögfelezői a szemközti oldalakat az M és az N pontban metszik. Legyen P az MN szakasz és a C-ből induló magasság metszéspontja. Bizonyítsuk be, hogy a CP hossza egyenlő a beírt kör sugarával. (4 pont)
Javasolta: Merényi Imre, Budapest
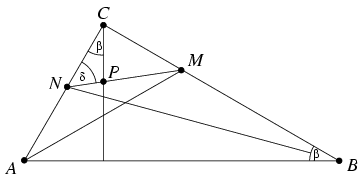
Megoldás. A háromszög a,b,c oldalaira
c2=a2+b2. Ha
M az a=BC, N pedig a b=AC
oldal pontja, akkor a szögfelező tételből
CM=ab/(b+c) és
CN=ab/(a+c). Jelölje a háromszög
B-nél lévő szögét \(\displaystyle beta\), ez megegyezik a CPN háromszög
C-nél lévő szögével. Az N-nél lévő szöget  -val jelölve
\(\displaystyle {\hbox{\rm
ctg}}\delta=CN/CM\). Ugyanerre a háromszögre a szinusz-tételt felírva
-val jelölve
\(\displaystyle {\hbox{\rm
ctg}}\delta=CN/CM\). Ugyanerre a háromszögre a szinusz-tételt felírva
\(\displaystyle {CN\over CP}={\sin(180^\circ-\beta-\delta)\over\sin\delta}= {\sin(\beta+\delta)\over\sin\delta}= \sin\beta{\cos\delta\over\sin\delta}+\cos\beta= {b\over c}\cdot{CN\over CM}+{a\over c},\)
\(\displaystyle {1\over CP}={b\over c\cdot CM}+{a\over c\cdot CN}= {1\over c}\Bigl({b^2+bc+a^2+ac\over ab}\Bigr)= {ac+bc+c^2\over abc}={a+b+c\over ab}\ ,\)
ami az ab=2T=r(a+b+c) képlet alapján éppen a beírt kör r sugarának reciproka. Így valóban CP=r.
B. 3499. Az x és y pozitív számok
mértani közepe g. Bizonyítsuk be, hogy ha g 3, akkor
3, akkor 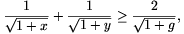 ha
pedig g
ha
pedig g 2,
akkor \(\displaystyle {1\over\sqrt{1+x}}+{1\over\sqrt{1+y}}\leq{2\over\sqrt{1+g}}\).
(5 pont)
2,
akkor \(\displaystyle {1\over\sqrt{1+x}}+{1\over\sqrt{1+y}}\leq{2\over\sqrt{1+g}}\).
(5 pont)
Megoldás. A z=1+x, v=1+y és h=1+g mennyiségek bevezetésével azt kell igazolnunk, hogy az
\(\displaystyle A={1\over\sqrt{z}}+{1\over\sqrt{v}}-{2\over\sqrt{h}}\)
kifejezés értéke nem negatív, ha h\(\displaystyle ge\)4, illetve nem pozitív, ha h 3 . A
pozitív
3 . A
pozitív
\(\displaystyle zvh\Bigl({1\over\sqrt{z}}+{1\over\sqrt{v}}+{2\over\sqrt{h}}\Bigr)\)
mennyiséggel szorozva látjuk, hogy az A kifejezés előjele megegyezik a
\(\displaystyle B=h(z+v+2\sqrt{zv})-4zv\)
kifejezés előjelével.
Mivel g az x és y számok mértani közepe,
(z-1)(v-1)=(h-1)2, ahonnan
z+v=zv-h2+2h, ezért 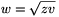 bevezetésével
bevezetésével
B=h(w2-h2+2h+2w)-4w2=(w-h)(h2+hw-4w-2h).
A számtani és mértani közepek közötti összefüggés alapján
x+y\(\displaystyle ge\)2g, z+v\(\displaystyle ge\)2h, tehát
w2=zv=h2-2h+z+v h2,
w\(\displaystyle ge\)h. Ezért
B, és így A előjele is megegyezik
C=h2-2h+(h-4)w
előjelével. Ha h\(\displaystyle ge\)4, akkor C\(\displaystyle ge\)h2-2h\(\displaystyle ge\)8, tehát A\(\displaystyle ge\)0, és egyenlőség csakis a
w=h, x=y esetben állhat fenn. Ha h
h2,
w\(\displaystyle ge\)h. Ezért
B, és így A előjele is megegyezik
C=h2-2h+(h-4)w
előjelével. Ha h\(\displaystyle ge\)4, akkor C\(\displaystyle ge\)h2-2h\(\displaystyle ge\)8, tehát A\(\displaystyle ge\)0, és egyenlőség csakis a
w=h, x=y esetben állhat fenn. Ha h 3, akkor
C=zv-z-v+(h-4)w
3, akkor
C=zv-z-v+(h-4)w w2-(z+v)-w, és itt
w2-(z+v)-w, és itt 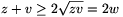 , vagyis C\(\displaystyle le\)w2-3w=w(3-w)
, vagyis C\(\displaystyle le\)w2-3w=w(3-w) w(3-h)\(\displaystyle le\)0. Ekkor tehát A
w(3-h)\(\displaystyle le\)0. Ekkor tehát A 0, és könnyű
ellenőrizni, hogy egyenlőség most is csak az x=y esetben
áll fenn.
0, és könnyű
ellenőrizni, hogy egyenlőség most is csak az x=y esetben
áll fenn.
B. 3500. Száz fiú és száz lány áll egy-egy sorban egymással szemben. Minden egyes fiú kiválaszt magának egy lányt (ugyanazt a lányt többen is választhatják) és egyenesen odamegy hozzá. Útközben a fiúk útvonalai nem keresztezik egymást. Ezután a fiúk visszaállnak a helyükre, most a lányok választanak, és most is teljesül, hogy miközben egyenesen odamennek a kiszemelt fiúhoz, az útvonalaik nem keresztezik egymást. Bizonyítsuk be, hogy van olyan lány és fiú, akik egymást választották. (4 pont)
Megoldás. Számozzuk meg a fiúkat és a lányokat is sorban
1-től 100-ig úgy, hogy az i-edik fiúval
(fi) szemben éppen az i-edik lány
(\(\displaystyle ell\)i) áll. Minden 1\(\displaystyle le\)i\(\displaystyle le\)100 esetén legyen  (i)=j, ha fi éppen
\(\displaystyle ell\)j-t választotta. Hasonlóképpen legyen
(i)=j, ha fi éppen
\(\displaystyle ell\)j-t választotta. Hasonlóképpen legyen 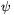 (i)=j
ha \(\displaystyle ell\)i éppen fj-t
választotta. Az, hogy a fiúk útvonalai nem keresztezik egymást, úgy
fogalmazható meg, hogy minden 1\(\displaystyle le\)i\(\displaystyle le\)j\(\displaystyle le\)100 esetén
(i)=j
ha \(\displaystyle ell\)i éppen fj-t
választotta. Az, hogy a fiúk útvonalai nem keresztezik egymást, úgy
fogalmazható meg, hogy minden 1\(\displaystyle le\)i\(\displaystyle le\)j\(\displaystyle le\)100 esetén  (i)\(\displaystyle le\)
(i)\(\displaystyle le\) (j), vagyis a
(j), vagyis a  függvény monoton
növekedő. Hasonlóképpen a
függvény monoton
növekedő. Hasonlóképpen a 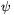 függvény, és így következésképpen a két
függvény kompozíciója is monoton növekedő.
függvény, és így következésképpen a két
függvény kompozíciója is monoton növekedő.
Mármost 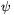 (
( (1))
(1)) 1 és
1 és 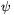 (
( (100))
(100)) 100. Ezért létezik 1 és 100 között egy legkisebb olyan
n egész szám, amelyre
100. Ezért létezik 1 és 100 között egy legkisebb olyan
n egész szám, amelyre 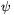 (
( (n))
(n)) n teljesül. Ha n=1, akkor
szükségképpen
n teljesül. Ha n=1, akkor
szükségképpen 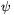 (
( (n))=
(n))=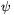 (
( (1))=1=n, egyébként pedig
(1))=1=n, egyébként pedig 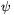 (
( (n-1))>n-1 miatt
(n-1))>n-1 miatt
n
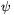 (
( (n-1))
(n-1))
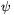 (
( (n))
(n)) n .
n .
Találtunk tehát egy olyan n értéket, amelyre 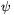 (
( (n))=n, ami pontosan azt jelenti, hogy az
n-edik fiú és a
(n))=n, ami pontosan azt jelenti, hogy az
n-edik fiú és a  (n)-edik lány egymást
választották.
(n)-edik lány egymást
választották.
B. 3501. Adottak a térbeli koordinátarendszerben az A(1, 1, 1) és a P(1, 1, 0) pontok. Forgassuk el az OA félegyenes körül pozitív irányban 60o-os szöggel a P pontot. Határozzuk meg az elforgatott pont koordinátáit. (4 pont)
Megoldás. Tekintsük az X(3,0,0), Y(0,3,0) és
Z(0,0,3) pontokat. Ezek egy szabályos háromszöget alkotnak,
melynek csúcsai illeszkednek az x+y+z=3 egyenletű
síkra, akárcsak az A pont, mely egyben az XYZ hároszög
középpontja is, hiszen mindhárom csúcstól 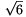 távolságra van. Az OA szakasz hossza pedig
távolságra van. Az OA szakasz hossza pedig 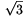 , a
Pithagorasz-tétel alapján tehát könnyen látható hogy OAX,
OAY és OAZ egybevágó derékszögű háromszögek. Azt is
mutatja ez az észrevétel, hogy az OA egyenes merőleges az XYZ
háromszög síkjára. Ha tekintjük az XY szakasz
F(3/2,3/2,0) felezőpontját és az AY szakasz
F'(1/2,2,1/2) felezőpontját, akkor könnyen ellenőrizhető, hogy
az AFF' háromszög szabályos. A feladatban szereplő elforgatás
tehát az F pontot F'-be viszi, és így az
, a
Pithagorasz-tétel alapján tehát könnyen látható hogy OAX,
OAY és OAZ egybevágó derékszögű háromszögek. Azt is
mutatja ez az észrevétel, hogy az OA egyenes merőleges az XYZ
háromszög síkjára. Ha tekintjük az XY szakasz
F(3/2,3/2,0) felezőpontját és az AY szakasz
F'(1/2,2,1/2) felezőpontját, akkor könnyen ellenőrizhető, hogy
az AFF' háromszög szabályos. A feladatban szereplő elforgatás
tehát az F pontot F'-be viszi, és így az 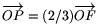 vektort pedig az
vektort pedig az
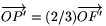 vektorba. A
keresett P' pont koordinátái tehát az F' pont megfelelő
koordinátáiból (1/3,4/3,1/3).
vektorba. A
keresett P' pont koordinátái tehát az F' pont megfelelő
koordinátáiból (1/3,4/3,1/3).

