Fizikából kitűzött gyakorlatok és feladatok
2001. november

Kérjük, olvassa el a versenykiírást.

Mérési feladat

M. 228. Ismeretes, hogy ha egy pohárban megkavarjuk a teát, a lesüllyedt tealevelek a pohár közepén gyűlnek össze egy kis kupacba (várakozásunkkal ellentétben, ugyanis a nagyobb sűrűségű anyagok általában kisodródnak a forgó folyadékban a tartály szélére). Mi a jelenség magyarázata? Végezzünk kísérletet a magyarázat igazolására! (6 pont)

Közli: Holics László, Budapest

Az elméleti versenyben kitűzött gyakorlatok és feladatok Az elméleti fizika feladatokra kapható pontszám a feladatok nehézségétől függ. Az 1-8. osztályosok versenyében minden hónapban a 3 legnagyobb, a 9-12. osztályosok versenyeiben minden hónapban az 5 legnagyobb pontszám számít be a pontversenybe.

P. 3466. Domború tükörbe nézve az orrunk aránytalanul nagyobbnak látszik, mint a fülünk. Miért? (3 pont)

Tarján Imre fizikaverseny, Szolnok

P. 3467. Pihenés nélkül kerékpározva két város között oda-vissza 6 óra a menetidő. Milyen messze van a két város egymástól, ha a vízszintes útszakaszokon 16 km/h, lejtőn felfelé 12 km/h, lejtőn lefelé pedig 24 km/h átlagsebességgel haladunk? (3 pont)

Közli: Kotormán Mihály, Debrecen

P. 3468. Hőszigetelt edényben 15 ^oC-os csapvíz van. Ebbe tesszük a mélyhűtőből kivett -15 ^oC-os jégkockákat. Lehet, hogy nem történik halmazállapotváltozás? Mikor olvad meg a jég egy része? Mikor olvad meg az összes jég? Mikor fagy meg az összes víz? (4 pont)

Közli: Szegedi Ervin, Debrecen

P. 3469.  Az ábrán látható T alakú merev test három egyforma rúdból áll, és a rudak csatlakozási pontjában a síkjukra merőleges vízszintes tengely körül elfordulhat. A jobb oldali rúd végén és a rudat 2:3 arányban osztó pontban rögzített kötelek egy-egy vízszintes, ékkel alátámasztott rudat tartanak. A felső rudat tartó ék az alsó rudat 3:2 arányban osztja. A felső rúd tömege m₁, az alsóé m₂, a felső rúdra helyezett test tömege pedig m₃. Mekkora tömegű testet kell a bal oldali rúd végén felfüggeszteni az egyensúly biztosításához? Adatok: m₁=2,5 kg, m₂=6,0 kg, m₃=7,5 kg.

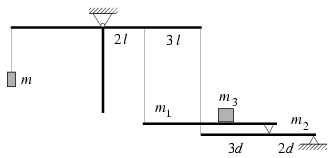
(5 pont)

Közli: Piacsek István, Sopron

P. 3470.  Egy lejtő végéhez az ábrán látható módon egy kiskocsi csatlakozik. A lejtőről h magasságból elengedett test a könnyen gördülő kiskocsi közepéig csúszik. (A lejtő és a test közötti súrlódás, valamint a kiskocsi kerekeinek tömege elhanyagolható.) Milyen magasból indítsuk a testet, hogy éppen a kiskocsi végénél álljon meg?

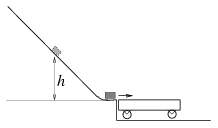
(4 pont)

Közli: Kiss Miklós, Gyöngyös

P. 3471. Vékony, de elég merev huzalt 0,6 m sugarú, 30^o meredekségű csavarvonal alakra hajlítunk, és úgy rögzítjük, hogy a csavarvonal tengelye függőleges legyen. Ezután a huzalra egy apró, átfúrt gyöngyöt fűzünk, amit egy adott pillanatban elengedünk. Mekkora sebességre gyorsul fel a gyöngy, ha a súrlódási együttható 0,5? (5 pont)

Közli: Szkladányi András, Baja (Mikola-verseny döntője, Sopron)

P. 3472. Egy hasábot és egy rugót egymáshoz erősítünk. A rugó végénél felfüggesztve a hasáb 1 másodperces rezgésidővel rezeg. Ezután a hasábot vízszintes asztalra tesszük, és egy függőleges fal felé lökjük úgy, hogy a rugó ütközőként elöl haladjon. A fallal ütközve a rugó összenyomódik, majd visszalöki a testet, amely éppen akkor áll meg, amikor a rugó teljesen nyújtatlanná válik. Mennyi idő telt el a rugó falhoz érésétől a visszalökött test megállásáig? (4 pont)

Közli: Honyek Gyula, Budapest

P. 3473. Milyen tömegszázalékos összetételű az a hidrogén-hélium gázelegy, amelynek izobár tágulásakor a környezettől felvett hő 70 %-a a belső energiát növeli? (4 pont)

Közli: Kopcsa József, Debrecen (Mikola Sándor fizikaverseny)

P. 3474.  Egy d hosszúságú szakasz végpontjaiban azonos nagyságú pozitív ponttöltések vannak. Mekkora az elektromos térerősség nagyságának és az elektromos potenciálnak a hányadosa a szakasz fölé emelt Thalész-kör egy szöggel jellemzett pontjában?

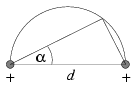
(4 pont)

Közli: Légrádi Imre, Sopron

P. 3475.  Az ábrán látható vékony, függőleges szigetelő rúd alsó végén levő ütközőn egy m=10^-4 kg tömegű, Q₁ töltésű gyöngy nyugszik. Felette h₀=20 cm távolságban egy ugyancsak m tömegű, Q₂ töltésű gyöngy lebeg. Egy adott pillanatban az alsó gyöngyöt megpöcköljük, ez ekkor v₀=2 m/s sebességgel elindul felfelé. Legfeljebb mennyire közelíti meg az első gyöngy a felsőt? (A gyöngyök súrlódásmentesen csúszhatnak a rúdon.)

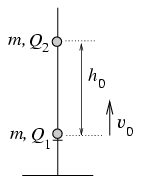
(6 pont)

Közli: Kiss Láó, Budapest (Egyetemi felvételi feladat alapján)

P. 3476. Homogén mágneses térben körpályán kering egy elektron. Lehet-e nagyobb az elektron mozgása által keltett mágneses indukcióvektor értéke a kör középpontjában, mint a homogén mágneses teret jellemző indukcióvektor? (5 pont)

Közli: Varga István, Békéscsaba (Bay Zoltán fizikaverseny, Sarkad)

P. 3477. Homogén, vékony lécből a, b és c oldalélű háromszög alakú keretet állítunk össze. A léckeret össztömege m. Mekkora a keret tehetetlenségi nyomatéka a tömegközéppontján átmenő, a háromszög síkjára merőleges tengelyre vonatkozóan? (5 pont)

Közli: Gnädig Péter, Budapest

A fizika feladatok megoldásai a következő címekre küldhetők:

KöMaL Szerkesztőség
Budapest 112, Pf. 32.  1518

megoldas@komal.elte.hu (Az interneten keresztül történő beküldésről olvassa el tájékoztatónkat)

A beküldési határidő: 2001. december 11.

Pontversenyen kívüli feladat. Száz éve (1901. szept. 29-én) született Enrico Fermi, Nobel-díjas olasz fizikus, aki mestere volt a nehéz problémák becsléseken alapuló, közelítő megoldásának. A legmeglepőbb kérdéseket sokan ma is Fermi-kérdéseknek nevezik. Álljon itt néhány:

a) Hány zongorahangoló lehet Chicagóban?

b) Mennyit fog sietni vagy késni az óránk, ha felvisszük egy hegyre?

c) Mekkora gravitációs vonzóerőt gyakorol egymásra az a férfi és nő, akik egymást átölelve ülnek egy padon?

Az első két kérdés magától Fermitől származik, a harmadik egy, már azóta született ,,Fermi-probléma''.

Közli: Radnai Gyula, Budapest

Olimpiai levelezés A feladat vázlatos megoldása vagy végeredménye 1 hónapon belül elektronikus (esetleg hagyományos) levélben küldhető be a gnadig@komal.elte.hu címre (illetve a Szerkesztőségbe). Minden levélíró néhány napon belül névre szóló választ kap, melyből megtudhatja, hogy jó-e a megoldása, vagy ha nem, hol hibázott és hogyan léphetne tovább.

OLI. 3. n darab egyforma rugalmas golyót fonalakra felfüggesztünk úgy, hogy egymással érintkezve egy egyenes mentén helyezkedjenek el. A sor végén egyszerre nekik ütközik k darab ugyanilyen golyó, mindegyikük sebessége v₀. Hány darab golyó fog elpattanni a sor másik végéről? Mekkora lesz a sebességük? (Feltételezhetjük, hogy valamennyi test egy egyenes mentén mozog.)