A 2001. decemberi B-jelű matematika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

B.3502. Az ABC hegyesszögű háromszögben az AB átmérőjű félkör a C-ből induló magasságot C₁-ben, a BC átmérőjű félkör az A-ból induló magasságot A₁-ben metszi. Bizonyítsuk be, hogy BC₁=BA₁. (3 pont)

Megoldás. Jelölje a C-ből induló magasságvonal talppontját M_c, az AB oldal felezőpontját pedig F. A szokásos jelölésekkel M_cB=asin$\displaystyle beta$, ezért M_cF=|asin$\displaystyle beta$-c/2|. A Pithagorasz-tételt az M_cFC₁ (esetleg elfajuló) és M_cBC₁ derékszögű háromszögekre alkalmazva

$\displaystyle M_cC_1^2=FC_1^2-M_cF^2=\Bigl({c\over2}\Bigr)^2-\Bigl(a\sin\beta-{c\over2}\Bigr)^2=-a^2\sin^2\beta+ac\sin\beta\ ,$

BC₁²=M_cB²+M_cC₁²=(asin$\displaystyle beta$)²+(-a²sin²$\displaystyle beta$+acsin$\displaystyle beta$)=acsin$\displaystyle beta$ .

A feladat szimmetriáját felhasználva ugyanígy BA₁²=acsin$\displaystyle beta$ is igaz, tehát valóban $\displaystyle BC_1=BA_1=\sqrt{ac\sin\beta}$.

B.3503. Adottak az a, b, c, d és f szakaszok. Tegyük fel, hogy létezik olyan négyszög, melynek egymást követő oldalai a, b, c, d, az a és c oldalak felezőpontját összekötő szakasz hossza pedig f. Szerkesszünk ilyen négyszöget. (4 pont)

Megoldás. Jelölje a szerkesztendő négyszög csúcsait pozitív körüljárási irány szerint A,B,C és D, ahol AB=a, BC=b, CD=c, DA=d, az AB,CD oldalak F,G felezőpontjaira pedig FG=f. A C,G,D pontokat F-re tükrözve kapjuk a C',G',D' pontokat. Ha a C'D szakasz felezőpontját H-val jelöljük, akkor $\displaystyle \overrightarrow{GD}=\overrightarrow{FH}=\overrightarrow{G'C'}$ miatt AC'=b, DC'=2f, FA=a/2 és FH=c/2. Ha a feladatnak van megoldása, akkor szükségképpen létezik az esetleg elfajuló ADC' háromszög, melynek oldalai d,b és 2f. Ez a háromszög csak a b+d=2f esetben lehet elfajuló.

Tegyük fel először, hogy ez a helyzet. Jelölje az AH szakasz hosszát h. Ha h=0, akkor b=d=f és szükségképpen a=c is teljesül a szerkeszthetőség miatt, ezért végtelen sok különböző paralelogramma a feladat megoldása, melyet könnyen megszerkeszthetünk, ha rögzítjük a BAD szöget, melynek nagysága tetszőleges 0 és $\displaystyle pi$ közötti érték lehet. Ha A$\displaystyle ne$H, akkor az AFH esetleg elfajuló háromszög a/2,c/2,h oldalaira kell hogy teljesüljön a háromszög egyenlőtlenség gyengített formája, mely esetben az A,D pontokat rögzítve a C' és H pontok helyzete meghatározott és így az F pont könnyen szerkeszthető: ha az AFH háromszög elfajuló, akkor F helye egyértelműen meghatározott, ellenkező esetben pedig két lehetőséget kell megvizsgálnunk aszerint, hogy F az AH egyenes melyik oldalára esik. F ismeretében pedig B és C már egyértelműen meghatározott, (csak nem biztos, hogy pozitív körüljárású ABCD négyszöghöz jutunk): B helyét $\displaystyle \overrightarrow{AB}=2\overrightarrow{AF}$, C helyét pedig $\displaystyle \overrightarrow{BC}=\overrightarrow{C'A}$ alapján tudjuk egyszerűen kijelölni.

Most tegyük fel, hogy az ADC' háromszög nem elfajuló, és rögzítsük ezt a háromszöget, mind a kétféle lehetséges körüljárási irányt megengedve. Ezután F pont és így maga a négyszög is az előbb ismertetett módon szerkeszthető, annyi különbséggel, hogy most a kétféle körüljárás miatt 2 (ha az AFH háromszög elfajuló) vagy 4 (egyébként) lehetőséget kell megvizsgálnunk. Megjegyezzük, hogy a szerkesztési adatok megválaszthatók úgy, hogy bármelyik körüljárási irányt rögzítve az ADC' háromszögre, a feladatnak legyen megoldása.

B.3504. Jelölje S(n) a tízes számrendszerben felírt n szám jegyeinek az összegét, U_k=11...1 pedig a k darab egyessel felírt számot. Keressük meg azokat a k értékeket, amelyekre S(U_k²)=(S(U_k))². (4 pont)

Megoldás. Mivel S(U_k)=k, azt kell meghatároznunk, hogy mely k értékekre teljesül S(U_k²)=k². Ha k$\displaystyle le$9, akkor ez teljesül, hiszen ekkor S(U_k²)=1+2+...+k+(k-1)+...+1=k². Megmutatjuk, hogy ha k$\displaystyle ge$10, akkor S(U_k²)<k².

Először is, S(U₁₀²)=82<10². Az S(m+n)$\displaystyle le$S(m)+S(n) egyenlőtlenség ismételt alkalmazásával pedig k$\displaystyle ge$10 esetén

$\displaystyle S(U_k^2)=S(U_{10}U_k+\sum_{i=10}^{k-1}10^iU_k)\le S(U_{10}U_k)+(k-10)S(U_k)\le$

$\displaystyle le$S(U₁₀²)+(k-10)S(U₁₀)+(k-10)S(U_k)=k²-18 .

Most már csak annak igazolása van hátra, hogy tetszőleges m,n természetes számokra S(m+n)$\displaystyle le$S(m)+S(n). Ez könnyen ellenőrizhető abban az esetben, ha m és n egyjegyű számok. Ha pedig legfeljebb t-jegyű számokra már igazoltuk az állítást, akkor legyen m=a10^t+M, n=b10^t+N, ahol a,b egyjegyű számok, M,N pedig legfeljebb t-jegyű számok. Ha M+N is legfeljebb t-jegyű szám, akkor S(m+n)=c+S(M+N), ahol c=a+b vagy c=a+b-9, attól függően, hogy a+b$\displaystyle le$9 vagy a+b$\displaystyle ge$10. Ha pedig M+N jegyeinek száma t+1, akkor S(m+n)=c+S(M+N), ahol c=a+b vagy c=a+b-9, attól függően, hogy a+b$\displaystyle le$8 vagy a+b$\displaystyle ge$9. Mindenesetre

S(m+n)=c+S(M+N)$\displaystyle le$a+b+S(M)+S(N)=S(m)+S(n) ,

vagyis az állítás érvényessége ilyen módon kiterjeszthető azokra a számokra is, melyek legfeljebb t+1 számjegyből állnak.

B.3505. Egy szabályos nyolcszöget paralelogrammákra osztunk fel. Bizonyítsuk be, hogy a paralelogrammák között van téglalap. (5 pont)

Megoldás. Válasszuk ki a nyolcszög két szemközti oldalát, legyenek ezek a és b. Legyen P₁ egy olyan paralelogramma a felosztásból, amelynek valamely a₁ oldala illeszkedik az a oldalra. P₁-nek ezzel szemközti oldalát jelölje b₁. Kell lennie olyan P₂ paralelogrammának is, amelynek egyik a₂-vel jelölt oldala olyan, hogy a₂-nek és b₁-nek a metszete egy nem egy pontból álló s₁ szakasz. P₂-nek a₂-vel szemben lévő oldalát b₂-vel jelölve megállpíthatjuk, hogy b₂ közelebb van a b oldal egyneséhez, mint b₁. Folytassuk ezt az eljárást, amíg csak lehet. Ilyen módon különböző paralelogrammáknak olyan P₁,P₂,...,P_m sorozatához jutunk, hogy minden i-re a P_i paralelogramma b_i oldalának és a P_i+1 paralelogramma a_i+1 oldalának közös része egy nem elfajuló s_i szakasz, mely párhuzamos az a,b oldalakkal. Ha ezt a sorozatot már nem tudjuk kibővíteni (már pedig egy idő után nem tudjuk, hiszen csak véges sok, a felosztásban szereplő paralelogramma közül választhatunk), az csak úgy lehet, hogy az utolsó paralelogramma b_m oldala illeszkedik a nyolcszög b oldalára. Az s₀=a₁,s_m=b_m jelölésket is bevezetve, legyen i=0,1,...,m esetén F_i az s_i szakasz felező pontja. Ekkor az s=F₀F₁...F_m töröttvonal összeköti a nyolcszög a és b oldalának egy-egy pontját úgy, hogy az F_i-1F_i szakasz végpontjaitól eltekintve végig a P_i paralelogramma belsejében halad. Legyen c és d a nyolcszögnek a-ra és b-re merőleges oldalai, és készítsünk el az előbbi eljárás mintájára egy Q₁,Q₂,...,Q_n paralelogramma-sorozatot, ahol most a Q_i megfelelő oldalait c_i és d_i jelöli, c_i+1 és d_i metszete a G_i felezőpontú t_i szakasz, és a t=G₀G₁...G_n töröttvonal összeköti a nyolcszög c és d oldalának egy-egy pontját úgy, hogy az G_i-1G_i szakasz végpontjaitól eltekintve végig a Q_i paralelogramma belsejében halad. A konstrukcióból adódik, hogy az s és t töröttvonalak a nyolcszög belsejében valamely X pontban metszik egymást. Az s_i és t_j szakaszok nem metszhetik egymást, különben a P_i és Q_j paralelogrammák egymásba nyúlóak lennének. Ezért X a P₁,...,P_m,Q₁,...,Q_n paralelogrammák közül valamelyiknek belső pontja. Az általánosság megszotítása nélkül feltehetjük, hogy X a P_i belsejében helyezkedik el. Mivel egyben valamelyik Q_j-nek is pontja, és a paralelogrammák nem nyúlnak egymásba, ez csak úgy lehetséges, ha P_i megegyezik Q_j-vel. Ekkor azonban P_i=Q_j olyan paralelogramma, melynek oldalai rendre az a,c,b,d szakaszokkal párhuzamosak. A felosztásban szereplő P_i paralelogramma tehát téglalap.

B.3506. Az f polinomra teljesül, hogy f(x²+1)-f(x²-1)=4x²+6. Határozzuk meg az f(x²+1)-f(x²) polinomot. (4 pont)

Megoldás. A keresett polinomot jelölje p, világos, hogy p-ben csak páros fokú tagok szerepelnek. Legyen ennek megfelelően q az a polinom, amelyre q(x²)=p(x). Az y=x² helyettesítéssel észrevehetjük, hogy minden y$\displaystyle ge$0 esetén

q(y)+q(y-1)=(f(x²+1)-f(x²))+(f(x²)-f(x²-1))=4x²+6=4y+6 .

Az r(t)=q(t)+q(t-1)-4t-6 polinomnak ezért végtelen sok gyöke van, r=0. Az s(t)=q(t)+q(t-1) polinom megegyezik tehát a 4t+6 polinommal. Mivel s főegyütthatója éppen q főegyütthatójának kétszerese, leolvasható innen, hogy q(t)=2t+b alakú. Ekkor s(t)=4t+2b-2, ahonnan b=4 adódik. A keresett polinom tehát p(x)=q(x²)=2x²+4.

B.3507. Legyen f(x) egész együtthatós polinom, p és q pedig relatív prímek, q0. Bizonyítsuk be, hogy ha p/q gyöke az f-nek, akkor f(k) minden k egészre osztható p-kq-val. Igaz-e az állítás megfordítása? (4 pont)

Megoldás. Legyen f(x)=a_nxⁿ+a_n-1x^n-1+...+a₁x+a₀, és tekintsük az

$\displaystyle A(k)=q^n\Bigl(f(k)-f({p\over q})\Bigl)=\sum_{i=0}^na_iq^{n-i}\Bigl((kq)^i-p^i\Bigr)$

kifejezést. Leolvasható, hogy A(k) értéke minden k egész esetén olyan egész szám, amely osztható (kq-p)-vel. Ha p/q gyöke f-nek, akkor ennek megfelelően A(k)=qⁿf(k) osztható (p-kq)-val. Megmutatjuk, hogy qⁿ és p-kq bármilyen k egész szám esetén relatív prímek; ebből az állítás azonnal következik. Ehhez tegyük fel, hogy egy t prímszám osztója qⁿ-nek és (p-kq)-nak is. Ekkor t osztója q-nak, következésképpen p-nek is. Ilyen t prímszám tehát nem létezik, qⁿ és p-kq valóban relatív prímek.

Az állítás megfordításához tegyük fel, hogy minden k egészre f(k) osztható (p-kq)-val, tehát (kq-p)-vel is. Ekkor minden k egészre a C=qⁿf(p/q)=qⁿf(k)-A(k) egész szám is osztható (kq-p)-vel. Mivel q$\displaystyle ne$0, ez azt jelenti, hogy C-nek tetszőlegesen nagy abszolút értékű osztói is vannak, ami csak úgy lehet ha C=0. Ismét a q$\displaystyle ne$0 feltételre hivatkozva kapjuk, hogy f(p/q)=0. Megállapíthatjuk tehát, hogy az állítás megfordítása is igaz.

B.3508. Az ABC és az A₁B₁C₁ háromszögek tengelyesen tükrös helyzetűek. Húzzunk párhuzamost A₁-en keresztül BC-vel, B₁-en keresztül AC-vel, végül C₁-en keresztül AB-vel. Bizonyítsuk be, hogy ez a három egyenes egy ponton halad át. (4 pont)

Megoldás. Az AB egyenes pontosan akkor párhuzamos az A₁C₁egyenessel, ha AC párhuzamos A₁B₁-gyel, és ekkor a három egyenes az A₁ pontban metszi egymást. Azt is könnyű megállapítani, hogy a három egyenes közül bármelyik kettő csak ebben az esetben metszheti egymást az A₁ pontban. Feltehetjük tehát hogy az ABC hároszög egyik oldala sem párhuzamos az A₁B₁C₁ háromszög egy nem neki megfelelő oldalával.

Jelölje a szóban forgó egyeneseket rendre e_A, e_B, e_C, közülük nyilván bármelyik kettő metszi egymást. Jelölje P az e_B és e_C egyenesek metszéspontját, a fenti feltevésünk miatt ez a pont B₁-től és C₁-től is különbözik. Irányított szögekkel modulo 2$\displaystyle pi$ számolva látszik, hogy a B₁PC₁ szög vagy megegyezik a CAB=B₁A₁C₁ szöggel, vagy annál $\displaystyle pi$-vel nagyobb (kisebb). A kerületi szögek tétele alapján tehát P az A₁B₁C₁ háromszög köré írt körön helyezkedik el, és feltevésünk miatt különbözik a háromszög csúcsaitól. Az e_B egyenes tehát a B₁ és P pontokban, míg az e_C egyenes a C₁ és P pontokban metszi a körülírt kört. Hasonló gondolatmenettel kapjuk, hogy az e_A és e_C egyenesek Q metszéspontja is a körülírt kör C₁-től különböző pontja. Ezért szükségképpen Q=P, a három egyenes mindegyike áthalad a P ponton.

B.3509. Bizonyítsuk be, hogy ha 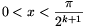, akkor

$\displaystyle {1\over\sin2x}+{1\over\sin4x}+\dots+{1\over\sin2^kx}<\ctg x.$

(3 pont)

Javasolta: Balogh János, Kaposvár

Megoldás. Ha k=0, akkor a baloldalon álló B(x) kifejezés üres összeg, ami 0-val egyenlő, a jobboldalon pedig pozitív szám áll. Az állítás tehát igaz k=0 esetén. Teljes indukcióval bizonyítunk. Tegyük fel ennek megfelelően, hogy k$\displaystyle ge$1 és az állítást k-1 esetén már igazoltuk. Ekkor \(\displaystyle 0$\displaystyle B(x)<{1\over{\sin2x}}+{\hbox{\rm ctg}}2x={1+\cos2x\over\sin2x}={2\cos^2x\over2\sin x\cos x}={\hbox{\rm ctg}}x\ ,$

amint azt bizonyítani kívántuk.

B.3510. Az ABCD tetraéder csúcsain keresztül fektessünk a szemközti lapokkal párhuzamos síkokat. Ez a négy sík egy újabb tetraédert határoz meg. Bizonyítsuk be, hogy A, B, C és D az így kapott tetraéder lapjainak a súlypontjai. (3 pont)

Megoldás. Tekintsük az $\displaystyle \overrightarrow{AA'}=\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}$, $\displaystyle \overrightarrow{BB'}=\overrightarrow{BA}+\overrightarrow{BC}+\overrightarrow{BD}$, $\displaystyle \overrightarrow{CC'}=\overrightarrow{CA}+\overrightarrow{CB}+\overrightarrow{CD}$ és $\displaystyle \overrightarrow{DD'}=\overrightarrow{DA}+\overrightarrow{DB}+\overrightarrow{DC}$ vektorokat. Azt állítjuk, hogy az A', B', C' és D' pontok az új tetraéder csúcspontjai. Ezt szimmetria okok miatt elég az A' pontra igazolni. Mivel az $\displaystyle \overrightarrow{AC}+\overrightarrow{AD}$ vektor párhuzamos az ACD síkkal, az A' pont illeszkedik a B ponton keresztül ezen síkkal párhuzamosan fektetett síkra. Ugyanígy látható, hogy az A' pont illeszkedik a C és D pontokon keresztül rendre az ABD, illetve ABC lapokkal párhuzamos síkokra. A' tehát valóban e három sík metszéspontja.

Most megmutatjuk, hogy D az A'B'C' háromszög súlypontja. Valóban,

$\displaystyle \overrightarrow{DA'}+\overrightarrow{DB'}+\overrightarrow{DC'}=(\overrightarrow{AB}+\overrightarrow{AC})+(\overrightarrow{BA}+\overrightarrow{BC})+(\overrightarrow{CA}+\overrightarrow{CB})={0}\ ,$

ami úgy is megfogalmazható, hogy tetszőleges O pontra

$\displaystyle \overrightarrow{OD}=\overrightarrow{OD}+3(\overrightarrow{DA'}+\overrightarrow{DB'}+\overrightarrow{DC'})={1\over3}(\overrightarrow{OA'}+\overrightarrow{OB'}+\overrightarrow{OC'})\ .$

Hasonlóképpen igazolható, hogy az A, B és C pontok rendre a B'C'D', A'C'D' és A'B'D' háromszögek súlypontjai.

B.3511. Az a, b, c, d nemnegatív számokra a1, a+b5, a+b+c14 és a+b+c+d30. Bizonyítsuk be, hogy 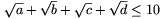. (5 pont)

Megoldás. Megmutatjuk, hogy az $\displaystyle S=\sqrt a+\sqrt b+\sqrt c+\sqrt d$ kifejezésnek az adott feltételek mellett maximális értéke 10, és S=10 pontosan akkor teljesül, ha a=1,b=4,c=9 és d=16. Ehhez először a következő állítást igazoljuk: Ha 0$\displaystyle le$x<y$\displaystyle le$z<v és x+v=y+z=K, akkor $\displaystyle \sqrt{y}+\sqrt{z$\sqrt{x}+\sqrt{v}">. Valóban, azonos átalakításokkal látszik, hogy az egyenlőtlenség sorra ekvivalens a $\displaystyle K+2\sqrt{yz$K+2\sqrt{xv}">, yz>xv, y(K-y)>x(K-x), (y-x)(K-y-x)>0 egyenlőtlenségekkel. Ez utóbbi azonban nyilvánvaló, hiszen y>x és K=y+z>y+x.

Tegyük fel tehát először is, hogy a,b,c,d kielégítik a feltételeket és d$\displaystyle ne$16. Feltehetjük, hogy a+b+c+d=30, ellenkező esetben ugyanis d értékét növelhetnénk a,b,c értékét változatlanul hagyva úgy, hogy a feltételek továbbra is teljesülnek, és S értéke eközben növekszik. Ha az így nyert számnégyesre továbbra is d$\displaystyle ne$16, akkor a harmadik és a negyedik feltétel egybevetésével látszik, hogy d>16 és a+b+c<14. Legyen most a₁=a, b₁=b, c₁=14-a-b$\displaystyle le$14 és d₁=16, ekkor c₁+d₁=c+d=30-a-b, és így a fenti segédállítás értelmében $\displaystyle \sqrt{c_1}+\sqrt{d_1$\sqrt{c}+\sqrt{d}">, $\displaystyle S_1=\sqrt{a_1}+\sqrt{b_1}+\sqrt{c_1}+\sqrt{d_1$S">. Tegyük fel most, hogy itt c₁$\displaystyle ne$9. Az előbbi gondolatmenethez hasonló módon először is feltehetjük, hogy a₁+b₁+c₁=14, máskülönben c₁ értékét növelhetnénk úgy, hogy a feltételek továbbra is teljesülnek. Legyen ekkor a₂=a₁, b₂=5-a₁, c₂=9 és d₂=d₁=16. Ekkor az a₂,b₂,c₂,d₂ számnégyesre továbbra is teljesülnek a feltételek, c₂=9, d₂=16 és $\displaystyle S_2=\sqrt{a_2}+\sqrt{b_2}+\sqrt{c_2}+\sqrt{d_2$S">. Ezt az eljárást még kétszer megismételve a következő eredményre jutunk: Ha a feltételeket kielégítő a,b,c,d számnégyes különbözik az 1,4,9,16 négyestől, akkor az a₄=1, b₄=4, c₄=9, d₄=16 számnégyesre teljesülnek a feltételek, és $\displaystyle 10=\sqrt{a_4}+\sqrt{b_4}+\sqrt{c_4}+\sqrt{d_4$S">, ami állításunkat igazolja.