Solutions for theoretical problems in Physics December, 2001

In this page only the sketch of the solutions are published; in some cases only the final results. To achieve the maximum score in the competition more detailed solutions needed.

P. 3478. Estimate how much work you do while you reach a proper press-up position from lying. (3 points)

Solution. W\(\displaystyle approx\)100-200 J.

P. 3479. Hydrogen gas is kept streaming through a tube while it is cooled by water surrounding the tube. The temperature of the incoming gas is 60 C^o and that of the outgoing gas is 30 C^o. The capacity of the cooler tank is 60 liter and the water in it is completely changed in every hour. The initial temperature of the cooling water is 10 C^o and it is 20 C^o when it is changed. What is the amount of the gas in kgs that goes through the tube in one hour? (4 points)

Solution.

m_hydrogen=5.9 kg.

P. 3480. From a 5000 km radius planet a rocket is launched at the first cosmic velocity in a direction at a 60^o angle to the vertical direction. What is the maximum height the rocket can reach? (5 points)

Solution. h=Rcos\(\displaystyle alpha\)=2500 km.

P. 3481. What is the relation between the temperature and the swing period of a physical pendulum made of a homogeneous material? (4 points)

Solution.

\(\displaystyle {\Delta T\over T}={1\over2}\alpha\Delta t.\)

P. 3482. On the middle one of three thin concentric spherical metal shells of radius R there is Q electric charge. The inner spherical shell of radius 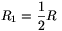and the outer spherical shell of radius 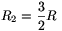are earthed.

a) What is the amount of the electric charge on the earthed spherical shells?

b) Plot the electric field strength versus the distance from the centre. (5 points)

Solution.

\(\displaystyle E(r)=\cases{-k{\displaystyle1\over\displaystyle4}{\displaystyle Q\over\displaystyle r^2},{\rm if\ }{1\over2}R

P. 3483. In the connection shown in the figure the switch K is open and the capacitor is uncharged. Then we close the switch and let the capacitor charge up to the maximum and open the switch again. Determine the values indicated by the ammeter

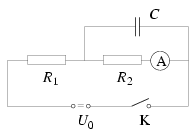
a) directly after closing the switch;

b) a long time after the switch was closed;

c) directly after reopening the switch;

U₀=30 V, R₁=10 k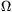, R₂=5 k\(\displaystyle Omega\).) (4 points)

Solution. a) After closing the switch I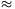0.

b) After a long time

\(\displaystyle I={U_0\over R_1+R_2}=2~\rm mA.\)

c) After reopening the switch I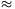2 mA.

P. 3484. What should be the capacity of the adjustable capacitor shown in the figure so that the voltmeter indicates the highest voltage? (5 points)

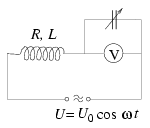
Solution. The voltage of the capacitor is

\(\displaystyle U_C={I\over\omega C}={U_0\over\sqrt{R^2\omega^2C^2+(1-\omega^2LC)^2}}.\)

This function has a maximum at

\(\displaystyle C={1\over L\omega^2+R^2/L}.\)

P. 3485. The Sun attracts the Earth with a lot greater force then the Moon does.

a) What is the ratio of the two forces?

b) What is the explanation for the fact that despite this the tidal effect of the Moon is a few times bigger than that of the Sun. (5 points)

Solution. a)

\(\displaystyle {F_{\rm Sun}\over F_{\rm Moon}}={M_{\rm Sun}\over M_{\rm Moon}}\cdot\left({r_{\rm Moon}\over r_{\rm Earth}}\right)^2\approx170.\)

b) The tidal effect is proportional to the inhomogeneity (derivative) of the gravitational force:

\(\displaystyle F_{\rm tidal}\propto{dF(r)\over dr}\propto{M\over r^3}.\)

So

\(\displaystyle {F_{\rm Sun}^{\rm tidal}\over F_{\rm Moon}^{\rm tidal}}={M_{\rm Sun}\over M_{\rm Moon}}\cdot\left({r_{\rm Moon}\over r_{\rm Earth}}\right)^3\approx0.5.\)

P. 3486. The binding energy of the ¹⁴N nucleus is 16.19 pJ and the ¹⁴C nucleus is 16.37 pJ. Which nucleus is the decay product of the other, and why? (5 points)

The solution will appear at the end of April.

P. 3487. Werner Heisenberg, the Nobel Prize winner German theoretical physicist, was born a hundred years ago (5^th December 1901). With the help of the uncertainty principle introduced by him estimate the uncertainty of the velocity of a carbon atom and an electron `sitting' on the point of a pine needle! (4 points)

Solution. \(\displaystyle Delta\)v_electron\(\displaystyle approx\)1 m/s, v_carbon\(\displaystyle approx\)10^-5 m/s.