Solutions for advanced problems "A" in January, 2002

In this page only the sketch of the solutions are published; in some cases only the final results. To achieve the maximum score in the competition more detailed solutions needed.

A. 281. Given a finite number of points in the plane, no three of which are collinear, prove that it is possible to colour the points with two colours (red and blue) so that every half plane that contains at least three points should contain both a red point and a blue point.

L. Soukup, Budapest

Solution. The following algorithm provides a possible colouring. Consider the convex hull of the points. First colour the vertices of the convex hull red, and colour the interior points blue. Then repeat the following steps while you can: If three consecutive vertices of the convex hull are red and there is no blue point in the triangle formed by the three of them, then change the colour of the middle vertex to blue.

The sequence of steps will always terminate, as the number of points re- coloured is finite. To see that the result is a colouring that satisfies the requirement, it is enough to prove that every half plane that contains exactly three points will necessarily contain both a red point and a blue point.

At least one of any two consecutive vertices of the convex hull is red, as the colouring procedure never produces two consecutive blue vertices.

Now consider a half plane that contains three points. Among these points, there are some consecutive points of the convex hull (it may be a single point), and at most two interior points.

If all three points are red then they are three consecutive vertices of the convex hull, and there are no further points in the triangle they form. This is contradiction, as in that case the colour of the middle point should have been changed to blue.

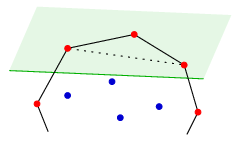
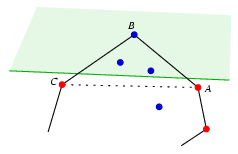
If all three vertices are blue then only one of them can be a point of the convex hull, as the convex hull contains no consecutive blue points. Let that point be B. The neighbouring vertices A and C of the convex hull are then outside the half plane. The point B can only be blue if there are no blue points in the interior of triangle ABC. This is contradiction again, as there are two such blue points known.

A. 282. Are there rational functions f, g and h of rational coefficients such that

(f(x))³+(g(x))³+(h(x))³=x?

Solution. Such functions do exist. Here is one of the most famous examples:

(1)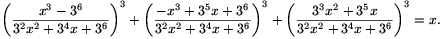

A possible way to find the above identity is as follows. First let us try to find polynomials a(x) and b(x), such that the polynomial a³(x)+b³(x) should have a perfect cube factor of high-enough degree.

Let \(\displaystyle varrho\)=cos120^o+isin120^o be one of the cube roots of unity. In the complex number system, the polynomial a³(x)+b³(x) can be factorized:

(2)	a3(x)+b3(x)=(a(x)+b(x))(a(x)+.b(x))(a(x)+2.b(x)).

The polynomials a(x) and b(x) are chosen to make the two (conjugate) complex factors percfect cubes: a(x)+\(\displaystyle varrho\)^.b(x)=(x-)³ and a(x)+\(\displaystyle varrho\)^2.b(x)=(x-²)³. These are simultaneous linear equations for the polynomials a(x) and b(x), and the solution is

a(x)=x³-3x-1,   b(x)=-3x²-3x.

By completing the perfect cube in the third factor of the right-hand side of (2), we get

a(x)+b(x)=x³-3x²-6x-1=(x-1)³-9x,

and by substituting this and the above into (2):

(x³-3x-1)³+(-3x²-3x)³=(x-)³(x-\(\displaystyle varrho\)²)³((x-1)³-9x)=

=(x²+x+1)^3.((x-1)³-9x).

By division and rearrangement:

\(\displaystyle \bigg({-x^3+3x+1\over x^2+x+1}\bigg)^3+\bigg({3x^2+3x\over x^2+x+1}\bigg)^3+(x-1)^3=9x.\)

Hence the identity (1) is obtained by substituting x/9 for x.

Remark. There are many other solutions possible. As discovered by two of the contestants, another solution is found in The USSR Olympiad Problem Book: Selected Problems and Theorems of Elementary Mathematics by D. O. Shklarsky, N. N. Chentzov, I. M. Yaglom, problem 252).

In the foreword to his book Cubic forms, Yu. I. Manin not only mentions the identity (1), but also proves algebraically that every rational number can be expressed as the sum of the cubes of of three rational numbers. The procedure is a little cumbersome, but it can as well be used for "manufacturing" identities similar to (1).

A. 283. Let n be an integer. Prove that if the equation x²+xy+y²=n has a rational solution, then it also has an integer solution.

Solution 1. We shall prove the following statement: If there exist the real numbers a, b, c, such that c0 and a²+ab+b²=c²n, then the equation x²+xy+y²=n has an integer solution. The statement of the problem follows from this.

If a=b=0, then n=0 and x=y=0 is the only solution. Assume, from now on, that at least one of a and b is not 0. Let us start with the case when a and b are relative primes. Then they are also relatively prime to n. Consider the following identity:

=ab(x²+xy+y²)-c²xy^.n.

It follows from the identity that if either of ax-by or bx-ay is divisible by n, then x²+xy+y² is also divisible by n, as ab and n are relative primes. Now we shall prove the existence of the integers x and y, such that ax-by is divisible by n and x²+xy+y² is small. The principle of the solution is the same as that of problem A. 274. Let H be the set of lattice points (u,v) for which au-bv is divisible by n. These points form a parallelogram lattice, and the area of one lattice parallelogram is equal to the number of possible remainders that a number of the form au-bv may have when divided by n. This area is never more than n. The origin is also an element of the lattice.

It is easy to check that the points of the form u²+uv+v²<2n are the interior points of an ellipse centred at the origin. The area of the ellipse is \(\displaystyle {4\pi\over\sqrt3}n\), which is larger than 4 times the area of a lattice parallelogram. Thus, according to Minkowski's theorem, the ellipse contains another lattice point of H, different from the origin.

Let x,y be a lattice point different from the origin in the interior of the ellipse. By the definition of the lattice points, ax-by is divisible by n, and hence, as seen above, x²+xy+y² is also divisible by n . By the definition of the ellipse, however, 0<x²+xy+y²<2n, and therefore the only possibility is x²+xy+y²=n. Thus the statement is proved for the case when a and b are relative primes.

The case when a and b are not relative primes can be reduced to the case of relative primes. As the equation can be divided by the greatest common factor of a, b and c, we can assume that the greatest common factor of a, b and c is 1. Let d be the greatest common factor of a and b. The number d is relatively prime to c, and d² is a factor of a²+ab+b²=c²n. Hence d² is a factor of n, too. Let A=a/d, B=b/d, C=c and N=n/d². The numbers A és B are relative primes, and A²+AB+B²=C²N. Then it follows from the above that there are integers X and Y, such that X²+XY+Y²=N. From the numbers X and Y, the solution x=X^.d, y=Y^.d is obtained for the ofiginal problem.

(based on several papers)

Solution 2 This is another proof for the statement that if there are real numbers a, b, c, such that c\(\displaystyle ne\)0 and a²+ab+b²=c²n, then the equation x²+xy+y²=n has an integer solution.

The solution uses a few properties of the Euler integers.

Let \(\displaystyle varrho\) be the first complex cube root of unity. Then the number a²+ab+b² is the norm of a+b\(\displaystyle varrho\).

Let p₁^.p₂^....^.p_s be the resolution of a+b\(\displaystyle varrho\) into prime factors in the number system of Euler integers. As the norm is multiplicative, nc²=N(a+b)=N(p₁)^.N(p₂)^....^.N(p_s). The norm of an Euler prime is either a prime number or the square of a prime number. Therefore the factors are of two kinds. In one group of factors the product of the norms is c², and it is n for the rest of them. The product of the Euler primes in the second group is an Euler integer whose norm is n. Thus the Euler integer of the required property exists.