A 2002. januári B-jelű matematika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

B.3512.Keressük meg a 81-nek azt a legkisebb többszörösét,

a) amelyik csak az 1

b) amelyik csak az 1 és a 0 számjegyeket tartalmazza.

Megoldás. Ha egy szám csak az 1 és a 0 számjegyeket tartalmazza és osztható 81-gyel, akkor 9-cel is osztható, és ezért a felírásában szereplő 1-esek száma osztható 9-cel. A legkisebb ilyen szám A=111111111=9^.12345679, és itt B=12345679 9-cel osztva 1 maradékot ad.

Ha egy szám csak az 1 számjegyet tartalmazza és osztható 9-cel, akkor a fentiek értelmében szükségképpen A^.(1+10⁹+10¹⁸+...10^9k) alakú valamilyen k nem negatív egész számmal, ahol a zárójelben szereplő C szám jegyeinek összege k+1. Az AC=9BC szám pontosan akkor osztható 81-gyel, ha BC osztható 9-cel. Mivel B relatív prím a 9-hez, ez pontosan akkor következik be, ha C osztható 9-cel, vagyis ha C jegyeinek összege, k+1 is osztható 9-cel. A legkisebb ilyen számot tehát k=8 választása mellett kapjuk. Az a) feladat megoldása ezek szerint a 81 darab 1-esből álló szám.

Ha egy szám ennél kevesebb számjegyet tartalmaz, akkor legalább 9 darab 1 és legalább 1 darab 0 számjegyet is kell, hogy tartalmazzon, tehát legalább 10-jegyű. Vizsgáljuk meg, van-e megfelelő 10-jegyű szám. Mivel A=9B=9(9k+1)=81k+9, ezért 10A=810k+90, és 10A-9=810k+81 osztható 81-gyel. A b) feladat megoldása tehát az 1111111101 szám.

B.3513. Két körvonal nincs egy síkban, és pontosan két közös pontjuk van. Mutassuk meg, hogy van olyan gömbfelület, amelyre illeszkednek. (3 pont)

Megoldás. Legyen a k₁ kör középpontja O₁, a k₂ köré O₂, és messék egymást az A és B pontokban. Ekkor O₁ és O₂ illeszkedik az AB szakasz felező merőleges síkjára. Ez az F sík merőleges minden olyan síkra, amely az AB szakaszt tartalmazza, így történetesen a k₁ és k₂ körök S₁ illetve S₂ síkjára is. Azon pontok mértani helye, melyektől a k_i kör minden pontja ugyanakkora távolságra van egy, az S_i síkra merőleges, O_i-n áthaladó e_i egyenes. Az e_i egyenes tehát az F síkban helyezkedik el. Mivel S₁ és S₂ nem párhuzamos, az e₁ és e₂ egyenesek sem párhuzamosak. Ennek megfelelően metszik egymást az F sík egy O pontjában. Mármost az O középontú OA sugarú gömb felülete tartalmazza mind a k₁, mind a k₂ kör valamennyi pontját, és ezzel a bizonyítandó állítást beláttuk.

B.3514.Az ABC háromszög magasságai AA₁, BB₁ és CC₁, területe t. Bizonyítsuk be, hogy az ABC háromszög pontosan akkor szabályos, ha

AA₁^.AB+BB₁^.BC+CC₁^.CA=6t.

(3 pont)

Megoldás. Az egyszerűbb írásmód kedvéért vezessük be az AB=c, BC=a, CA=b, AA₁=x, BB₁=y és CC₁=z jelöléseket. Nyilván ax=by=cz=2t. A számtani és mértani közepek közötti egyenlőtlenséget felírva kapjuk, hogy

AA₁^.AB+BB₁^.BC+CC₁^.CA\(\displaystyle ge\)3(xc^.ya^.zb)^1/3=3(ax^.by^.cz)^1/3=6t ,

ahol egyenlőség pontosan akkor áll fenn, ha xc=ya=zb. Ekkor azonban ax=by=cz=2t=xc=ya=zb alapján a=b=c, vagyis a háromszög szükségképpen szabályos. Gondolatmenetünkből az állítás megfordítása is leolvasható minden további nélkül.

B.3515.Bizonyítsuk be, hogy a alakú számok között végtelen sok 2-hatvány van. (4 pont)

Megoldás. Először is, n=1 esetén \(\displaystyle [n\sqrt2]=2^0\). Elegendő megmutatni, hogy ha valamely n természetes számra \(\displaystyle [n\sqrt2]\) 2-hatvány, akkor létezik olyan N>n egész szám is, amelyre \(\displaystyle [N\sqrt2]\) 2-hatvány, hiszen ekkor \(\displaystyle [N\sqrt2]\ge[n\sqrt2]+1\) miatt ez az előzőnél nagyobb 2-hatvány lesz. Tegyük fel tehát, hogy \(\displaystyle [n\sqrt2]\) 2-hatvány, és legyen k olyan egész szám, melyre \(\displaystyle n\sqrt{2}<2^k\). Legyen \(\displaystyle m=[2^k/\sqrt{2}]\), ekkor \(\displaystyle 2^k-\sqrt{2}, akkor \(\displaystyle (m+1)\sqrt{2}<2^k+1\) is fennáll, és így N=m+1 megfelelő lesz. Ha pedig \(\displaystyle \varepsilon\le\sqrt{2}-1\), akkor nyilván \(\displaystyle 2^k-1. Ekkor nyilván \(\displaystyle 2^\ell\varepsilon\le2(\sqrt{2}-1)<1\) is teljesül, és ezért

\(\displaystyle 2^{k+\ell}<(2^{k+\ell}-1)+\sqrt{2}<2^{k+\ell}-2^\ell\varepsilon+\sqrt{2}=(2^lm+1)\sqrt{2}\ .\)

\(\displaystyle (2^lm+1)\sqrt{2}=2^{k+\ell}+\sqrt{2}-2^\ell\varepsilon<2^{k+\ell}+1\ .\)

Mivel \(\displaystyle 2^{k+\ell}-2^\ell\varepsilon+\sqrt{2}=(2^lm+1)\sqrt{2}\), Ebből adódik, hogy most az N=2^m+1 választás megfelelő lesz.

B.3516.A füzetlapra rajzoltunk egy 5 cm-es zárt töröttvonalat. Mutassuk meg, hogy le tudjuk takarni egy 20 Ft-os érmével (az érme átmérője nagyobb, mint 2,5 cm). (3 pont)

Megoldás. Legyen a töröttvonal egyik pontja A és jelölje B a töröttvonalnak azt a pontját ami a töröttvonal mentén (tetszőleges körüljárási irányban) az A ponttól 2,5 cm távolságra van. Jelölje továbbá az AB szakasz felezőpontját O. Azt állítjuk, hogy a töröttvonal bármelyik P pontja O-tól legföljebb 1,25 cm távolságra van. Valóban, legyen P' a P pont O-ra vonatkozó tükörképe, ekkor a PP'A esetleg elfajuló háromszögre a háromszög-egyenlőtlenséget felírva kapjuk, hogy 2|OP|=|PP'|\(\displaystyle le\)|AP|+|AP'|=|AP|+|BP|\(\displaystyle le\)2,5 cm. Ennek megfelelően, ha az érmét úgy helyezzük el, hogy annak középpontja éppen az O pontot fedje, akkor az érme a töröttvonal minden egyes P pontját letakarja.

B.3517.Bizonyítsuk be, hogy 71|61!+1. (4 pont)

Javasolta: Róka Sándor, Nyíregyháza

Megoldás. Mivel a 71 prímszám, Wilson tétele szerint 70!+1 osztható 71-gyel. Elegendő tehát azt megmutatni, hogy 70! ugyanolyan maradékot ad 71-gyel osztva, mint 61!. Vizsgáljuk meg ennek megfelelően az A=62^.63^....^.70 szorzatot.

A\(\displaystyle equiv\)(-9)^.(-8)^....^.(-1)=-72^.7!\(\displaystyle equiv\)-7!=-70^.72\(\displaystyle equiv\)1 (mod 71) ,

vagyis 70!=A^.61!\(\displaystyle equiv\)61! (mod 71), amit bizonyítani akartunk.

B.3518.Igaz-e, hogy ha két tetraéder lapjai megfeleltethetők úgy, hogy az egymásnak megfeleltetett lapok egyenlő területűek, akkor a két tetraéder térfogata is egyenlő? (4 pont)

Megoldás.

Mutatunk egy ellenpéldát. Legyen az egyik tetraéder az egységélű szabályos tetraéder. Ennek térfogata \(\displaystyle \sqrt2/12\). A másik tetraédernek legyen minden lapja egy \(\displaystyle \sqrt3\) magasságú, 1/2 alapú egyenlő szárú háromszög. (Így ennek a lapjai is \(\displaystyle \sqrt3/4\) területűek.)

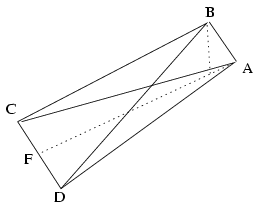
A tetraéder B csúcsához tartozó magassága megegyezik az FAB háromszög B csúcshoz tartozó magasságával, ami az ábra alapján

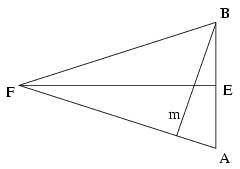
(FA^.m)/2=(AB^.EF)/2

és m²=3-1/16 miatt \(\displaystyle \sqrt{47\over3}\cdot{1\over8}\). Ebből \(\displaystyle V={\sqrt3\over4}\cdot\sqrt{47\over3}\cdot{1\over8}\cdot{1\over3}\neq{\sqrt2\over12}\).

Tehát az állítás nem igaz.

B.3519. Az OA₁A₂A₃ tetraéder OA_i élén lévő, O-tól és A_i-től különböző B_i és C_i pontokra (i=1,2,3) teljesül, hogy az A₁A₂, B₁B₂ és C₁C₂ egyenesek is, és az A₁A₃, B₁B₃ és C₁C₃ egyenesek is egy ponton mennek át. Mutassuk meg, hogy ekkor az A₂A₃, B₂B₃ és C₂C₃ egyenesek egy ponton mennek át vagy párhuzamosak. (4 pont)

Megoldás. Jelölje P, illetve Q az A₁A₂, B₁B₂ és C₁C₂ egyenesek, valamint az A₁A₃, B₁B₃ és C₁C₃ egyenesek metszéspontját. P\(\displaystyle ne\)Q, mert ellenkező esetben P az A₁A₂ és A₁A₃ egyenesek metszéspontja lenne, vagyis P=A₁ lenne, és ekkor szükségképpen B₁ egybeesne A₁-gyel, vagy pedig B₂ egybeesne az O ponttal. Jelölje X\(\displaystyle in\){A,B,C} esetén S_X az X₁, X₂ és X₃ pontok által egyértelműen meghatározott síkot. Mind P, mind Q illeszkedik az S_A, S_B, S_C síkok mindegyikére. E három sík tehát a PQ egyenesben metszi egymást. Ha a P pont illeszkedne az A₂A₃O síkra, akkor illeszkedne az A₂O egyenesre is, vagyis P=A₂ lenne, és ekkor szükségképpen B₂ egybeesne A₂-vel, vagy pedig B₁ egybeesne az O ponttal. Megállapíthatjuk tehát, hogy a PQ egyenes nem illeszkedik az A₂A₃O síkra. Ezért a PQ egyenes vagy elkerüli az A₂A₃O síkot, vagy egy egyértelműen meghatározott R pontban metszi azt.

Ha az A₂A₃, B₂B₃ és C₂C₃ egyenesek mindegyike párhuzamos a PQ egyenessel, akkor egymással is párhuzamosak. Ha valamelyik egyenes, mondjuk X₂X₃, nem párhuzamos PQ-val, akkor szükségképpen metszi PQ-t, hiszen X₂X₃ és PQ is az S_X síkban van. Mivel X₂X₃ az A₂A₃O síkban helyezkedik el, ez a metszéspont megegyezik az R ponttal. Ha az A₂A₃, B₂B₃ és C₂C₃ nem párhuzamosak egymással, akkor valamely Y\(\displaystyle in\){A,B,C}\{X} esetén az A₂A₃O síkban lévő, egymással nem párhuzamos X₂X₃ és Y₂Y₃ egyenesek egy T pontban metszik egymást. Ez a T pont illeszkedik az S_X és S_Y síkokra. E két sík nem eshet egybe, ellenkező esetben ugyanis X₂X₃ és Y₂Y₃ is egybeesnének. Ennélfogva T illeszkedik a PQ egyenesre is. Másrészt T az X₂X₃ és Y₂Y₃ egyeneseket tartalmazó A₂A₃O síkra is illeszkedik, vagyis T=R. Ha {A,B,C}\{X,Y}={Z}, akor az Z₂Z₃ egyenes metszi vagy az X₂X₃, vagy az Y₂Y₃ egyenest, és e két egyenes U metszéspontjára az előzőhöz hasonló módon igaz, hogy U=R. Összefoglalva megállapíthatjuk, hogy ha a három egyenes nem párhuzamos egymással, akkor szükségképpen a PQ egyenes metszi az A₂A₃O síkot egy R pontban, és a három szóban forgó egyenes R-ben metszi gyemást.

B.3520. A valós számok közül bizonyosakat pirosra festünk, mégpedig úgy, hogy ha az x szám piros, akkor az x+1 és \(\displaystyle {x\over x+1}\) számokat is pirosra festjük. Mely számok lesznek pirosak, ha kezdetben csak az 1 piros? (5 pont)

Megoldás. Ha x pozitív racionális szám, akkor x+1 és \(\displaystyle {x\over x+1}\) is az, ezért csakis pozitív racionális számokat festhetünk pirosra. Megmutatjuk, hogy minden egyes pozitív racionális szám előbb-utóbb piros lesz. Ez nyilván igaz az 1 nevezőjű törtekre, hiszen ezek az 1 számból az 1 ismételt hozzáadásával előállíthatók. Tegyük fel, hogy valamely n pozitív egész esetén már igazoltuk, hogy minden egyes legfeljebb n nevezőjű pozitív törtszám előbb-utóbb piros lesz. Tekintsük ezek után bármelyik n+1 nevezőjű 1-nél kisebb pozitív törtet, legyen ez \(\displaystyle {m\over n+1}\), ahol m\(\displaystyle le\)n. Az \(\displaystyle {x\over x+1}={m\over n+1}\) egyenlet megoldása, \(\displaystyle x={m\over n+1-m}\) n-nél nem nagyobb nevezőjű pozitív tört, ez tehát valamikor piros lesz, és a következő lépésben már \(\displaystyle {m\over n+1}\) is az lesz. Mivel az egész számok kivételével minden egyes n+1 nevezőjű pozitív tört az 1 ismételt hozzáadásával valamely \(\displaystyle {m\over n+1}\) alakúból (1\(\displaystyle le\)m\(\displaystyle le\)n) előállítható, előbb-utóbb az is piros lesz. A teljes indukció elve miatt tehát minden pozitív racionális szám piros lesz.

B.3521. Egy baktériumtörzs minden tagja egy óra leteltével vagy elpusztul vagy pedig kettéosztódik. Ha az osztódás valószínűsége p, akkor mennyi a valószinűsége annak, hogy egy kiszemelt baktérium leszármazottai sosem halnak ki? (5 pont)

Megoldás. Jelöljön A egy kiszemelt baktériumot, és feltéve, hogy kettéosztódik, a közvetlen leszármazottjait jelölje B és C. Legyen x annak a valószínűsége, hogy A leszármazottai sosem halnak ki. Feltéve, hogy B és C létrejött, jelölje y annak a valószínűségét, hogy vagy B, vagy C leszármazottai nem halnak ki; ekkor x=py. Ha már B és C létrejött, akkor annak a valószínűsége, hogy B leszármazottai nem halnak ki, x-szel egyenlő, és ugyanennyi annak a valószínűsége is, hogy C leszármazottai nem halnak ki. Annak a valószínűsége pedig, hogy sem B sem C leszármazottai nem halnak ki, ezen események függetlenségét feltételezve, x²-tel egyenlő. Ezért y=x+x-x², x=p(2x-x²), ahonnan leolvasható, hogy x értéke vagy 0, vagy 2-1/p. Mivel 0\(\displaystyle le\)x\(\displaystyle le\)1, ezért p\(\displaystyle le\)1/2 esetén szükségképpen x=0, p>1/2 esetén pedig x=2-1/p.