Solutions for exercises "C" in January, 2002

In this page only the sketch of the solutions are published; in some cases only the final results. To achieve the maximum score in the competition more detailed solutions needed.

C.655. Whenever there is a lottery draw, Barnie's grandmother sets aside some change in a piggy bank for her grandson. Grandma is a lady of firm discipline; she always observes the following rules:

1) She only puts coins in the piggy bank.

2) When a number is drawn, she immediately places that number of forints (HUF) in the piggy, using the lowest possible number of coins.

3) When the lottery draw is over, she counts how many of each kind of coin she has put in the piggy.

One day, when 7 numbers were drawn out of the first 35 positive integers, she counted 3 20-forint coins, 6 10-forint coins, 5 5-forint coins, 9 2-forint coins, and 3 1-forint coins. What were the 7 numbers drawn?

Note: There exist the following coins in Hungarian currency: 100, 50, 20, 10, 5, 2, and 1-forint (HUF) coins.

Solution. By considering all cases and some thinking, the following solution is obtained:

1st number: 20+10+2+2=34

2nd number: 20+10+2+1=33

3rd number: 20+5+2+2=29

4th number: 10+5+2+2=19

5th number: 10+5+2+1=18

6th number: 10+5+2=17

7th number: 10+5+1=16

C.656. A jacket with an original price of 21,250 forints (HUF) was put on sale. Then, with the start of the great Christmas sale, its price was reduced again, this time to 19,176 forints. By what percentage was the price reduced each time, given that both percentages of reduction were one-digit numbers?

Solution.

Let one price reduction be a%, and the other b%. Then 0,9a^.09b=0,9024, or what is equivalent, (90+a)(90+b)=9024.Hence 924=90(a+b)+ab. It immediately follows that ab ends in 4. On the other hand, since ab\(\displaystyle le\)81, it follows that 90(a+b)\(\displaystyle ge\)843=90^.9,3666, and thus a+b\(\displaystyle ge\)10. Similarly, it follows from 924\(\displaystyle ge\)90(a+b) that a+b\(\displaystyle le\)10. Therefore a+b=10, and ab ends in 4, which implies that either a=4 and b=6 or the other way round, a=6 and b=4. Thus one reduction was by 4 percent, and the other by 6 percent.

C.657. A cone and a cylinder have equal heights and equal volumes. Find the apex angle of the cone if the areas of the lateral surfaces are also equal!

Solution. The cone is clearly a right circular cone. Let m denote the common height of the cone and the cylinder, let r and R be the radii of the bases of the cone and cylinder, respectively, let a denote the slant height of the cone and let 2\(\displaystyle alpha\) be its apex angle.

Since the volumes are equal, \(\displaystyle {{r^2\pi m}\over3}=R^2\pi m\), and hence \(\displaystyle r/R=\sqrt3\). Since the lateral surfaces are also equal \(\displaystyle pi\)ra=2R\(\displaystyle pi\)m, it follows that cos\(\displaystyle alpha\)=m/a=r/2R. With the result above, that means \(\displaystyle {{\sqrt3}\over2}=\cos30^{\circ}\). Hence 2\(\displaystyle alpha\)=60^o. The apex angle of the cone is 60^o.

C.658. Solve the simultaneous equations

\(\displaystyle {1\over x}+{1\over y}={1\over z};\quad{1\over x+15}+{1\over y-6}={1\over z};\quad{1\over x+24}+{1\over y-15}={1\over z}\)

Solution. Since the right-hand side of each equation is 1/z, the left-hand sides are equal. With a little rearrangement, that means \(\displaystyle {{xy}\over{x+y}}={{(x+24)(y-15)}\over{x+y+9}}={{(x+15)(y-6)}\over{x+y+9}}.\) By multiplying on both sides of the first equation and some more calculation y=x+30 is obtained. Substitution into the second equation and a similar rearrangement leads to the quadratic equation x²+80x+1200=0. Hence x₁=-20, x₂=-60, and thus y₁=10, y₂=-30. Finally, it follows from the original first equation that z₁=20, z₂=-20. It can be checked by substitution that these values satisfy the equations..

C.659. For what values of the real parameter 0\(\displaystyle le\)t does the equation sin (x+t)=1-sinx have no solution?

Solution. By rearranging the equation, we get sin(x+t)+sinx=1, and hence 2sin(x+t/2)^.cos(t/2)=1. If cos(t/2)=0, the equation has no solution. Otherwise we can divide by 2cos(t/2) (which only depends on t, and thus can be considered a parameter) to obtain sin(x+t/2)=1/(2cos(t/2)). the equation has a solution if and only if the right-hand side falls between -1and 1, that is, -1\(\displaystyle le\)1/(2cos(t/2))\(\displaystyle le\)1, which means -2\(\displaystyle le\)1/(cos(t/2))\(\displaystyle le\)2. 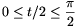Since 0\(\displaystyle le\)t\(\displaystyle le\), it follows that , and thus cos(t/2)0. Therefore the inequality on the left-hand side will always be true. The inequality on the right-hand side will be true if and only if cos(t/2)1/2. In that case, the equation has a solution. It has no solution (including the case of cos(t/2)=0), if 0cos(t/2)<1/2, that is, 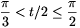. The equation has no solution if