A 2002. januári informatika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

I. 13. Egész számokat a 10-es mellett -10-es számrendszerben is felírhatunk, a következőképpen:

x=x₀+(-10)^.x₁+(-10)²^.x₂+...+(-10)ⁿ^.x_n

ahol 0$\displaystyle le$x_i$\displaystyle le$9. Ebben a számrendszerben minden egész szám felírható előjelnélküli egész számként. Készítsünk programot (I13.pas, I13.c, ...), amely egy legfeljebb négyjegyű 10-es számrendszerbeli számot -10-es számrendszerbelivé vált, illetve fordítva: -10-esből 10-esbe?

Példák:

10-es	(-10)-es számrendszer
`3`	`3`
`-6`	`14`	(=-10+4)
`34`	`174`	(=100-70+4)
`-72`	`88`	(=-80+8)
`163`	`243`	(=200-40+3)
`-527`	`1533`	(=-1000+500-30+3)
`1526`	`19686`	(=10000-9000+600-80+6)
`1994`	`18014`	(=10000-8000+0-10+4)

(10 pont)

Forrásértelmezés:

Program JAN1;
    Konstans
      MaxN=100;
    Típus

Itt tároljuk a számot, olyan formátumban, hogy tároljuk a hosszát, vagyis a számjegyek számát, illetve a számjegyeket.

      Szám = Rekord( db : Egész; jegy : Tömb(0..MaxN:Egész))

Kiíratjuk, hogy milyen lehetőségek közül lehet választani.

    Ki: Menü(Számrendszer konverzió,		
  1. Tízesből mínusz tízesbe,			
  2. Mínusz tízesből tízesbe)

Beolvassuk a választott menüpont számát, majd annak megfelelően elágazunk és elvégezzük a tízesből mínusztízesbe vagy a második pont választása esetén a mínusztízesből tízes számrendszerbe történő átváltást.

    Be: c						
    Ha c='1'					
      akkor tizminusz				
      különben Ha c='2'				
        akkor minusztiz;			
  Program vége.

  Eljárás tizminusz;
    Változók
      tizes, mtizes : Szám;
      i, j: Egész;
    Ki: A szám tízes számrendszerben?

Beolvassuk a tízes számrendszerben levő számot.

    beolvas(tizes);

A mínusztízes számrendszerben levő számnak legalább annyi lesz a számjegyei száma, mint a tízes számrendszerben levőnek.

    mtizes.db:=tizes.db;				
    Ciklus i:=0-tól MaxN-ig

Kinullázzuk a számjegyeket.

      mtizes.jegy[i]:=0;				
    Ciklus vége;
    Ciklus i:=mtizes.db-tól 0-ig -1-esével

A jegyek indexe az jelenti, hogy a számjegy, melyik helyiértékhez tartozik, vagyis az alap hányadik hatványát kell a számjeggyel megszorozni. Ezért a balról jobbra való feldolgozásnál a páros indexű helyen levő számjegy megegyezik a tízes és mínusz tízes számrendszerben. Viszont a páratlan index esetén komolyabb feldolgozásra van szükség. Paraméterként kapjuk meg a mínusz tízes számrendszerben felírt számot, átadjuk az indexet és a tízes számrendszerben felírt szám aktuális számjegyét.

        Ha i mod 2=0				
          akkor    mtizes.jegy[i]:=tizes.jegy[i]
          különben negativ(mtizes,i,tizes.jegy[i]);
        Elágazás vége
    Ciklus vége;

Végül kiíratjuk a számot.

    Ki: A szám mínusztízes számrendszerben:	
    kiir(mtizes);
  Eljárás vége

  Eljárás negativ(sz: Szám; i, mit: Egész;);

Ha a számjegy 0, akkor a mínusz tízes számrendszerben felír számjegy is az.

    Ha mit=0					
      akkor    sz.jegy[i]:=0			
      különben Ciklus

Különben a mínusz tízes számrend-szerben úgy tudjuk felírni a jegyet,hogy ezen a helyi értékű helyen szereplő számot kivonjuk tízből és az eggyel nagyobb helyen szereplő számjegyet növeljük eggyel.

                 sz.jegy[i]:=10-mit;		
                 i:=i+1;				
                 sz.jegy[i]:=sz.jegy[i]+1;

Ha ez tíz, akkor már nem tudjuk egy jeggyel leírni, ezért ez nulla lesz, az azutáni pedig eggyel kisebb, hiszen mínusz tízes számrend-szerbe írjuk fel a számot.

                 Ha sz.jegy[i]=10			
                   Akkor sz.jegy[i]:=0;	
                         i:=i+1;			
                         sz.jegy[i]:=sz.jegy[i]-1	

                 Elágazás vége;

Ha nullánál kisebb a következő számjegy, akkor úgy ismételjük ezta részt, mintha egyet kellene átírnunk ezen a helyiértéken.

                 Ha sz.jegy[i]<0			
                   akkor mit:=1;
                 Elágazás vége;

Ezt kell ismételnünk, amíg nullánál kisebb a következő számjegy.

               amíg sz.jegy[i]<0			
               Ciklus vége;

Ha közben nőtt a számjegyek száma, akkor azt elmentjük.

               Ha i>sz.db				
                 Akkor sz.db:=i;			
               Elágazás vége;
    Elágazás vége;
  Eljárás vége;

  Eljárás minusztiz;
    Változók
      tizes, mtizes: Szám;
      i,j: Egész;
    Ki: A szám mínusztízes számrendszerben?

Beolvassuk a mínusz tízes számrendszerben felírt számot, amit feldolgozunk.

   beolvas(mtizes);

A tízes számrendszerben felírt szám számjegyeinek száma kezdetben nulla.

     tizes.db:=0;

Kinullázzuk a számjegyeket.

    Ciklus i:= 0-tól MaxN-ig
      tizes.jegy[i]:=0;				
    Ciklus vége

Az összes számjegyet fel kell dolgoznunk. A legnagyobb helyi értékűtől a legkisebbig.

    Ciklus i:=mtizes.db-től 0-ig -1-esével

A páros és páratlan indexű helyen álló számjegyeket máshogy kell feldolgozni.

      Ha i mod 2=0				
        akkor    hozzaad(tizes,i,mtizes.jegy[i])	
        különben levon(tizes,i,mtizes.jegy[i]);	
      Elágazás vége;
    Ciklus vége;
    Ki: A szám tízes számrendszerben:;

Végül kiíratjuk a tízes számrendszerben felírt számot.

    kiir(tizes);					
  Eljárás vége;

  Eljárás hozzaad(sz: Szám; i, mit: Egész);
    Változók

Ha az egyesek, százasok és így tovább a mínusz tíz páros hatványon szereplő helyi értékű jegyét vesszük, akkor ezzel a számjeggyel növelnünk kell a már ott szereplő számot. Van ott szám. Legalább a nulla, de előfordulhat, hogy a feldolgozás során már kapott értéket ez a jegy.

      j: Egész;

Tehát hozzáadjuk.

    sz.jegy[i]:=sz.jegy[i]+mit;

Majd megvizsgáljuk a számjegyeket, hiszen csak egyjegyű szerepelhet számjegyként. Ezért a kilencnél nagyobb számokbólkivonunk 9-et, majd a következő, egyel magasabb helyi értéken szereplő jegyhez hozzáadunk egyet. És megismételjük az ellenőrzést.

    Ciklus amíg sz.jegy[i]>9			
       sz.jegy[i]:=sz.jegy[i]-10;			
      i:=i+1;					
      sz.jegy[i]:=sz.jegy[i]+1;		
    Ciklus vége;

Végül ha nőtt az értékes számjegyek száma, akkor azt elmentjük.

    Ha i>sz.db					
      akkor sz.db:=i;				
    Elágazás vége;
  Eljárás vége;

  Eljárás levon(sz: Szám; i, mit: Egész);
    Változók

Másik esetben - amikor a mínusz tízesek, mínusz ezresek, stb -, vagyis amikor páratlan indexű jegyekkel foglalkozunk.

      j: Egész;

Csökkentjük az aktuális számjegy értékét.

    sz.jegy[i]:=sz.jegy[i]-mit;

Majd itt is ellenőrzést hajtunk végre, hiszen a számjegy nem lehet negatív. Vagyis hozzá kell adnunk tízet. A következő jegyet pedig eggyel csökkentjük.

    Ciklus amíg sz.jegy[i]<0			
       sz.jegy[i]:=sz.jegy[i]+10;			
      i:=i+1;				
      sz.jegy[i]:=sz.jegy[i]-1;			
    Ciklus vége;
  Eljárás vége;

  Eljárás beolvas(sz: Szám);
    Változók
      s: szöveg;
      i,j: Egész;

Beolvasunk egy számokból álló szöveget, melynek összes karakterét feldolgozzuk, vagyis mindegyik karaktert egy-egy számjegyé alakítunk. A legutolsó karakter lesz a számjegyek között a nulla indexű, hiszen ez felel meg az egyeseknek (10 a nulladikon).

    Be: s;					
    sz.db:=Hossz(s)-1;				
    Ciklus i:=0-től sz.db-ig			
      val(s[sz.db-i+1],sz.jegy[i],j);		
					
						
    Ciklus vége;
  Eljárás vége;

  Eljárás kiir(sz: Szám);
    Változók
      i,j: Egész;

Fordított sorrendben íratjuk ki a számjegyeket, de csak azokat, melyek nem nullák.

    i:=sz.db;					
    Ciklus amíg (i>0) ÉS (sz.jegy[i]=0)		
      i:=i-1;
    Ciklus vége;

Az összes többi kiíratásra kerül.

    Ciklus j:=i-től 0-ig -1-esével		
      Ki: sz.jegy[j];
    Ciklus vége;
  Eljárás vége;

Pascal program:

Program negativ;

  uses newdelay,crt;
  const maxn=100;
  type szam=record
              db: integer;
              jegy: array [0..maxn] of integer;
            end;
  var c: char;

  Procedure beolvas(var sz: szam);
    var s: string;
        i,j: integer;
  begin
    readln(s);
    sz.db:=length(s)-1;
    for i:=0 to sz.db do val(s[sz.db-i+1],sz.jegy[i],j);
  end;

  Procedure kiir(sz: szam);
    var i,j: integer;
  begin
    i:=sz.db; while (i>0) and (sz.jegy[i]=0) do i:=i-1;
    for j:=i downto 0 do write(sz.jegy[j]);
    writeln;
  end;

  Procedure tizminusz;
    var tizes,mtizes: szam;
        i,j: integer;
    Procedure negativ(var sz:szam; i: integer; mit: integer);
    begin
      if mit=0 then sz.jegy[i]:=0 else
      begin
        repeat
          sz.jegy[i]:=10-mit; i:=i+1; sz.jegy[i]:=sz.jegy[i]+1;
          if sz.jegy[i]=10 then
          begin
            sz.jegy[i]:=0; i:=i+1; sz.jegy[i]:=sz.jegy[i]-1
          end;
          if sz.jegy[i]<0 then mit:=1;
        until sz.jegy[i]>=0;
        if i>sz.db then sz.db:=i;
      end
    end;
  begin
    write('A szám tizes számrendszerben?');
    beolvas(tizes); mtizes.db:=tizes.db;
    for i:= 0 to maxn do mtizes.jegy[i]:=0;
    for i:=mtizes.db downto 0 do
      if i mod 2=0 then mtizes.jegy[i]:=tizes.jegy[i]
                   else negativ(mtizes,i,tizes.jegy[i]);
    write('A szám minusz tizes számrendszerben:');
    kiir(mtizes)
  end;

  Procedure minusztiz;
    var tizes,mtizes: szam;
        i,j: integer;

    Procedure hozzaad(var sz: szam; i: integer; mit: byte);
      var j: integer;
    begin
      sz.jegy[i]:=sz.jegy[i]+mit;
      while sz.jegy[i]>9 do
      begin
        sz.jegy[i]:=sz.jegy[i]-10; i:=i+1; sz.jegy[i]:=sz.jegy[i]+1;
      end;
      if i>sz.db then sz.db:=i;
    end;

    Procedure levon(var sz: szam; i: integer; mit: byte);
      var j: integer;
    begin
      sz.jegy[i]:=sz.jegy[i]-mit;
      while sz.jegy[i]<0 do
      begin
        sz.jegy[i]:=sz.jegy[i]+10; i:=i+1; sz.jegy[i]:=sz.jegy[i]-1;
      end;
    end;

  begin
    write('A szám minusz tizes számrendszerben?');
    beolvas(mtizes); tizes.db:=0;
    for i:= 0 to maxn do tizes.jegy[i]:=0;
    for i:=mtizes.db downto 0 do
      if i mod 2=0 then hozzaad(tizes,i,mtizes.jegy[i])
                   else levon(tizes,i,mtizes.jegy[i]);
    write('A szám tizes számrendszerben:');
    kiir(tizes);
  end;

begin
  clrscr; writeln('                Számrendszer konverzió'); writeln;
  writeln('1. Tizesből minusz tizesbe');
  writeln('2. Minusz tizesből tizesbe');
  writeln; write('Melyiket kéred?'); readln(c);
  if c='1' then tizminusz else if c='2' then minusztiz;
  readkey;
end.

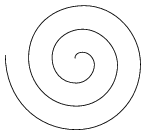
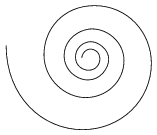
I. 14. Az arkhimédeszi spirális jellemzője, hogy a körbetekeredő spirál pontjai az előző körbelitől mindig azonos távolságra vannak. A logaritmikus spirális esetén pedig ezek a távolságok körbe-fordulásonként egy konstanssal szorzódnak.

Készítsünk programot (I14.pas, I14.c, ...), amely beolvassa a körbefordulások számát, majd ilyen arkhimédeszi és logaritmikus spirálist rajzol a képernyőre?


Arkhimédeszi spirál	Logaritmikus spirál

(10 pont)

Forrásértelmezés:

Program JAN2;
    Változók
      a, k, r, f, N: Valós;
      x, y, xa, ya, xl, yl: Egész;

    Eljárás Arkhimedeszi(r, f: Valós);

Az Arkhimédeszi spirál képlete: r=a^.$\displaystyle varphi$. Az f fokban szerepel, ezért radiánba számoljuk át.

      r:=a*pi*f/180;				
  
    Eljárás vége;

    Eljárás Logaritmikus(r, f: Valós);

A Logaritmikus spirál képlete: 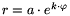$r=a\cdot e^{k\cdot\varphi}$ . f itt is fok, amit ugyancsak átszámítunk radiánba. k értékét számítjuk, míg a konstans 10.

      r:=10*exp(k*pi*f/180);			
  
    Eljárás vége;

    Eljárás Polar2Descartes(r, f: Valós; x, y: Egész);

A polárkoordinátákkal megadott pont távolság és szög értékeiből kiszámítjuk a derékszögű koordinátarendszerben levő x és y koordinátákat.

      x:=Kerekít(r*cos(pi*f/180));

Ez egyszerű a szögfüggvényekkel. Egész értékekre kerekítünk, hiszen csak egész koordinátákat tudunk kirajzolni.

      y:=Kerekít(r*sin(pi*f/180));		
						
    Eljárás vége;

Beolvassuk a körbefordulások számát.

    Be: N;					
    Grafikus_felület_beállítása;

Feketével fogunk rajzolni.

    SzínBeállítás(FEKETE);

Választó vonal a két spirális között a 640x320-as rajzlapon.

    Vonal(320,0,320,320);

Az Arkhimédeszi spirálhoz ki kell számítanunk az egyes fordulatoknál levő konstans értékét. Ennyivel kell szorozni a szöget.

    a:=150/N/2/pi;

A Logaritmikus spirál kitevőjében szereplő konstans kiszámítása, hogy kiférjen a képernyőre az ábra.

    k:=ln(15)/N/2/pi;

Nulla szögnél kezdünk.

    f:=0;

Kezdetben a középpontban állunk.

    xa:=160;

Kezdetben a középpontban állunk.

    ya:=160;

Kezdetben a középpontban állunk.

    xl:=480;

Kezdetben a középpontban állunk.

    yl:=160;					
    Ciklus amíg f<N*360

Kiszámítjuk az ehhez a szöghöz tartozó sugarat az Arkhimédeszi spirális esetén.

      Arkhimedeszi(r,f);

Kiszámítjuk a polárkoordinátákhoz tartozó Descartes koordinátákat.

      Polar2Descartes(r,f,x,y);

Eltoljuk a megfelelő középpontba a spirálist.

      x:=160-x;					
      y:=160-y;

Vonalat rajzolunk az előző és az új pont között.

      Vonal(xa,ya,x,y);

Lementjük az Arkhimédeszi spirális új pontjának koordinátái.

      xa:=x;					
      ya:=y;

Kiszámítjuk az ehhez a szöghöz tartozó sugarat a Logaritmikus spirális esetén.

      Logaritmikus(r,f);

Kiszámítjuk a polárkoordinátákhoz tartozó Descartes koordinátákat.

      Polar2Descartes(r,f,x,y);

Eltoljuk a megfelelő középpontba a spirálist.

      x:=480-x;					
      y:=160-y;

A legelsőt nem, de a többi vonalat kirajzoljuk az előző pont és az új pont között.

      Ha f<>0					
       akkor Vonal(xl,yl,x,y);			
      Elágazás vége;

Lementjük a Logaritmikus spirális új pontjának koordinátáit is.

      xl:=x;					
      yl:=y;

A szög növelése.

      f:=f+1;					
    Ciklus vége;
    Grafikus_felület_bezárása;
  Program vége.

I. 15. Egy állatpopuláció tagjai maximum 10 évig élnek, a 10 korosztály létszámát tároljuk. Minden egyes korosztályhoz megadjuk, hogy egy egyede milyen eséllyel hal meg egy-egy évben (halálozási ráta), illetve átlagosan hány utódja születik (születési ráta).

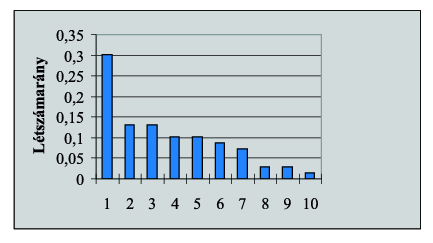
Készítsünk táblázatot (I15.xls), amely tartalmazza a születési és halálozási rátákat, a kezdő létszámot, majd billentyű (billentyűkombináció) lenyomására számolja a következő évbeli korosztály-létszámokat és diagramot rajzol az egyes korosztályok összpopuláción belüli arányáról? Egy másik billentyű (billentyűkombináció) hatására pedig álljon vissza újra az 1. időpontba, a kezdőlétszámmal? Ha a létszámok számolásakor valós számok jönnének ki, azokat egészre kell kerekíteni?

Példa: (az 1. időegységben minden korosztályban 1000 állat volt)

Születési ráta:	Halálozási ráta:	Idő:	2
0,1	0,1	1. korcsoport:	2080
0,1	0,1	2. korcsoport:	900
0,4	0,3	3. korcsoport:	900
1,1	0,3	4. korcsoport:	700
0,9	0,4	5. korcsoport:	700
0,4	0,5	6. korcsoport:	600
0,3	0,8	7. korcsoport:	500
0,2	0,8	8. korcsoport:	200
0,1	0,9	9. korcsoport:	200
0	1	10. korcsoport:	100
		Létszám:	6880

(10 pont)

Megoldás:

A kezdeti állapotot legegyszerűbben úgy állíthatjuk vissza, ha egy különálló területen lementjük az adatokat, és a megfelelő billentyűkombinációra visszamásoljuk a kezdeti értékeket. Ezt legegyszerűbben egy Visual Basic makróval tehetjük meg.

  Sub Ujra()

Erre a területre mentettük a kezdeti értékeket, amit most ki kell jelölnünk.

      Range("D21:D32").Select

A vágólapra kell másolnunk.

      Selection.Copy

Majd a helyére, jelen esetben a D6-os cellától kezdődően be kell másolni a Munkalapra.

      Range("D6").Select				
      ActiveSheet.Paste				
  End Sub

A következő időpont állapotát pedig ugyancsak kiszámolhatjuk egy másik területre, például a mellette levő oszlopba, amit ismét csak át kell másolnunk, ha leütünk egy másik billentyűkombinációt. A Visual Basic makró itt is egyszerű:

  Sub MASOL()

Ezen a területen található következő időpont korcsoportjainak egyedszámai, amit kijelölünk, vágólapra másolunk, majd a helyére, a szomszédos oszlopba, ugyanekkora területre másoljuk irányított beillesztéssel úgy, hogy csak az értékeket másoljuk, nem végzünk semmilyen műveletet, nem ugorjuk át az üreseket és nincs transzponálás.

      Range("E6:E17").Select			
      Selection.Copy				
      Range("D6:D17").Select			
      Selection.PasteSpecial _			
      Paste:=xlValues, _				
      Operation:=xlNone, _			
      SkipBlanks:=False, _			
      Transpose:=False				
  End Sub

Ezeket a makrókat meg is írhatjuk, de az Eszközök/Makró >/Új makró rögzítése... menüpont választásával ki is menthetjük.

[E7] =SZORZATÖSSZEG(E8:E16;$A7:$A15) a következő időpontban az első korcsoportba tartozó egyedek száma függ az összes többi korcsoporttól, hiszen bárhonnan születhet új egyed. Így itt egy összeget kell képeznünk. Mégpedig a megfelelő egyedszámot kell a születési rátával megszoroznunk és azok összegét vennünk. Persze csak az életben maradottaknak lehet utóduk.

[E10] =D9*(1-$B$9) a következő időpontban ezen korosztály egyedeinek a száma, hiszen a az előző időpontban levő egyedek közül annyi marad életben, amennyit az összes mínusz a halálozási rátával számolt egyedszámból tudunk megadni. Persze eltolás van közben, hiszen a következő időpontban ez a korcsoport már a következő lesz.

[E17] =SZUM(E7:E16) Az összes egyed száma nagyon egyszerű, hiszen ez az összegük.

A megoldás letölthető innen.

Már regisztráltál?
Új vendég vagy?