Solutions for problems "B" in February, 2002

In this page only the sketch of the solutions are published; in some cases only the final results. To achieve the maximum score in the competition more detailed solutions needed.

B.3522.Solve the following equation on the set of integers: 2x⁴+x²y²+5y²=y⁴+10x². (3 points)

Solution. If A=x² and B=y², then by rearranging the equation and factoring we get (2A-B)(A+B-5)=0. Thus either 2x²=y², and hence x=y=0, or x²+y²=5. Therefore, the equation has the following 9 solutions: x=y=0, x=$\displaystyle pm$2,y=$\displaystyle pm$1, valamint x=$\displaystyle pm$1,y=$\displaystyle pm$2.

B.3523.Given a semicircle, consider the triangles in which the diameter of the semicircle is contained in one side, and the other two sides are tangent to the semicircle. Which of these triangles has minimum area? (4 points)

Solution. If the triangle is reflected in the line containing the diameter, the sides of the resulting kite will all touch the given circle. We shall prove that out of all such kites, the square has minimum area. Then it follows that the triangle of minimum area is the isosceles right triangle whose hypotenuse contains the diameter of the semicircle. Let us prove a more general statement: Out of all quadrilaterals circumscribed around a given circle, the square has the minimum area. Let the radius of the circle be unity. Consider a quadrilateral whose sides touch the circle and whose angles are $\displaystyle pi$-2$\displaystyle alpha$,$\displaystyle pi$-2$\displaystyle beta$,$\displaystyle pi$-2$\displaystyle gamma$,$\displaystyle pi$-2$\displaystyle delta$, where the sum of the acute angles $\displaystyle alpha$,$\displaystyle beta$,$\displaystyle gamma$,$\displaystyle delta$ is $\displaystyle pi$. Then the area of the quadrilateral is

$\displaystyle \tan\alpha+\tan\beta+\tan\gamma+\tan\delta\le4\tan\Bigl({\alpha+\beta+\gamma+\delta\over4}\Bigr)=4\tan(\pi/4)=4\ ,$

as the tangent function is strictly convex down on the interval (0,$\displaystyle pi$/2). For the same reason, equality only occurs in the case $\displaystyle alpha$=$\displaystyle beta$=$\displaystyle gamma$=$\displaystyle delta$=$\displaystyle pi$/4, that is, when all angles of the quadrilateral are right angles. That completes the proof.

B.3524.The sum of the real numbers x and y is 1. Find the maximum value of xy⁴+x⁴y. (3 points)

Solution. As

xy⁴+x⁴y=xy(x³+y³)=xy((x+y)³-3xy(x+y))=xy(1-3xy) ,

the task is to find the maximum of the expression A(1-3A), given that the number A can be written in the form x(1-x). As

$\displaystyle A(1-3A)={1\over12}-3\Bigl(A-{1\over6}\Bigr)^2\ ,$

the the expression A(1-3A) assumes its maximum at the point A=1/6, and the value of the maximum is 1/12. It follows from the solution of the quadratic equation x(1-x)=1/6 that if $\displaystyle x=(1\pm\sqrt{1/3})/2$, then A=1/6=x(1-x). Thus the maximum of the expression A(1-3A) on the given condition will also be 1/12.

B.3525.Prove that there are infinitely many composite numbers in the sequence 1,31,331,3331,... . (4 points)

Solution. 31 is a prime number. It follows from Fermat's little theorem that 31 is a factor of the number 10³⁰-1, and therefore it is also a factor of any number of the form 10^30k-1, where k is a positive integer. Thus it is also a factor of one third of such a number, that is, any number that consists of 30k digits of 3. By multiplying such a number by 100 and adding 31, the result is also divisible by 31, and all numbers obtained in this way belong to te sequence. Therefore, from 31 onwards, every 30th member of the sequence is a composite number, as it is divisible by 31.

B.3526. F is the midpoint of side BC of a rectangle ABCD, and H divides side CD in the ratio 1:2, CH being the shorter part. How large may the angle HAF be? (4 points)

Solution.

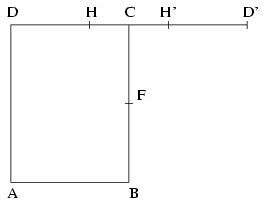
Let the points D and C be fixed, and let D' and H' denote the reflections of D and H about the point C, respectively. Suppose that the angle HAF has a given measure $\displaystyle gamma$. Where can the point A be then? The point A pont lies on the perpendicular drawn to DC at D, and it also lies on a circular arc connecting H and D' and centred on the perpendicular line drawn to CD atH'. The arc is the locus of the points where HD' subtends an angle $\displaystyle gamma$. Thus the radius of the circle is at least DH'=HD', and in that case the central angle subtended by the segment HD' is $\displaystyle pi$/3, $\displaystyle gamma$=$\displaystyle pi$/6. If the radius of the circle is increased, the value of $\displaystyle gamma$ will decrease monotonically to 0, and the point A can be constructed in each case. Therefore, the measure of the angle HAF can be any positive number not greater than $\displaystyle pi$/6.

B.3527. Given a trapezium in which the other two sides are not parallel, construct, using a straight edge only, a line whose segment between the non-parallel sides is divided into three equal parts by the diagonals of the trapezium. (5 points)

Solution.

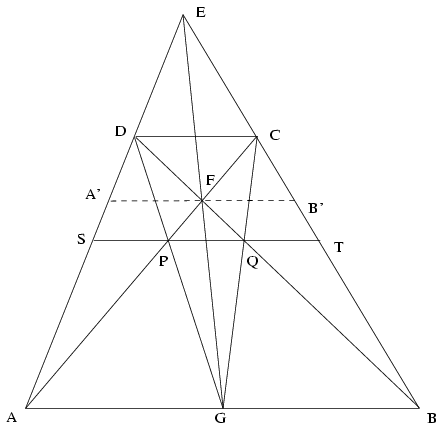
Label the vertices of the trapezium so that A,B should be the longer base and C,D should be the shorter base. Construct the intersection E of the sides AD and BC and the intersection F of the diagonals AC and BD. Consider the line through F parallel to the bases. Let A' and B' denote its intersections with the sides AD and BC, respectively. It follows easily from the equal areas of the triangles AFD and BFC that A'F=FB', as the area of triangle AFD is m^.A'F/2, and that of triangle BFC is m^.FB'/2, where m denotes the height of the trapezium. By central similitude, the line EF is also the median of triangle ABE, that is, it intersects AB at its midpoint G. The point G is easy to construct.

Construct the points P and Q where the lines DG and CG intersect the diagonals AC and BD, respectively. Now AP/PC=AG/DC=GB/DC=BQ/QD, thus P and Q divide the distance between the parallel lines AB and CD in the same ratio, that is PQ is parallel to the bases of the trapezium. Let S and T, respectively, denote the intersections of the line PQ with the sides AD and BC. Then SP/PQ=AG/GB=PQ/QT=1, that is the segment ST parallel to AB is divided by P and Q into three equal parts. Thus PQ is a line of the required property. Another line can be constructed by connecting the midpoint of DC (where line EF intersects the side DC) to the points A and B. The connecting lines intersect the diagonals at P' and Q'. With the above reasoning, it can be shown that the line P'Q' is also a solution of the problem.

It is clear that there is at most one such line on each side of the point F. As a line parallel to AB is gradually moving away from the point E, its segment between the two diagonals is growing while the other two segments are shrinking. Thus we have found all the solutions.

B.3528. Let $\displaystyle alpha$ and $\displaystyle beta$ be acute angles such that sin²$\displaystyle alpha$+sin²$\displaystyle beta$<1. Prove that sin² $alpha$ +sin²$\displaystyle beta$<sin²( $alpha$ + $beta$ ). (4 points)

Solution.

The trigonometric Pythagorean formula says that sin²$\displaystyle alpha$+sin²($\displaystyle pi$/2-$\displaystyle alpha$)=1, thus it follows from the condition that $\displaystyle beta$<$\displaystyle pi$/2-$\displaystyle alpha$, 0<$\displaystyle alpha$+$\displaystyle beta$<$\displaystyle pi$/2. As

sin²($\displaystyle alpha$+$\displaystyle beta$)=sin²$\displaystyle alpha$cos²$\displaystyle beta$+sin²$\displaystyle beta$cos²$\displaystyle alpha$+2sin$\displaystyle alpha$sin$\displaystyle beta$cos$\displaystyle alpha$cos$\displaystyle beta$ ,

the substitution of cos²x=1-sin²x and rearrangement shows that the statement is equivalent to

2sin²$\displaystyle alpha$sin²$\displaystyle beta$<2sin$\displaystyle alpha$sin$\displaystyle beta$cos$\displaystyle alpha$cos$\displaystyle beta$

Division by the positive quantity 2sin$\displaystyle alpha$sin$\displaystyle beta$ leads to the inequalities sin$\displaystyle alpha$sin$\displaystyle beta$<cos$\displaystyle alpha$cos$\displaystyle beta$, 0<cos($\displaystyle alpha$+$\displaystyle beta$) which are obviously true, as we have shown above that 0<$\displaystyle alpha$+$\displaystyle beta$<$\displaystyle pi$/2.

B.3529. The sum of the first few terms in a geometric progression is 11, the sum of their squares is 341, and the sum of their cubes is 3641. Find the terms of the sequence. (5 points)

(Suggested by Á. Besenyei, Budapest)

Solution.

Let a denote the first term of the sequence, let q be the common ratio, and let nbe the number of terms. Let Q=qⁿ. q=1 is impossible, as in that case an=11, a²n=341, and hence a=31, n=11/31, which contradicts to the condition a³n=3641 Therefore, the following relationships are true: $\displaystyle a{Q-1\over q-1}=11$

, $\displaystyle a^2{Q^2-1\over q^2-1}=341$

, $\displaystyle a^3{Q^3-1\over q^3-1}=3641.$

Divide the second and third equalities by the first one. Then $\displaystyle a{Q+1\over q+1}=31$

, $\displaystyle a^2{Q^2+Q+1\over q^2+q+-1}=331.$

Hence a(Q-1)=11(q-1) és a(Q+1)=31(q+1), thus a=10q+21 and (from a$\displaystyle ne$0) $\displaystyle Q={21q+10\over10q+21}$ can also be expressed in terms of q. Substitute the result into the equality a²(Q²+Q+1)=331(q²+q+1) above. The possible values of q are the roots of the equation 2q²+5q+2=0: q=-2 and q=-1/2. Hence either a=1, Q=-32, n=5, or a=16, Q=-1/32, n=5. Thus the solutions of the problem are the following two sequences: 1,-2,4,-8,16 and 16,-8,4,-2,1. It is easy to check that these sequences both satisfy the requirements.

B.3530. Evaluate 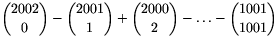${2002\choose0}-{2001\choose1}+{2000\choose2}-\dots-{1001\choose1001}$ . (5 points)

Solution. Let

$\displaystyle A_n=\sum_{i=0}^{[n/2]}(-1)^i{n-i\choose i}\ .$

for all positive integers n. The task is to determine the value of A₂₀₀₂. By using the identity $\displaystyle {n\choose k}={n-1\choose k-1}+{n-1\choose k}$, it is easy to check that A_n=A_n-1+A_n-2 for all integers n$\displaystyle ge$3: If k$\displaystyle ge$2 then

$\displaystyle A_{2k}=1+\sum_{i=1}^{k-1}(-1)^i\Bigl({2k-i-1\choose i}+{2k-i-1\choose i-1}\Bigr)+(-1)^k{k\choose k}=$

$\displaystyle =A_{2k-1}-\sum_{j=0}^{k-2}(-1)^j{2k-2-j\choose j}-(-1)^{k-1}{k-1\choose k-1}=A_{2k-1}-A_{2k-2}\ .$

If k$\displaystyle ge$1, it is even simpler, as

$\displaystyle A_{2k+1}=1+\sum_{i=1}^{k}(-1)^i\Bigl({2k-i\choose i}+{2k-i\choose i-1}\Bigr)=$

$\displaystyle =A_{2k}-\sum_{j=0}^{k-1}(-1)^j{2k-1-j\choose j}=A_{2k}-A_{2k-1}\ .$

It is easy to calculate that A₁=A₆=1, A₂=A₅=0, and A₃=A₄=-1. Hence, by induction, it can be shown that A_6k=A_6k+1=1, A_6k+2=A_6k+5=0, and A_6k+3=A_6k+4=-1 for every positive integer k. As 2002=6^.333+4, the answer is A₂₀₀₂=-1.

B.3531. The inscribed circle of a triangle ABC is centred at O, and touches the sides at A₁, B₁, C₁ (in customary notation). The lines A₁O, B₁O, C₁O intersect the segments B₁C₁, C₁A₁, A₁B₁ at the points A₂, B₂, C₂, respectively. Prove that the lines AA₂, BB₂ és CC₂ are concurrent. (5 points)

(Suggested by Á. Besenyei, Budapest)

Solution. The following statement will be used several times in the proof:

If X' is a point on the side YZ of the triangle XYZ,and $\displaystyle eta$_Y, $\displaystyle eta$_Z, $\displaystyle delta$_Y, $\displaystyle delta$_Z denote the angles XYZ, XZY, YXX', ZXX', respectively then

$\displaystyle {YX'\over ZX'}={\sin\delta_Y\over\sin\delta_Z}\cdot{\sin\eta_Z\over\sin\eta_Y}\ ,$

as it follows from the sine rule that YX'/XX'=sin$\displaystyle delta$_Y/sin$\displaystyle eta$_Y, and ZX'/XX'=sin$\displaystyle delta$_Z/sin$\displaystyle eta$_Z. In the special case of XY=XZ, $\displaystyle eta$_Y=$\displaystyle eta$_Z, and thus YX'/ZX'=sin$\displaystyle delta$_Y/sin$\displaystyle delta$_Z.

As the measures of the angles C₁A₁B₁, C₁B₁A₁, A₁C₁C₂ and B₁C₁C₂ are (with the conventional notation) ($\displaystyle beta$+$\displaystyle gamma$)/2, ($\displaystyle alpha$+$\displaystyle gamma$)/2, $\displaystyle beta$/2 and $\displaystyle alpha$/2, respectively. With the above statement, it follows that

$\displaystyle {A_1C_2\over B_1C_2}={\sin(\beta/2)\over\sin(\alpha/2)}\cdot{{\sin{\alpha+\gamma\over2}}\over{\sin{\beta+\gamma\over2}}}\ .$

Let$\displaystyle gamma$_B and $\displaystyle gamma$_A denote the angles A₁CC₂ and B₁CC₂, respectively, and let C₃ be the intersection of the line CC₂ with the segment AB. By using CA₁=CB₁ and using the above statement again, we have

$\displaystyle {AC_3\over C_3B}={\sin\gamma_A\over\sin\gamma_B}\cdot{\sin\beta\over\sin\alpha}={B_1C_2\over A_1C_2}\cdot{\sin\beta\over\sin\alpha}={\sin(\alpha/2)\over\sin(\beta/2)}\cdot{\sin{\beta+\gamma\over2}\over{\sin{\alpha+\gamma\over2}}}\cdot{\sin\beta\over\sin\alpha}\ .$

Similarly,

$\displaystyle {BA_3\over A_3C}={\sin(\beta/2)\over\sin(\gamma/2)}\cdot{\sin{\gamma+\alpha\over2}\over{\sin{\beta+\alpha\over2}}}\cdot{\sin\gamma\over\sin\beta}$

and

$\displaystyle {CB_3\over B_3A}={\sin(\gamma/2)\over\sin(\alpha/2)}\cdot{\sin{\alpha+\beta\over2}\over{\sin{\gamma+\beta\over2}}}\cdot{\sin\alpha\over\sin\gamma}\ ,$

where A₃ and B₃ denote the intersections of the lines AA₂ and BB₂ with the sides BC and AC, respectively. Therefore, by putting all together we get

$\displaystyle {AC_3\over C_3B}\cdot{BA_3\over A_3C}\cdot{CB_3\over B_3A}=1\ ,$

and thus the statement of the problem follows immediately from Ceva's theorem.

Already signed up?
New to KöMaL?