A 2002. februári B-jelű matematika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

B. 3522. Oldjuk meg az egész számok körében a

2x⁴+x²y²+5y²=y⁴+10x²

egyenletet. (3 pont)

Megoldás. Ha A=x² és B=y², akkor átrendezés és szorzattá alakítás után az egyenlet a (2A-B)(A+B-5)=0 alakot ölti. Tehát vagy 2x²=y², ahonnan x=y=0 adódik, vagy pedig x²+y²=5. Ezért az egyenletnek 9 megoldása van, mégpedig x=y=0, x=$\displaystyle pm$2,y=$\displaystyle pm$1, valamint x=$\displaystyle pm$1,y=$\displaystyle pm$2.

B. 3523. Adott egy félkör. Tekintsük azokat a háromszögeket, amelyek egyik oldala tartalmazza a félkör átmérőjét, másik két oldala pedig érinti a félkört. E háromszögek közül melyiknek legkisebb a területe? (4 pont)

Megoldás. Ha a háromszöget tükrözzük az átmérőt tartalmazó oldal egyenesére, akkor egy olyan deltoidot kapunk, amelynek oldalai érintik az adott kört. Azt állítjuk, hogy ezen deltoidok közül a négyzetnek lesz a legkisebb a területe. Ebből következik, hogy a tekintett háromszögek közül annak az egyenlő szárú derékszögű háromszögnek lesz a legkisebb a területe, amelynek átfogója tartalmazza a félkör átmérőjét. Általánosabban, megmutatjuk, hogy egy adott kört érintő négyszögek közül a négyzetnek a legkisebb a területe. Legyen a kör sugara egységnyi, és tekintsünk egy olyan négyszöget, melynek oldalai érintik a kört, szögei pedig rendre $\displaystyle pi$-2$\displaystyle alpha$,$\displaystyle pi$-2$\displaystyle beta$,$\displaystyle pi$-2$\displaystyle gamma$,$\displaystyle pi$-2$\displaystyle delta$ nagyságúak, ahol az $\displaystyle alpha$,$\displaystyle beta$,$\displaystyle gamma$,$\displaystyle delta$ hegyesszögek összege $\displaystyle pi$. Ekkor a négyszög területe

$\displaystyle \tan\alpha+\tan\beta+\tan\gamma+\tan\delta\le4\tan\Bigl({\alpha+\beta+\gamma+\delta\over4}\Bigr)=4\tan(\pi/4)=4\ ,$

ugyanis a tangens függvény a (0,$\displaystyle pi$/2) intervallumban alulról szigorúan konvex. Ugyanezért egyenlőség csak az $\displaystyle alpha$=$\displaystyle beta$=$\displaystyle gamma$=$\displaystyle delta$=$\displaystyle pi$/4 esetben állhat fenn, vagyis ha a négyszög minden szöge derékszög. Ez bizonyítja állításunkat.

B. 3524. Az x, y valós számok összege 1. Határozzuk meg xy⁴+x⁴y legnagyobb értékét. (3 pont) Megoldás. Tekintve, hogy

xy⁴+x⁴y=xy(x³+y³)=xy((x+y)³-3xy(x+y))=xy(1-3xy) ,

feladatunk az A(1-3A) kifejezés maximumának megkeresése azon feltétel mellett, hogy az A szám x(1-x) alakba írható. Minthogy

$\displaystyle A(1-3A)={1\over12}-3\Bigl(A-{1\over6}\Bigr)^2\ ,$

az A(1-3A) kifejezés a maximumát az A=1/6 helyen veszi fel, a maximum értéke pedig 1/12. Az x(1-x)=1/6 másodfokú egyenlet megoldásából adódik, hogy ha $\displaystyle x=(1\pm\sqrt{1/3})/2$, akkor A=1/6=x(1-x). Ezért az A(1-3A) kifejezés maximuma az adott feltétel mellett is 1/12 lesz.

B. 3525. Bizonyítsuk be, hogy az 1,31,331,3331,... sorozatban végtelen sok összetett szám van. (4 pont)

Megoldás. 31 prímszám, ezért a kis Fermat tétel értelmében 31 osztója a 10³⁰-1 számnak, és ennek következtében az összes 10^30k-1 alakú számnak is, ahol k pozitív egész. Osztója tehát ezen számok harmadrészének is, vagyis minden olyan számnak, ami 30k darab 3-as számjegyből áll. Egy ilyen számot 100-zal megszorozva, majd az eredményhez 31-et hozzáadva újfent 31-gyel osztható számhoz jutunk, és minden ilyen szám a megadott sorozathoz tartozik. Összefoglalva, 31-től kezdve a sorozat minden 30-adik eleme 31-gyel osztható, tehát (a 31 kivételével) összetett szám.

B. 3526. Az ABCD téglalap BC oldalának felezőpontja F, CD oldalának a C-hez közelebbi harmadolópontja H. Milyen nagy lehet a HAF szög? (4 pont)

Megoldás.

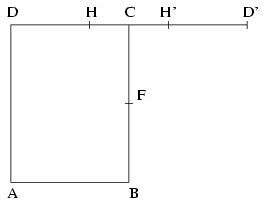
Rögzítsük a D és C pontokat, és jelölje D' és H' a D, illetve H pont tükörképét C-re. Képzeljük el, hogy a HAF szög $\displaystyle gamma$ nagysága adott, és próbáljuk meg megkeresni az A pont helyét. Az A pont egyrészt a D-ben DC-re emelt merőlegesen helyezkedik el, másrészt egy olyan $\displaystyle gamma$ szögű látóköríven, melynek két végpontja éppen H és D', a kör középpontja pedig a CD egyenesre H'-ben emelt merőlegesre esik. A kör sugara tehát legalább DH'=HD' kell legyen, ebben az esetben a HD' szakaszhoz tartozó középponti szög $\displaystyle pi$/3, $\displaystyle gamma$=$\displaystyle pi$/6. Ha a kör sugarát növeljük, akkor $\displaystyle gamma$ értéke folytonosan csökkenve 0-hoz tart, és minden esetben az A pont megszerkeszthető. Következésképpen a HAF szög nagysága tetszőleges $\displaystyle pi$/6-nál nem nagyobb pozitív érték lehet.

B. 3527. Adott egy trapéz, melynek a szárai nem párhuzamosak. Szerkesszünk csak vonalzóval olyan egyenest, amelynek a trapéz szárai közé eső szakaszát a trapéz átlói harmadolják. (5 pont)

Megoldás.

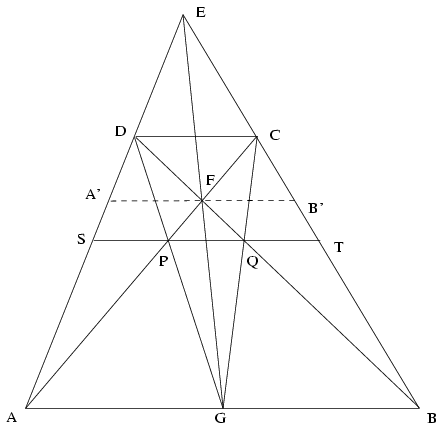
Betűzzük meg úgy a trapéz csúcsait, hogy a hosszabb alap csúcsai legyenek A,B, a rövidebbiké pedig C,D. Az AD és BC szárak egyenésenek E metszéspontját, valamint az AC és BD átlók F metszéspontját könnyen megszerkeszthetjük. Húzzunk képzeletben párhuzamost az F ponton keresztül a trapéz oldalaival, és jelölje A' és B' azt a két pontot, ahol ez az egyenes az AD, illetve BC szárat metszi. Közismert, és könnyen levezethető az AFD és BFC háromszögek területének egyenlőségéből az, hogy A'F=FB', hiszen az AFD háromszög területe m^.A'F/2, a BFC háromszögé pedig m^.FB'/2, ahol m a trapéz magasságát jelöli. A párhuzamos szelők tételéből következik, hogy az EF egyenes az ABE háromszögnek is súlyvonala, tehát az AB oldal G felezőpontjában metszi az AB egyenest. Ez a G pont tehát könnyen megszerkeszthető.

Szerkesszük meg azon P és Q pontokat, ahol a DG és CG egyenes a AC, illetve BD átlót metszi. Ekkor AP/PC=AG/DC=GB/DC=BQ/QD, tehát a P és a Q pont ugyanolyan arányban osztja az egymással párhuzamos AB és CD egyenesek közötti távolságot, vagyis PQ párhuzamos az trapéz alapjaival. Jelölje a PQ egyenesnek az AD és BC szárakkal alkotott metszéspontját S, illetve T. Ekkor SP/PQ=AG/GB=PQ/QT=1, vagyis P és Q az AB-vel párhuzamos ST szakasz harmadolópontjai. Az egyik keresett egyenes tehát PQ. Egy további egyenest úgy szerkeszthetünk meg, hogy a DC szakasz felezőpontját, melyet az EF egyenes metsz ki a BC oldalból, összekötjük az A és a B pontokkal, és az így keletkező egyeneseket metsszük el a trapéz átlóival. Az így keletkező P' és Q' pontokra az előbbi bizonyítás mintájára igazolhatjuk, hogy a P'Q' egyenes is megoldása a feladatnak.

Világos, hogy az F pont mindkét oldalán legfeljebb egy ilyen egyenes talalható, hiszen ahogy az AB-vel párhuzamos egyenest az E ponttól távolítjuk, úgy a két átló közé eső szakasz hossza nő, a másik két szakasz hossza pedig csökken. Ezzel tehát a feladat összes megoldását meghatároztuk.

B. 3528. Legyenek $\displaystyle alpha$ és $\displaystyle beta$ olyan hegyesszögek, amelyekre sin²$\displaystyle alpha$+sin²$\displaystyle beta$<1. Bizonyítsuk be, hogy sin²$\displaystyle alpha$+sin²$\displaystyle beta$<sin²(+). (4 pont)

Megoldás. A trigonometrikus Pithagorasz tétel szerint sin²$\displaystyle alpha$+sin²($\displaystyle pi$/2-$\displaystyle alpha$)=1, ezért a feltételből adódik, hogy $\displaystyle beta$<$\displaystyle pi$/2-$\displaystyle alpha$, 0<$\displaystyle alpha$+$\displaystyle beta$<$\displaystyle pi$/2. Mivel

sin²($\displaystyle alpha$+$\displaystyle beta$)=sin²$\displaystyle alpha$cos²$\displaystyle beta$+sin²$\displaystyle beta$cos²$\displaystyle alpha$+2sin$\displaystyle alpha$sin$\displaystyle beta$cos$\displaystyle alpha$cos$\displaystyle beta$ ,

cos²x=1-sin²x helyettesítés és rendezés után látható, hogy a bizonyítandó állítás a

2sin²$\displaystyle alpha$sin²$\displaystyle beta$<2sin$\displaystyle alpha$sin$\displaystyle beta$cos$\displaystyle alpha$cos$\displaystyle beta$

állítással ekvivalens. A pozitív 2sin$\displaystyle alpha$sin$\displaystyle beta$ mennyiséggel elosztva, az ezzel ekvivalens sin$\displaystyle alpha$sin$\displaystyle beta$<cos$\displaystyle alpha$cos$\displaystyle beta$, 0<cos($\displaystyle alpha$+$\displaystyle beta$) egyenlőtlenségekhez jutunk, ez utóbbi pedig nyilván fennáll a fent levezetett 0<$\displaystyle alpha$+$\displaystyle beta$<$\displaystyle pi$/2 egyenlőtlenség miatt.

B. 3529. Egy mértani sorozat első néhány tagjának összege 11, négyzetösszegük 341, köbösszegük 3641. Határozzuk meg a sorozat tagjait. (5 pont)

Javasolta: Besenyei Ádám, Budapest

Megoldás. Jelölje a sorozat első elemét a, hányadosát q, tagjainak számat pedig n. Legyen továbbá Q=qⁿ. Az nem lehet, hogy q=1, mert ekkor an=11, a²n=341 miatt a=31, n=11/31 lenne, ellentmondva az a³n=3641 feltételnek. Ezért a következő összefüggéseket írhatjuk föl:

$$ A második és harmadik összefüggést az elsővel elosztva kapjuk továbbá, hogy

$\displaystyle a{Q+1\over q+1}=31\ ,\ \ a^2{Q^2+Q+1\over q^2+q+-1}=331\ .$

Felírhatjuk tehát, hogy a(Q-1)=11(q-1) és a(Q+1)=31(q+1), ahonnan a=10q+21 és (a$\displaystyle ne$0 miatt) $\displaystyle Q={21q+10\over10q+21}$ is q segítségével kifejezhető. Ezt a fent levezetett a²(Q²+Q+1)=331(q²+q+1) összefüggésbe beírva végül a 2q²+5q+2=0 egyenlethez jutunk, ahonnan q lehetséges értékeire q=-2 és q=-1/2 adódik. Ennek megfelelően kapjuk, hogy a=1, Q=-32, n=5, illetve a=16, Q=-1/32, n=5. A feladat megoldása tehát a következő két sorozat (melyekről könnyen ellenőrizhetjük, hogy valóban kielégítik a feltételeket): 1,-2,4,-8,16, illetve 16,-8,4,-2,1.

B. 3530. Számítsuk ki $\displaystyle {2002\choose0}-{2001\choose1}+{2000\choose2}-\dots-{1001\choose1001}$ értékét. (5 pont)

Megoldás. Legyen minden n pozitív egészre

$\displaystyle A_n=\sum_{i=0}^{[n/2]}(-1)^i{n-i\choose i}\ .$

Feladatunk A₂₀₀₂ értékének meghatározása. Az $\displaystyle {n\choose k}={n-1\choose k-1}+{n-1\choose k}$ azonosság (n$\displaystyle ge$k$\displaystyle ge$1) segítségével könnyen ellenőrizhetjük, hogy minden n$\displaystyle ge$3 egész számra A_n=A_n-1+A_n-2. Valóban, ha k$\displaystyle ge$2, akkor

$\displaystyle A_{2k}=1+\sum_{i=1}^{k-1}(-1)^i\Bigl({2k-i-1\choose i}+{2k-i-1\choose i-1}\Bigr)+(-1)^k{k\choose k}=$

$\displaystyle =A_{2k-1}-\sum_{j=0}^{k-2}(-1)^j{2k-2-j\choose j}-(-1)^{k-1}{k-1\choose k-1}=A_{2k-1}-A_{2k-2}\ ,$

ha pedig k$\displaystyle ge$1, akkor még egy kicsit egyszerűbben

$\displaystyle A_{2k+1}=1+\sum_{i=1}^{k}(-1)^i\Bigl({2k-i\choose i}+{2k-i\choose i-1}\Bigr)=$

$\displaystyle =A_{2k}-\sum_{j=0}^{k-1}(-1)^j{2k-1-j\choose j}=A_{2k}-A_{2k-1}\ .$

Könnyen kiszámolhatjuk, hogy A₁=A₆=1, A₂=A₅=0, és A₃=A₄=-1. Innen pedig teljes indukcióval könnyen ellenőrizhető, hogy minden k pozitív egészre A_6k=A_6k+1=1, A_6k+2=A_6k+5=0, és A_6k+3=A_6k+4=-1. Mivel 2002=6^.333+4, a keresett érték A₂₀₀₂=-1.

B. 3531. Az ABC háromszög O középpontú beírt körének az oldalakon levő érintési pontjai (a szokásos jelölésekkel) A₁, B₁, C₁. Az A₁O, B₁O, C₁O egyenesek rendre az A₂, B₂, C₂ pontokban metszik a B₁C₁, C₁A₁, A₁B₁ szakaszokat. Bizonyítsuk be, hogy az AA₂, BB₂ és CC₂ egyenesek egy ponton mennek át. (5 pont)

Javasolta: Besenyei Ádám, Budapest

Megoldás. A megoldás során több ízben fel fogjuk használni a következő állítást: ha X' az XYZ háromszög YZ oldalának pontja, és az XYZ, XZY, YXX' és ZXX' szögeket rendre $\displaystyle eta$_Y, $\displaystyle eta$_Z, $\displaystyle delta$_Y, illetve $\displaystyle delta$_Z jelöli, akkor

$\displaystyle {YX'\over ZX'}={\sin\delta_Y\over\sin\delta_Z}\cdot{\sin\eta_Z\over\sin\eta_Y}\ ,$

ugyanis a szinusz tétel miatt egyrészt YX'/XX'=sin$\displaystyle delta$_Y/sin$\displaystyle eta$_Y, másrészt ZX'/XX'=sin$\displaystyle delta$_Z/sin$\displaystyle eta$_Z. Speciálisan, ha XY=XZ, akkor $\displaystyle eta$_Y=$\displaystyle eta$_Z, és így YX'/ZX'=sin$\displaystyle delta$_Y/sin$\displaystyle delta$_Z.

Mivel a C₁A₁B₁, C₁B₁A₁, A₁C₁C₂ és B₁C₁C₂ szögek nagysága, a szokásos jelölésekkel élve, rendre ($\displaystyle beta$+$\displaystyle gamma$)/2, ($\displaystyle alpha$+$\displaystyle gamma$)/2, $\displaystyle beta$/2, illetve $\displaystyle alpha$/2, a fenti állítás értelmében

$\displaystyle {A_1C_2\over B_1C_2}={\sin(\beta/2)\over\sin(\alpha/2)}\cdot{{\sin{\alpha+\gamma\over2}}\over{\sin{\beta+\gamma\over2}}}\ .$

Jelölje az A₁CC₂ és B₁CC₂ szögeket rendre $\displaystyle gamma$_B és $\displaystyle gamma$_A, és legyen C₃ a CC₂ egyenesnek az AB szakasszal alkotott metszéspontja. Figyelembe véve, hogy CA₁=CB₁, a megoldás elején tett észrevételünk ismételt alakalmazásával nyerjük, hogy

$\displaystyle {AC_3\over C_3B}={\sin\gamma_A\over\sin\gamma_B}\cdot{\sin\beta\over\sin\alpha}={B_1C_2\over A_1C_2}\cdot{\sin\beta\over\sin\alpha}={\sin(\alpha/2)\over\sin(\beta/2)}\cdot{\sin{\beta+\gamma\over2}\over{\sin{\alpha+\gamma\over2}}}\cdot{\sin\beta\over\sin\alpha}\ .$

Hasonlóképpen kapjuk, hogy

$\displaystyle {BA_3\over A_3C}={\sin(\beta/2)\over\sin(\gamma/2)}\cdot{\sin{\gamma+\alpha\over2}\over{\sin{\beta+\alpha\over2}}}\cdot{\sin\gamma\over\sin\beta}$

és

$\displaystyle {CB_3\over B_3A}={\sin(\gamma/2)\over\sin(\alpha/2)}\cdot{\sin{\alpha+\beta\over2}\over{\sin{\gamma+\beta\over2}}}\cdot{\sin\alpha\over\sin\gamma}\ ,$

ahol A₃ és B₃ az AA₂ és BB₂ egyneseknek a BC, illetve AC oldallal alkotott metszéspontját jelölik. Mindent összevetve láthatjuk, hogy

$\displaystyle {AC_3\over C_3B}\cdot{BA_3\over A_3C}\cdot{CB_3\over B_3A}=1\ ,$

és így a bizonyítandó állítás közvetlenül leolvasható Ceva tételéből.