A 2002. februári számban kitűzött fizika elméleti feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

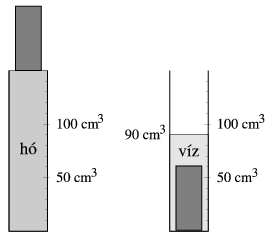
P. 3498.A mérőhengert friss hóval töltjük meg, majd a hó felszínére helyezünk egy 162 g tömegű alumíniumhengert, s megvárjuk, míg az összes hó megolvad (lásd a jobb oldali ábrát). Mennyi a hó sűrűsége? (3 pont)

Jedlik Ányos verseny, Nyíregyháza

Megoldás. 200 kg/m³

P. 3499.Gáztűzhelyen egy lábasban vizet melegítünk. Változik-e bármennyit is a lábas alján a víz hidrosztatikai nyomása? (3 pont)

Tarján Imre emlékverseny, Szolnok

Megoldás. Igen. A lábos maga is tágul, az aljának a felülete nő, így a nyomás csökken.

P. 3500. Egy hegymászó két, egymással párhuzamos, függőleges sziklafalnak támaszkodik úgy, hogy az egyik falnak a bakancsát, a másiknak pedig a hátát nyomja. A súrlódási együttható a bakancs talpa és a sziklafal között 1,2, a hegymászó háta és a fal között 0,8. Legalább mekkora erővel kell nyomnia a falat? Készítsünk ábrát! (5 pont)

A Lánczos Kornél verseny nyomán

P. 3500. Megoldás. Ha a hegymászó lábával F erővel nyomja az egyik falat, a háta is ennyivel nyomja a másikat. A bakancs és a fal közt hasson S₁, a mászó háta és a fal közt pedig S₂ súrlódási erő. Egyensúly esetén

G=S₁+S₂$\displaystyle \le$($\displaystyle \mu$₁+$\displaystyle \mu$₂)F .

Innen F$\displaystyle \ge$G/($\displaystyle \mu$₁+$\displaystyle \mu$₂)=G/2. Várhatóan ennél nagyobb erővel kell nyomnia a falat: mivel a mászó súlypontja vélhetőleg közelebb van a hátához, mint a lábfejéhez, a forgatónyomatékok egyensúlya megkívánja, hogy az S₂>S₁ legyen (hogy pontosan mennyiszer, az a hegymászó testhelyzetétől függ), következésképpen F is nagyobb, mint G/2.

P. 3501. Az ábrán látható elrendezésben a vízszintes asztalon két, kezdetben nyújtatlan, párhuzamos helyzetű, D direkciós erejű gumiszálra könnyen csúszó, m tömegű gyűrűt fűzünk. A gyűrűt az egyensúlyi helyzetéből lassan

a) az A pontba,

b) a B pontba visszük.

Mekkora munkát végzünk, és mekkora gyorsulással indul a gyűrű elengedés után az egyes esetekben? Az asztalon a gyűrű súrlódásmentesen mozoghat. (Adatok: a=0,1 m; b=1 m; D=150 N/m; m=0,1 kg.) (5 pont)

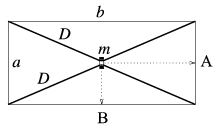
Közli: Sári Péter, Budapest

Megoldás. Az alaphelyzetben a gumikban tárolt rugalmas energia E₀=3,75^.10^-3 J.

a) A végzett munka L_A=0,39 J, és az induló gyorsulás a_A=154 m/s².

b) A végzett munka L_B=2,57^.10^-2 J, és az induló gyorsulás a_B=11,7 m/s².

P. 3502. Egy úszó tengeralattjáró térfogatának 10%-a van a vízfelszín felett. Ekkor térfogatának 80%-ában levegő van. Egy baleset után térfogatának már csak 10%-ában maradt (zárt kamrákban) levegő, s a 18 300 m³ térfogatú tengeralattjáró 110 méter mélyre süllyedt. Mekkora munkával lehet kiemelni onnan? (A tengervíz sűrűsége 1030 kg/m³). (4 pont)

Közli: Simon Péter, Pécs

Megoldás. A tengeralattjáró tömege M=0,9V$\displaystyle \rho$. Az elsüllyedés során a tengeralattjáróba még m=0,7V$\displaystyle \rho$ víz folyik. Összesen tehát (M+m)g= súlyt kell felhozni, miközben a felhajtóerő F=V$\displaystyle \rho$g. Így a szükséges munka

(0,9+0,7-1)V$\displaystyle \rho$gh=0,6^.18 300^.1030^.10^.110=1,24^.10¹⁰ J.

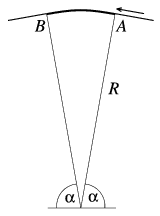
P. 3503. Egy kis hídon az úttest egy R=100 m sugarú, függőleges síkú kör 180^o-2 szögű köríve mentén fekszik ($\displaystyle alpha$=80^o). Egy motoros az A pontban akkora sebességgel fut fel a hídra, hogy ,,elszáll''. Legalább mennyi ekkor a sebessége? Mekkora sebesség esetén érne vissza az útra a B pontban? (4 pont)

Közli: Lévai Albert, Mezőtúr

Megoldás. A motoros az A pontban elrepül, ha

$\displaystyle v\geq\sqrt{gR\sin\alpha}=31{,}1~{\rm m/s}=112~{\rm km/h}.$

Ha az elszállt motoros a B pontban ér földet, sebessége

$\displaystyle v_1=\sqrt{gR\over\sin\alpha}=31{,}5~{\rm m/s}=114~ {\rm km/h}.$

P. 3504.Levegővel az ábrán látható ABCA körfolyamatot végeztetjük egy termodinamikai gépben. Milyen ez a gép: hőerőgép, vagy hűtőgép? Hányszorosa az AB szakaszon felvett hő a CA szakaszon leadott hőnek? (5 pont)

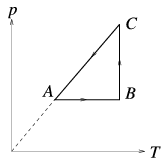
Közli: Légrádi Imre, Sopron

Megoldás. A folyamatok az egyes szakaszokon:

A$\displaystyle \rightarrow$B: izobár tágulás, a hőfelvétel Q_AB=c_p(T_B-T_A).

B$\displaystyle \rightarrow$C: izoterm összenyomás, a gáz a rajta végzett munkát hő formájában leadja.

B$\displaystyle \rightarrow$A: izochor hűtés, a hőleadás -Q_CA=c_v(T_B-T_A).

Ez a berendezés hűtőgépként működik (a magas hőmérsékletű állapotban hőt ad le; az egy ciklusban a rendszeren végzett munka pozitív), és

$\displaystyle {Q_{AB}\over\vert Q_{CA}\vert}={c_p\over c_v}=1{,}40.$

P. 3505.A síkkondenzátor széleinél inhomogén elektromos mező alakul ki, de ezt általában el szoktuk hanyagolni. Nagyobb vagy kisebb értéket kapnánk a kapacitás nagyságára, ha ezt a tényt is figyelembe vennénk? (5 pont)

Közli: Varga István, Békéscsaba

Bay Zoltán verseny, Sarkad

Megoldás. A kapacitás definíció szerint C=Q/U. A számolásoknál feltételezett szórt tér nélküli esetben a fegyverzetek közötti elektromos tér nagyobb, mint valójában (az erővonalak - melyek ,,számát'' a Q meghatározza - a kisebb térben sűrűbben vannak), így a lemezek közötti feszültséget is nagyobbnak mutatja a közelítő számítás. A számított kapacitás tehát kisebb, mint a tényleges.

P. 3506.Négy sorbakapcsolt ,,laposelemből'' álló telep elektromotoros ereje 18 V. A rákapcsolt fogyasztón 0,3 A folyik, amely azonban 0,2 A-re csökken, ha a fogyasztóval párhuzamosan egy 8 $\displaystyle Omega$-os ellenállást is kötünk a telepre. Mekkora egyetlen ,,laposelem'' belső ellenállása? (4 pont)

Közli: Holics László, Budapest

Megoldás. Jelölje R a fogyasztó ellenállását, R_b a kérdéses belső ellenállást, és legyen I a 8$\displaystyle \Omega$-os ,,söntön'' átfolyó áram. A két kapcsolásra felírható egyenletek:

18V=0,3 A^.(4R_b+R) ,

illetve

18 V=(0,2 A+I)^.4R_b+0,2 A^.R,

I^.8 $\displaystyle \Omega$=0,2 A^.R.

Az egyenletrendszernek két megoldása van: R_b=1,08 $\displaystyle \Omega$  (R=55,7 $\displaystyle \Omega$), illetve R_b=14 $\displaystyle \Omega$  (R=4,31 $\displaystyle \Omega$).

P. 3507.Milyen esetekben fordulhat elő, hogy egy kétszer domború (,,bikonvex'') üveglencsére eső párhuzamos sugárnyaláb ugyancsak párhuzamos nyalábként hagyja el a lencsét? (5 pont)

Közli: Radnai Gyula, Budapest

Megoldás. Ha a lencse vastagsága (r₁+r₂)n/(n-1). (Itt r_1,2 a két felület görbületi sugara, n pedig a törésmutató.) Ilyenkor az egyik oldalon belépő nyaláb még a lencse belsejében fókuszálódik, mégpedig éppen ott, ahonnan kiindulva a másik felület éppen párhuzamosítja.

Egy másik (nyilvánvaló) megoldás: ha az üveglencsét olyan folyadék veszi körül, amelynek törésmutatója megegyezik az üvegével.

P. 3508.Egy $\displaystyle lambda$ hullámhosszúságú foton ütközik egy nyugvónak és szabadnak tekinthető elektronnal. A kölcsönhatás során az elektron meglökődik, s egy 2$\displaystyle lambda$ hullámhosszúságú foton indul a beesővel ellentétes irányba. Határozzuk meg a beeső foton hullámhosszát! (5 pont)

Közli: Szegedi Ervin, Debrecen

Nagy László verseny, Kazincbarcika

Megoldás. A meglökött elektron által kapott impulzus és energia

$\displaystyle p=mv={m_0v\over\sqrt{1-\left({v\over c}\right)^2}}={3h\over2\lambda}\,,$

$\displaystyle mc^2-m_0c^2 ={m_0c^2\over\sqrt{1-\left({v\over c}\right)^2}}-m_0c^2= {hc\over2\lambda}\,.$

E két egyenlet megoldása:

$\displaystyle {v\over c}=0{,}6\,$, $\displaystyle \lambda={2h\over m_0c}=4{,}85\cdot10^{-12}~{\rm m}\,$.