Exercises and problems in Physics
February 2002
Please read The Conditions of the Problem Solving Competition.
 |
Experimental problem |
M. 231. With the help of measurements determine what the dependence of the warming rate of a glass of water in a microwave oven on the amount of water in the glass, on the size of the glass and on its position on the center plate is! (6 points)
 |
Theoretical problems |
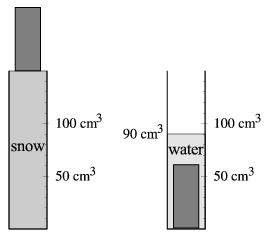
P. 3498.Fill a graduated cylinder with fresh snow, and put on the surface of the snow an aluminum cylinder of a mass of 162 g and wait until all the snow melts. (See the figure on the right.) What is the density of the snow? (3 points)
P. 3499. While heating up some water in a pot on a gas-cooker does the hydrostatic pressure of the water change at the bottom? (3 points)
P. 3500. A climber sits between two parallel rock walls so that he presses his boots to one and his back to the other wall. The friction coefficient between the boots and the wall is 1.2 and between the wall and the climber's back is 0.8. What force does he need to apply on the wall at least? Draw a figure. (5 points)
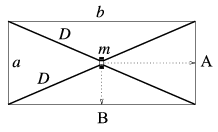
P. 3501. In the arrangement seen in the figure, lying on a horizontal table two parallel, unstretched rubber threads of spring constant D are going through a ring of mass m, which can easily slip along them. We take the ring from its state of equilibrium to a) point A, b) point B. What is the amount of work done and what is the starting acceleration of the ring in the two cases? The ring can move along the table fricitionless. (Data: a=0.1 m; b=1 m; D=150 N/m; m=0.1 kg.) (5 points)
P. 3502. 10% of the volume of a floating submarine is above the water level. In this case 80% of its volume is filled with air. After an accident the amount of air drops to 10% (in closed chambers) and the 18 300 m3 volume submarine sinks to a 110 m depth. How much work is needed to salvage the submarine? (The density of the sea water is 1030 kg/m3.) (4 points)
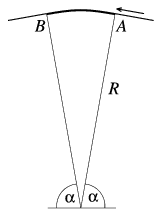
P. 3503. On a small bridge the road runs along a
circle arc of radius R and of 180o-2
angle lying in
a vertical plane. A motorcyclist runs up the bridge with such a
velocity that he flies off the road. What is its velocity at least? At
what velocity would he touch the road again in point B? (Data:
R=100 m; \(\displaystyle alpha\)=80o.) (4 points)
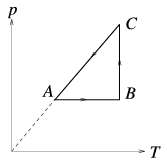
P. 3504. We perform the ABCA cycle seen in the figure with air as medium in a thermodynamical machine. Is this machine a heat engine or a refrigerator? What is the ratio of the absorbed heat in section AB and the emitted heat in section CA? (5 points)
P. 3505. At the edge of a plate capacitor there is an inhomogeneous electric field, which is usually neglected. Taking this into account as well, would we get a smaller or a greater capacity value? (5 points)
P. 3506. The electromotive force of a power
source consisting of four serially connected 4.5V batteries is
18 V. A connected consumer carries an electric current of
0.3 A. This current decreases to 0.2 A if an 8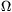 
resistance is
connected parallel to the power source. What is the internal
resistance of one 4.5V battery? (4 points)
P. 3507. In what cases does a parallel light beam incident on a double-convex (``biconvex'') glass lens keep parallel after leaving the lens? (5 points)
P. 3508. A \(\displaystyle lambda\) wavelength photon collides with an electron, which can be considered resting and free. In the interaction the electron recoils and a 2\(\displaystyle lambda\) wavelength photon starts in the opposite direction of the incident one. Determine the wavelength of the incident photon. (5 points)
Send your solutions to the following address:
- KöMaL Szerkesztőség (KöMaL feladatok),
Budapest 112, Pf. 32. 1518, Hungary