Fizikából kitűzött gyakorlatok és feladatok
2002. február

Kérjük, olvassa el a versenykiírást.

Mérési feladat

M. 231.Mérjük meg, hogyan függ a mikrohullámú sütőben egy pohárban levő víz melegedésének sebessége a víz mennyiségétől, a pohár méreteitől és a forgótányéron elfoglalt helyétől! (6 pont)

Közli: Kaufmann Zoltán, Budapest

Az elméleti versenyben kitűzött gyakorlatok és feladatok Az elméleti fizika feladatokra kapható pontszám a feladatok nehézségétől függ. Az 1-8. osztályosok versenyében minden hónapban a 3 legnagyobb, a 9-12. osztályosok versenyeiben minden hónapban az 5 legnagyobb pontszám számít be a pontversenybe.

P. 3498.A mérőhengert friss hóval töltjük meg, majd a hó felszínére helyezünk egy 162 g tömegű alumíniumhengert, s megvárjuk, míg az összes hó megolvad (lásd a jobb oldali ábrát). Mennyi a hó sűrűsége? (3 pont)

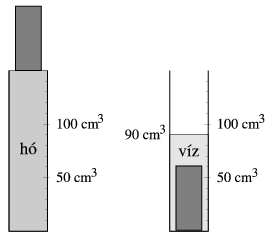
Jedlik Ányos verseny, Nyíregyháza

P. 3499.Gáztűzhelyen egy lábasban vizet melegítünk. Változik-e bármennyit is a lábas alján a víz hidrosztatikai nyomása? (3 pont)

Tarján Imre emlékverseny, Szolnok

P. 3500. Egy hegymászó két, egymással párhuzamos, függőleges sziklafalnak támaszkodik úgy, hogy az egyik falnak a bakancsát, a másiknak pedig a hátát nyomja. A súrlódási együttható a bakancs talpa és a sziklafal között 1,2, a hegymászó háta és a fal között 0,8. Legalább mekkora erővel kell nyomnia a falat? Készítsünk ábrát! (5 pont)

A Lánczos Kornél verseny nyomán

P. 3501. Az ábrán látható elrendezésben a vízszintes asztalon két, kezdetben nyújtatlan, párhuzamos helyzetű, D direkciós erejű gumiszálra könnyen csúszó, m tömegű gyűrűt fűzünk. A gyűrűt az egyensúlyi helyzetéből lassan

a) az A pontba,

b) a B pontba visszük.

Mekkora munkát végzünk, és mekkora gyorsulással indul a gyűrű elengedés után az egyes esetekben? Az asztalon a gyűrű súrlódásmentesen mozoghat. (Adatok: a=0,1 m; b=1 m; D=150 N/m; m=0,1 kg.) (5 pont)

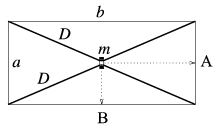
Közli: Sári Péter, Budapest

P. 3502. Egy úszó tengeralattjáró térfogatának 10%-a van a vízfelszín felett. Ekkor térfogatának 80%-ában levegő van. Egy baleset után térfogatának már csak 10%-ában maradt (zárt kamrákban) levegő, s a 18 300 m³ térfogatú tengeralattjáró 110 méter mélyre süllyedt. Mekkora munkával lehet kiemelni onnan? (A tengervíz sűrűsége 1030 kg/m³). (4 pont)

Közli: Simon Péter, Pécs

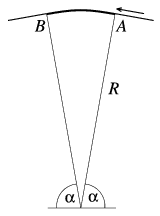
Egy kis hídon az úttest egy R=100 m sugarú, függőleges síkú kör 180^o-2\(\displaystyle alpha\) szögű köríve mentén fekszik (=80^o). Egy motoros az A pontban akkora sebességgel fut fel a hídra, hogy ,,elszáll''. Legalább mennyi ekkor a sebessége? Mekkora sebesség esetén érne vissza az útra a B pontban? (4 pont)

Közli: Lévai Albert, Mezőtúr

P. 3504.Levegővel az ábrán látható ABCA körfolyamatot végeztetjük egy termodinamikai gépben. Milyen ez a gép: hőerőgép, vagy hűtőgép? Hányszorosa az AB szakaszon felvett hő a CA szakaszon leadott hőnek? (5 pont)

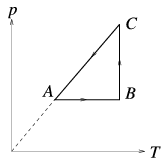
Közli: Légrádi Imre, Sopron

P. 3505.A síkkondenzátor széleinél inhomogén elektromos mező alakul ki, de ezt általában el szoktuk hanyagolni. Nagyobb vagy kisebb értéket kapnánk a kapacitás nagyságára, ha ezt a tényt is figyelembe vennénk? (5 pont)

Közli: Varga István, Békéscsaba

Bay Zoltán verseny, Sarkad

P. 3506.Négy sorbakapcsolt ,,laposelemből'' álló telep elektromotoros ereje 18 V. A rákapcsolt fogyasztón 0,3 A folyik, amely azonban 0,2 A-re csökken, ha a fogyasztóval párhuzamosan egy 8 \(\displaystyle Omega\)-os ellenállást is kötünk a telepre. Mekkora egyetlen ,,laposelem'' belső ellenállása? (4 pont)

Közli: Holics László, Budapest

P. 3507.Milyen esetekben fordulhat elő, hogy egy kétszer domború (,,bikonvex'') üveglencsére eső párhuzamos sugárnyaláb ugyancsak párhuzamos nyalábként hagyja el a lencsét? (5 pont)

Közli: Radnai Gyula, Budapest

P. 3508.Egy \(\displaystyle lambda\) hullámhosszúságú foton ütközik egy nyugvónak és szabadnak tekinthető elektronnal. A kölcsönhatás során az elektron meglökődik, s egy 2\(\displaystyle lambda\) hullámhosszúságú foton indul a beesővel ellentétes irányba. Határozzuk meg a beeső foton hullámhosszát! (5 pont)

Közli: Szegedi Ervin, Debrecen

Nagy László verseny, Kazincbarcika

A fizika feladatok megoldásai a következő címekre küldhetők:

KöMaL Szerkesztőség
Budapest 112, Pf. 32.  1518

megoldas@komal.elte.hu (Az interneten keresztül történő beküldésről olvassa el tájékoztatónkat)

A beküldési határidő: 2002. március 11.

Olimpiai levelezés A feladat vázlatos megoldása vagy végeredménye 1 hónapon belül elektronikus (esetleg hagyományos) levélben küldhető be a gnadig@komal.elte.hu címre (illetve a Szerkesztőségbe). Minden levélíró néhány napon belül névre szóló választ kap, melyből megtudhatja, hogy jó-e a megoldása, vagy ha nem, hol hibázott és hogyan léphetne tovább.

OLI. 6. Egy m tömegű álló részecskének M tömegű, a fénysebességgel összemérhető sebességgel mozgó részecske ütközik. Legfeljebb mekkora szögben szóródhat a M tömegű részecske?