 |
Exercises and problems in Informatics |
Please read The Conditions of the Problem Solving Competition.
I. 16. The reciprocal of a number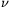 
can be approximated
by Newton's method: from an initial approximation x0
one forms the sequence
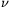xn+1=2xn-.xn2. In order
to achieve very high precision, one can not work with the usual types
of numbers used by programming languages--operations on these numbers
should be devised by us instead.
Write a program (I16.pas,...) which reads a real number (having at
most 100 digits in its integer part and at most 100 digits in its
fractional part), then gives an approximation of its reciprocal
(xn) such that |
xn-xn+1|<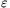
with
a given \(\displaystyle varepsilon\)>0 holds. (10 points)
I. 17. A hubcap is attached onto the wheel of a locomotive engine running on the rail. Radii of the wheel (K) and the hubcap (D), further the velocity of the engine (V) are known. We fix a point on the rim of the hubcap, which is rotated (clockwise) by an angle ALPHA relative to the point on the rail.Using the quantities K, D, V and ALPHA, your program (I17.pas) should draw the trace of a point on the rim of the hubcap.
The first figure shows the case when the two radii are the same, and the point on the rim just touches the ground.
The second figure shows a trace when the radius of the hubcap is 1.5 times of the radius of the wheel, and the wheel in its initial position is already rotated (in the direction of motion) by an angle of 90 degrees. (10 points)
Figure 1
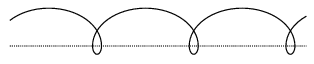
Figure 2
I. 18. In the interrelation of a predator and a prey population, variation of the number of individuals in both populations can be determined by
(the actual number of individuals in the
population).
.(individual birth rate -
individual death rate).
The individual birth rate of predators depends on the available food, that is on the number of the prey population. The death rate of the prey population in turn is proportional to the number of predators.
Prepare a sheet (I18.xls) which computes the number of predators and preys in N steps (2\(\displaystyle le\)N\(\displaystyle le\)60), and graphs them first as functions of time, then in a graph with the number of predators plotted against the number of preys.
Example. Also present some values of the parameters (saved in the file I18.doc) when the number of individuals in both populations remains constant during the simulation. (10 points)