Solutions for exercises "C" in March, 2002

In this page only the sketch of the solutions are published; in some cases only the final results. To achieve the maximum score in the competition more detailed solutions needed.

C. 665. Evaluate the following fraction, given that the numerator and the denominator contain the same number of digits:

\(\displaystyle {166\dots6\over66\dots64}\)

Solution. Let n denote the total number of the digits of 6 in the numerator and denominator. Then

\(\displaystyle \overline{166\ldots6}=10^n+6(1+10+\ldots+10^{n-1})=10^n+6\cdot{{10^n-1}\over{10-1}}=\)

\(\displaystyle =10^n+{{2}\over{3}}(10^n-1)={{5}\over{3}}10^n-{{2}\over{3}}.\)

Similarly,

\(\displaystyle \overline{66\ldots64}=60(1+10+\ldots+10^{n-1})+4=60{{10^n-1}\over{9}}+4=\)

\(\displaystyle ={{20}\over{3}}10^n-{{8}\over{3}}=4\left({{5}\over{3}}10^n-{{2}\over{3}}\right),\)

and thus the value of the fraction is \(\displaystyle {{1}\over{4}}\), independently of the value of n.

C. 666. The value of a quadratic function of integer coefficients is divisible by 3 at every integer. Prove that all three coefficients are divisible by 3.

Solution. Let the polynomial in question be f=ax²+bx+c, where a, b and c are integers. Then 3|f(0)=c according to the condition, and thus the values of f-c=ax²+bx are also divisible by 3. Hence its values a+b and a-b at the points 1 and -1 are also divisible by 3. Terefore, 3|(a+b)+(a-b)=2a and 3|(a+b)-(a-b)=2b, and the statement of the problem immediately follows.

C. 667. Let \(\displaystyle a=x+{1\over x}\), 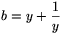, \(\displaystyle c=xy+{1\over xy}\). Prove that the value of the expression a²+b²+c²-abc is independent of x and y.

Solution.

\(\displaystyle a^2=\Big(x+\frac{1}{x}\Big)^2=x^2+{{1}\over{x^2}}+2,\)

\(\displaystyle b^2=\Big(y+\frac{1}{y}\Big)^2=y^2+{{1}\over{y^2}}+2,\)

\(\displaystyle c^2=\Big(xy+\frac{1}{xy}\Big)^2=x^2y^2+{{1}\over{x^2y^2}}+2,\)

and

\(\displaystyle ab=\Big(x+{1\over x}\Big)\Big(y+{1\over y}\Big)=\Big(xy+{1\over xy}\Big)+\Big({x\over y}+{y\over x}\Big)=c+\Big({x\over y}+{y\over x}\Big).\)

Thus

\(\displaystyle abc=c^2+\Big({x\over y}+{y\over x}\Big)c=x^2y^2+{1\over x^2y^2}+2+\Big({x\over y}+{y\over x}\Big)\Big(xy+{1\over xy}\Big)=\)

\(\displaystyle =x^2y^2+{1\over x^2y^2}+2+\Big(x^2+y^2+{1\over x^2}+{1\over y^2}\Big)=a^2+b^2+c^2-4.\)

Therefore a²+b²+c²-abc=4, which is independent of the values of x and y.

C. 668. Given the triangle ABC, find the locus of the points P in the plane of the triangle, such that PA²=PB²+PC².

Solution. Let A^* denote the reflection of point A in the line BC. If the side of the triangle is chosen to be unity then \(\displaystyle \overline{AA^*}=\sqrt{3}\)

; legyen \(\displaystyle \overline{PA^*}=x\). By applying the cosine rule to the triangles PA^*A, PA^*B, PA^*C, we have

\(\displaystyle \overline{PA}^2=\overline{PA^*}^2+\overline{AA^*}^2-2\overline{PA^*}\cdot\overline{AA^*}\cos PA^*A\angle=x^2+3-2x\sqrt{3}\cos PA^*A\angle,\)

\(\displaystyle \overline{PB}^2=\overline{PA^*}^2+\overline{A^*B}^2-2\overline{PA^*}\cdot\overline{A^*B}\cos PA^*B\angle=x^2+1-2x\cos PA^*B\angle,\)

\(\displaystyle \overline{PC}^2=\overline{PA^*}^2+\overline{A^*C}^2-2\overline{PA^*}\cdot\overline{A^*C}\cos PA^*C\angle=x^2+1-2x\cos PA^*C\angle.\)

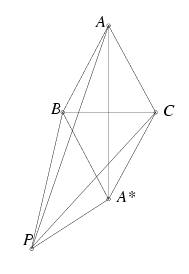
Observe that the difference of the angles PA^*C and PA^*B is BA^*C\(\displaystyle angle\)=60^o, and the arithmetic mean of the two angles is the angle PA^*A, as AA^* bisects the angle BA^*C. By subtracting the first inequality from the sum of the second and third inequalities, and applying the identity

\(\displaystyle \cos\alpha+\cos\beta=2\cos\frac{\alpha+\beta}{2}\cos\frac{\alpha-\beta}{2}\)

, we get

\(\displaystyle \overline{PB}^2+\overline{PC}^2-\overline{PA}^2=2x^2+2-(x^2+3)-2x(\cos PA^*B\angle+\cos PA^*C\angle-\sqrt{3}\cos PA^*A\angle)=\)

\(\displaystyle =x^2-1-2x(2\cos\frac{PA^*B\angle+PA^*C\angle}{2}\cos\frac{PA^*B\angle-PA^*C\angle}{2}-\sqrt{3}\cos PA^*A\angle)=\)

\(\displaystyle =x^2-1-2x(2\cos PA^*A\angle\cdot\cos30^{\circ}-\sqrt{3}\cos PA^*A\angle)=\)

\(\displaystyle =x^2-1-2x\cos PA^*A\angle\cdot(2\frac{\sqrt{3}}{2}-\sqrt{3})=x^2-1.\)

Thus the condition is satisfied by those points P for which \(\displaystyle \overline{PA^*}=x=1\), that is, the points lying on the unit circle centred at A^*.

C. 669. Among all circular sectors with a given perimeter, which one has the greatest area?

Solution. Let r denote the radius of the sectors investigated, let \(\displaystyle alpha\) denote the (radian) measure of their angle, and let K be the given perimeter. Then K=2r+r\(\displaystyle alpha\)=r(2+\(\displaystyle alpha\)), and the double of the area of the sector is 2t=r²\(\displaystyle alpha\). Thus

\(\displaystyle 2t=r^2\Big(\frac{K}{r}-2\Big),\) and hence \(\displaystyle r=\frac{K\pm\sqrt{K^2-16t}}{4}\).

As the discriminant cannot be negative, t can be at most \(\displaystyle \frac{K^2}{16}\), and that value occurs when \(\displaystyle r=\frac{K}{4}\). In that case, \(\displaystyle K=r(2+\alpha)=\frac{K}{4}(2+\alpha)\)

, and thus \(\displaystyle alpha\)=2, ami \(\displaystyle 360\cdot\frac{2}{2\pi}\approx114,59^{\circ}\).