Fizikából kitűzött gyakorlatok és feladatok
2002. március

Kérjük, olvassa el a versenykiírást.

Helyesbítés

A 2001. évi decemberi számban kitűzött P. 3486. feladat hibás adatokat tartalmazott. Az alábbiakban ismételten kitűzött feladat megoldása a mostaniakkal együtt beküldhető, és a decemberi feladatokkal együtt kerül értékelésre.

P. 3486. A ¹⁴N mag kötési energiája 16,76 pJ, a ¹⁴C mag kötési energiája 16,86 pJ.

a) Melyik atommag bomlik a másikra, és miért?

b) Mennyi lehet a bomlás során keletkező töltött részecske mozgási energiája? (5 pont)

A Szilárd Leó nukleáris verseny feladata nyomán

Mérési feladat

M. 232. Függesszünk fel szimmetrikusan egy homogén fémrudat két erős fonállal az ábrán látható módon! Hogyan függ a kicsit megcsavart rendszer periódusideje az l és a b távolságoktól?

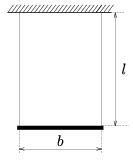
(6 pont)

Közli: Varga István, Békéscsaba

Az elméleti versenyben kitűzött gyakorlatok és feladatok Az elméleti fizika feladatokra kapható pontszám a feladatok nehézségétől függ. Az 1-8. osztályosok versenyében minden hónapban a 3 legnagyobb, a 9-12. osztályosok versenyeiben minden hónapban az 5 legnagyobb pontszám számít be a pontversenybe.

P. 3509. Lehetséges-e, hogy egy elejtett, szabadon eső test az esés utolsó másodpercében kétszer akkora utat tegyen meg, mint az ezt megelőző másodpercben? (3 pont)

Közli: Sütt Dezső, Budapest

P. 3510. Egy 4 dm² alapterületű, függőleges hengerben 32 g tömegű, 0 ^oC hőmérsékletű oxigéngázt 150 kg tömegű dugattyú zár el. A külső légnyomás 1,01^.10⁵ Pa. A henger tengelye függőleges, a dugattyú súrlódás nélkül mozoghat benne.

Milyen magasan áll a dugattyú? Mennyi hőt kell közölni a gázzal, hogy a dugattyú 20 cm-rel feljebb emelkedjék? (4 pont)

Bay Zoltán verseny, Sarkad

P. 3511. Függőleges falba vert szögön lóg egy l hosszú fonálinga. Az ingát vízszintesen kitérítve tartjuk, majd elengedjük. Amikor már a vízszinteshez képest szöggel elfordult, a fonál egy másik szögbe ütközik, s ettől kezdve a fonál végén lévő kis test már e második szög körüli köríven folytatja útját. Milyen messze lehet a második szög az elsőtől, ha a test az új körpályán teljesen végigfut? (4 pont)

Közli: Farkas László, Keszthely

P. 3512. Egy épület egyik oldalát erős napsugárzás éri. Milyen irányú huzat fúj át az épületen, ha a napos és az árnyékos oldalán is kinyitunk egy-egy ablakot? (3 pont)

,,Keresd a megoldást!'' verseny, Szeged

P. 3513. Becsüljük meg, hogy mekkora menetellenállást jelent az autók számára az eső szélcsendben! Tegyük fel, hogy  óra alatt 10 mm csapadék esett, az esőcseppek átmérője 2 mm, az autó homlokfelülete 1,5 m², sebessége 90 km/h. Hogyan aránylik egymáshoz az eső és a levegő sűrűsége? (5 pont)

Közli: Sári Péter, Budapest

P. 3514. \(\displaystyle alpha\)=30^o hajlásszögű, két különböző felülettel rendelkező, hosszú lejtő tetejéről kezdősebesség nélkül induló m=4 kg tömegű, tömör henger mozgását vizsgáljuk. A lejtő első szakasza nagyon sima, a súrlódási tényező \(\displaystyle mu\)₁=0, a második szakaszon pedig a súrlódási tényező \(\displaystyle \mu_2=\mathop{\rm tg}\alpha\). Erre a felületre a henger akkor érkezik, amikor a lejtőn haladva függőleges irányban már h=1,8 m-t süllyedt.

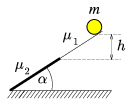
a) Az indítástól számítva mennyi idő múlva fog a henger tisztán gördülni?

b) Mennyi mechanikai energia vész el a henger mozgása során? (5 pont)

Közli: Kotek László, Pécs

P. 3515. Síkkondenzátor egy-egy lemezének területe 1500 cm², a lemezek távolsága 20 mm. Rákapcsoltunk egy 250 V-os telepet, majd betoltunk a lemezek közé, azokkal párhuzamosan egy 5 mm vastag fémlemezt és egy ugyancsak 5 mm vastag üveglemezt (_rel=5). Mennyi munkát végeztünk a lemezek betolása során? (5 pont)

Zemplén Győző verseny, Nagykanizsa

P. 3516. Az ábrán látható négyzetes keresztmetszetű gyűrű egyik fele rézből, másik fele alumíniumból készült. A gyűrű belső sugara 8 cm, külső sugara 10 cm, és bemerül egy, a síkjára merőleges, 0,1 T indukciójú homogén mágneses térbe.

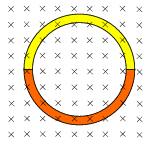
Mekkora töltés halmozódik fel az összeillesztéseknél, ha a mágneses indukció értékét 2 másodperc alatt egyenletesen zérusra csökkentjük? (6 pont)

Közli: Pálfalvi László, Pécs

P. 3517. Egy radioaktív sugárforrás felezési ideje T, s kezdetben r₀ távolságra van a mérőműszerünktől. Egyszer csak elindul felénk úgy, hogy mérőműszerünkön a beütésszám nem változik.

Adjuk meg a sugárforrás és a műszer közötti távolságot az idő függvényében! Mekkora volt a radioaktív forrás kezdősebessége? (A levegő abszorpciós hatásától tekintsünk el!) (5 pont)

Közli: Simon Péter, Pécs

P. 3518. A XIX. században a Napot égő széntömbnek vélték, amely sugárzása által veszíti el energiáját. A napsugárzás intenzitása a Földön 1400 W/m². Tételezzük fel, hogy ez az intenzitás a jövőben sem csökken! A Nap tömege 2^.10³⁰ kg, távolsága a Földtől 1,5^.10¹¹ m, a szén fűtőértéke 30 MJ/kg.

Mennyi ideig sütne még a Nap, ha valóban égő szénből állna? (A számítás eredménye a korabeli tudósokat is meglepte.) (4 pont)

Közli: Korpássy Péter, Budapest

P. 3519. Az ábra szerinti összeállításban az alsó henger dugattyúja kezdetben 10 cm magasan áll, alatta 20 ^oC-os nitrogén, felette higany, amely kitölti a gumicsövet, és a felső edényben van a szabad felszíne, 2 méterrel a dugattyú felett. A henger alapterülete 100 cm², a dugattyú súlytalan, és a nitrogén 30 cm magasságig tágulhat. A külső légnyomás 10⁵ Pa.

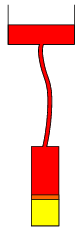
A nitrogént melegítjük, és miközben a dugattyú emelkedik, a felső edényt folyamatosan süllyesztjük oly módon, hogy amíg a dugattyú 1 mm-t emelkedik, azalatt a higany felső szintje 9 mm-rel kerüljön lejjebb. Ezt addig folytatjuk, amíg a nitrogén hőt vesz fel.

Mennyi a felvett hő? Mekkora a nitrogén legnagyobb hőmérséklete? (6 pont)

Közli: Légrádi Imre, Sopron

A fizika feladatok megoldásai a következő címekre küldhetők:

KöMaL Szerkesztőség
Budapest 112, Pf. 32.  1518

megoldas@komal.elte.hu (Az interneten keresztül történő beküldésről olvassa el tájékoztatónkat)

A beküldési határidő: 2002. április 11.

Olimpiai levelezés A feladat vázlatos megoldása vagy végeredménye 1 hónapon belül elektronikus (esetleg hagyományos) levélben küldhető be a gnadig@komal.elte.hu címre (illetve a Szerkesztőségbe). Minden levélíró néhány napon belül névre szóló választ kap, melyből megtudhatja, hogy jó-e a megoldása, vagy ha nem, hol hibázott és hogyan léphetne tovább.

OLI. 7. n₁ és n₂ törésmutatójú közegek határfelülete forgásfelület. Az egyik oldalról (a szimmetriatengellyel párhuzamosan) fénysugarak érkeznek a határfelületre. Milyen alakú legyen a határfelület, ha azt szeretnénk elérni, hogy valamennyi megtört fénysugár a tengelynek a határfelülettől f távolságban lévő pontján haladjon át?

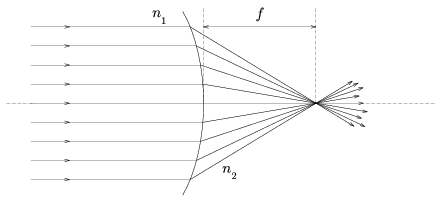
A feladat vázlatos megoldása vagy végeredménye 1 hónapon belül elektronikus (esetleg hagyományos) levélben küldhető be a gnadig@komal.elte.hu címre (illetve a Szerkesztőségbe). Minden levélíró néhány napon belül névre szóló választ kap, melyből megtudhatja, hogy jó-e a megoldása, vagy ha nem, hol hibázott és hogyan léphetne tovább.