New exercises and problems in Mathematics
March 2002

Please read The Conditions of the Problem Solving Competition.

New exercises in March 2002

Maximum score for each exercise (sign "C") is 5 points.

C. 665. Evaluate the following fraction, given that the numerator and the denominator contain the same number of digits:

$\displaystyle {166\dots6\over66\dots64}$

C. 666. The value of a quadratic function of integer coefficients is divisible by 3 at every integer. Prove that all three coefficients are divisible by 3.

C. 667. Let $\displaystyle a=x+{1\over x}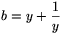$, $b=y+{1\over y}$ , $\displaystyle c=xy+{1\over xy}$. Prove that the value of the expression a²+b²+c²-abc is independent of x and y.

C. 668. Given the triangle ABC, find the locus of the points P in the plane of the triangle, such that PA²=PB²+PC².

C. 669. Among all circular sectors with a given perimeter, which one has the greatest area?

New problems in March 2002

The maximum scores for problems (sign "B") depend on the difficulty. It is allowed to send solutions for any number of problems, but your score will be computed from the 6 largest score in each month.

B. 3532. A bug is crawling about on a sheet of squared paper. In every step, it can move two units to the right, four units to the left, three units up, or five units down the page. During its walk, it makes a turn of exactly 90^o after each step. Which are the fields that the bug can visit in this way? (3 points)

B. 3533. Ann wrote 32 integers on a large sheet of paper, and covered each number with a card. Then he told Bob that if he chose 7 cards, she would tell him whether the sum of the 7 covered numbers is odd or even. At least how many times did Bob have to choose 7 cards in order to find out if the sum of all 32 numbers on the sheet was odd or even? (4 points)

B. 3534. Charging at the opponent's goal, a soccer player has run along a polygonal line not intersecting more than once any straight line parallel to a side of the soccer field. Show that the soccer player cannot have run more than the sum of the two sides of the field. (3 points)

B. 3535. Let U, V, W be points on the lines containing the sides BC, CA and AB of a triangle ABC, respectively. Prove that the perpendiculars drawn to the sides at U, V, and W are concurrent if and only if

AW²+BU²+CV²=AV²+CU²+BW².

(3 points)

B. 3536. Find the minimum value of 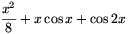${x^2\over8}+x\cos x+\cos2x$ . (4 points)

B. 3537. The foot of the altitude from vertex B of a triangle ABC on side AC is H, the foot of the angle bisector from B is D, and the inscribed circle touches AC at E. The midpoint of the segment AC is F. Prove that EF is the geometric mean of FD and FH. (4 points)

B. 3538. Find a positive real number that will increase by a factor of 2501 if the first and fifth digits after the decimal point are interchanged. (5 points)

B. 3539. There are 8 breakable objects in a box. One of them is worth 50,000 forints (HUF), three are worth 30,000 forints each, and the remaining four are worth 20,000 each. The box is accidentally dropped during transportation. If each object will break with a probability of 1/2 independently of each other, what is the probability that the damage is no more than 100,000 forints? (4 points)

B. 3540. In a triangle, consider the sum of the squares of the heights and the sum of the squares of the sides. In what interval does the ratio of the two numbers vary? (5 points) (based on the idea of Balogh János, Kaposvár)

B. 3541. Let $\displaystyle f(x)={ax+b\over cx+d}$. Prove that if f(f(f(1)))=1, and f(f(f(2)))=3, then f(1)=1. (5 points)

New advanced problems in March 2002

Maximum score for each advanced problem (sign "A") is 5 points.

A. 287. Someone has drawn an ellipse on a sheet of paper, and he has also marked the endpoints of its axes. The major axis is twice as long as the minor axis. Find a construction method for dividing any given acute angle into three equal parts, using a pair of compasses, a straight edge, and the given ellipse only.

A. 288. Let p be an n degree polynomial, where n$\displaystyle ge$1. Prove that there exist at least n+1 complex numbers yielding 0 or 1 as the value of f. (IMC 7, London, 2000)

A. 289. Prove that if the function f is defined on the set of positive real numbers, its values are real, and f satisfies the equation

$\displaystyle f\left({x+y\over2}\right)+f\left({2xy\over x+y}\right)=f(x)+f(y)$

for all positive x,y, then

$\displaystyle 2f\big(\sqrt{xy}\big)=f(x)+f(y)$

for every positive number pair x, y. (Miklós Schweitzer Memorial Competition, 2001)

Send your solutions to the following address:

or by e-mail to:

solutions@komal.elte.hu

Already signed up?
New to KöMaL?