 |
Exercises and problems in Informatics |
Please read The Conditions of the Problem Solving Competition.
I. 19. Fermat's little theorem asserts that if p is a prime and a is an integer not divisible by p, then ap-1-1 is divisible by p, that is
ap-1\(\displaystyle equiv\)1 (mod p).
For example, 212=4096 divided by 13 gives 1 as remainder.
However, the converse of Fermat's little theorem is false, that is if ap-1 is divisible by p, then p is not necessarily a prime number. For example, 2340\(\displaystyle equiv\)1 (mod 341), but 341=11.31. Moreover, there exist composite numbers p which satisfy Fermat's little theorem for every number a<p, being relatively prime to p. These p's are named -- after their discoverer -- Carmichael numbers. The smallest such number is 561.
Write a program (I19.PAS,...) which reads two natural numbers
(1\(\displaystyle le\)N M
M 100 000), then prints
all Carmichael numbers between N and M. (10
points)
100 000), then prints
all Carmichael numbers between N and M. (10
points)
I. 20. A sphere can be represented on the screen by colouring the side being closer to us brighter than its farther parts. Brightness is proportional to the cosine of the angle of incidence of the light, and can be realized using point-cloud representation: white points are placed on the black background very densely at the brightest areas, and the dimmer a part is, the fewer points it gets. Figure 1 shows the sphere illuminated by a parallel beam of light emanating from our viewpoint. The beam on Figure 2 has been rotated around the y-axis by 60 degrees relative to the axis of view. Write a program (I20.PAS,...) which reads the angle between the beam of light and the point of view, then displays the illuminated sphere using point-cloud representation with a red circle placed on the boundary. (10 points)
I. 21. Happy numbers are natural numbers with the
following property: summing the squares of their digits over and over
until the result becomes a one-digit number, we eventually reach the
number 1 itself. For example, 23 is a happy number, since
22+32=13, 12+32=10,
12+02=1. Some other happy numbers include, e.g.,
1 (because 12=1), 7 (because 72=49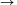 97
97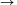 130
130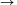 10
10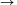 1), 10 (because
12+02=1), or 13 (because
12+32=10\(\displaystyle to\)1).
1), 10 (because
12+02=1), or 13 (because
12+32=10\(\displaystyle to\)1).
|
Prepare a sheet (I21.XLS) which displays whether a given number N is a happy number. The first 3 rows of your sheet should look similar to the example given below. After the value of N has been entered into cell B1, the result should appear in cells B2 and B3 upon simultaneously pressing the keys CTRL and M. (10 points)
