 |
A 2002. áprilisi számban kitűzött fizika elméleti feladatok megoldása |
A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.
P. 3520. Két egymás melletti pályán közlekedő vonat egyike 90 km-t tesz meg óránként, a másik 10 métert másodpercenként. Az egyik vonatban ülő utas azt észleli, hogy a másik vonat 8 másodperc alatt halad el mellette. Milyen hosszú a másik vonat? (3 pont)
Jedlik Ányos megyei verseny, Nyíregyháza
Megoldás. Az egyik vonat sebessége 25 m/s, a másiké 10 m/s, így a relatív sebességük 35 m/s (ha ellentétes irányban haladnak), vagy 15 m/s (ha azonos irányban haladnak). Ezek szerint a másik vonat hossza vagy 280 m, vagy pedig 120 m.
P. 3521. Egy 1,01 dm élhosszúságú üres kockába 10 cm3 vizet öntünk, ezután 1 dm3-es, 0,7 kg tömegű tölgyfakockát teszünk bele. Úszik-e ez a kocka a vízen? (4 pont)
Közli: Pusztai Katalin, Budapest
Megoldás. A fakocka akkor úszik, ha legalább 7 cm mélyen a vízbe merül. Az üres kocka alapterülete 102,01 cm2, ez kb. 2 cm2-rel nagyobb, mint a fakocka alapterülete. Az úszáshoz tehát legalább 2 cm2.7 cm=14 cm3 vízre lenne szükség, így a fakocka nem fog úszni.
P. 3522. Nagyméretű, vízzel nem teljesen teli kád szélére csuklósan rögzítjük egy 0,8 m hosszú, 5 kg/dm3 sűrűségű homogén pálca egyik végét. Ha a pálca másik végére egy 0,4 kg/dm3 sűrűségű, 650 cm3 térfogatú gömböt erősítünk, akkor a gömb elmerül a vízben, s a pálca háromnegyed része is a víz alá merül.
a) Mekkora a pálca keresztmetszete?
b) Mekkora és milyen irányú erőt fejt ki a kád szélénél levő csukló a pálcára? (4 pont)
Közli: Molnár Miklós, Szeged
Megoldás. a) A gömb sugara a térfogatából számítható: r=5,37 cm. A gömbre és a pálca vízbe merülő részére ható felhajtóerőknek a csuklóra vonatkoztatott eredő forgatónyomatéka ugyanakkora kell legyen, mint a gömb, illetve a pálca súlyának megfelelő forgatónyomatékok összege. Innen a pálca keresztmetszetére 2,56 cm2 adódik.
b) A csukló által kifejtett erő (az összes erő egyensúlyának feltételéből) 4,7 N nagyságú, és függőlegesen felfelé mutat.
P. 3523. Az ábra egy pontszerű test sebességét és gyorsulását mutatja a mozgás kezdőpillanatában. A test gyorsulásának iránya és nagysága állandó.

b) Mikor lesz a sebessége minimális?
c) Mekkora a test pályájának minimális görbületi sugara?
(Adatok: a=6 m/s2, v0=24 m/s, \(\displaystyle varphi\)=120o.) (5 pont)
Közli: Holics László, Budapest
Megoldás. a) 4 s.
b) 2 s múlva (vmin=20,78 m/s).
c) Rmin=vmin2/a=72 m.
P. 3524. A kompresszoros hűtőgépben és fűtőgépben (hőszivattyúban) a zárt csőrendszerben áramló közeg (ammónia, freon) ciklusonként ugyanazt a termodinamikai körfolyamatot járja végig. Mitől függ hát, hogy a gép hűtő- vagy fűtőgépként működik? (4 pont)
Közli: Radnai Gyula, Budapest
Megoldás. A hűtőgépnél is és a hőszivattyúnál is alacsonyabb hőmérsékletű testtől hőt vonunk el, magasabb hőmérsékletű testet pedig melegítünk. Ha a melegebb test (a környezet) hőkapacitása sokkal nagyobb, mint a hidegebbé, akkor csak a hidegebb test hőmérséklete változik számottevően, ez a hűtőgép esete. Ha viszont a hidegebb test hőkapacitása sokkal nagyobb, mint a másik testé, akkor csak a melegebb test hőmérséklete változik számottevően: ez a hőszivattyú.
P. 3525. Egy U feszültségre feltöltött síkkondenzátor függőleges, nagyméretű lemezei d távolságra vannak egymástól. A negatív lemezről kezdősebesség nélkül leválik egy Q töltésű, m tömegű részecske. Mekkora sebességgel csapódik ez a negatív részecske a pozitív lemeznek? Mekkora U feszültség esetén minimális ez a sebesség? (5 pont)
Közli: Varga István, Békéscsaba
Megoldás. A részecske negatív töltésű kell legyen (különben nem juthatna el a pozitív lemezhez), tehát Q<0.
A részecske vízszintes irányban egyenletesen gyorsul, gyorsulása
\(\displaystyle \frac{\vert Q\vert\,U}{md}.\)
A vízszintes irányú mozgás végsebessége
\(\displaystyle v_1=\sqrt{\frac{2\vert Q\vert U}{m}},\)
a mozgás ideje pedig
\(\displaystyle t=\sqrt{\frac{2md^2}{\vert Q\vert U}}.\)
Ennyi idő alatt függőlegesen lefelé g gyorsulással
\(\displaystyle v_2=g\sqrt{\frac{2md^2}{\vert Q\vert U}}\)
függőleges sebességre tesz. A teljes végsebesség nagyságának négyzete
\(\displaystyle v^2=v_1^2+v_2^2=\frac{2\vert Q\vert U}{m}+\frac{2md^2g^2}{\vert Q\vert U}.\)
Ez a kifejezés két olyan tag összege, melyek szorzata nem függ U-tól. Felhasználva a számtani és mértani közepekre vonatkozó egyenlőtlenséget v2 (és vele együtt v) akkor minimális, ha
\(\displaystyle U=\frac{mgd}{\vert Q\vert},\)
és ekkor \(\displaystyle v=v_{\rm min}=2\sqrt{gd}.\)
P. 3526. Mindkét végén derék- szögben meghajlított, vékony, elektromosan szigetelő cső végein r, illetve R sugarú szappanbuborék van. Mekkora elektromos töltést adjunk az egyik buboréknak, hogy a másik buborék mérete a cső közepén levő csap kinyitása után ne változzék meg? (Az elektromos megosztástól tekintsünk el!) (5 pont)
Közli: Pálfalvi László, Pécs
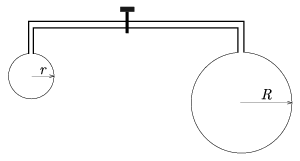
Megoldás.
\(\displaystyle Q=\sqrt{\frac{32\pi\alpha}{k}\cdot r^3\cdot\frac{p_0+\frac{4\alpha}{r}}{p_0+\frac{4\alpha}{R}} \cdot\left(1-\frac{r}{R}\root3\of{\frac{p_0+\frac{4\alpha}{r}} {p_0+\frac{4\alpha}{R}}}\,\right)}. \)
Mivel reális méretű buborékoknál \(\displaystyle p_0\gg\frac{4\alpha}{r}\), jó közelítéssel fennáll
\(\displaystyle Q\approx\sqrt{\frac{32\pi\alpha}{k}\cdot r^3 \cdot\left(1-\frac{r}{R}\right)}.\)
P. 3527. Függőleges, igen hosszú, rövidre zárt tekercsbe az ábrán látható módon mágnesrudat ejtünk. Ábrázoljuk vázlatosan a tekercsben folyó áramot és a mágnesrúd gyorsulását az idő függvényében! (5 pont)
Közli: Kovács Gyula, Gyömrő
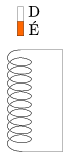
Megoldás. A mágnesre a nehézségi erő és a szolenoid mágneses tere hat. Ez utóbbi hatás a mágnesen kívül és mágnes belsejében egyaránt elhanyagolható, hiszen homogén mágneses mező egy mágneses dipólusra csak forgatónyomatékot fejt ki, erőt nem. Számottevő erőhatást (erőlökést) csak a szolenoid végeinél várhatunk. Az erőlökés nagysága a tekercsben folyó áramerősséggel arányos, iránya pedig (adott áramerősség esetén) a tekercs alján és tetején ellentétes.
A tekercsben folyó áram időbeli változását az indukált feszültség és a tekercs ohmos ellenállásán eső feszültség egyenlősége határozza meg. A teljes indukált feszültség két tag (a tekercs áramának változása által keltett önindukciós feszültség és a mozgó mágnes fluxusának változásával arányos kifejezés) összegeként áll elő.
Kezdetben az áramerősség nulla. Amikor (bizonyos t=t1 időpont környékén) a mágnesrúd eléri a tekercs felső végét, a tekercsben áram indul, a mágnesrúd pedig lelassul, esetleg meg is állhat. Ha elegendően magasról ejtettük a mágnesrudat, az bejut a tekercs belsejébe, s mivel ott már a tekercs mágneses tere nem fejt ki rá eredő erőt, ismét szabadon esik. Eközben a tekercs árama csak az ohmos veszteségek miatt csökken, a tekercs belsejében mozgó mágnesrúd nem indukál feszültséget (hatás - ellenhatás). Ha a tekercs ohmos ellenállása kicsi (pl. ha szupravezető a tekercs), akkor az áramerősség állandó marad mindaddig, míg a mágnesrúd el nem éri a tekercs alsó végét. (Számottevő ohmos ellenállás esetén az áram időben exponenciálisan csökken.) Amikor (bizonyos t=t2 időpont környékén) a mágnesrúd eléri a tekercs alsó végét, a tekercsben olyan irányú feszültséget indukál, ami csökkenteni fogja a korábban kialakult áramot. A tekercs mágneses energiája lecsökken, miközben a mágnesrúd sebessége megnő. Ha a tekercs ohmos ellenállása elhanyagolhatóan kicsi, akkor a mágnesrúd éppen akkora sebességgel fog mozogni a tekercs elhagyása után, mint amekkorával akkor rendelkezne, ha a tekercs ott sem lenne.
Ha a tekercs ohmos ellenállása olyan nagy, hogy a benne megindított áramnak megfelelő mágneses energiát a Joule-hő ,,felemészti'', mire a mágnes a tekercs aljához ér, akkor a feszültséglökés a korábbival ellentétes irányú áramot indít a tekercsben, s ez a mágnest nem gyorsítja, hanem fékezi.
P. 3528. Az ábrán látható optikai rendszerben az n1 és n2 törésmutatójú közegek közös határfelülete R sugarú gömbfelület. Van-e a t tengelyen olyan pont, ahonnan (t-vel kis szögben) kiinduló fénysugarak a másik közegben a tengellyel párhuzamosan haladnak? (5 pont)
Közli: Erdélyi Róbert, Budapest
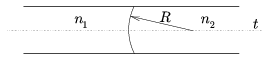
Megoldás. Csak akkor létezik ilyen pont, ha n2>n1, ekkor viszont kettő pont is eleget tesz a kívánt feltételnek: az n1 törésmutatójú közegben a határfelülettől f1=Rn1/(n2-n1) távolságban, illetve az n2 törésmutatójú közegben a határfelülettől f2=Rn2/(n2-n1) távolságban.
P. 3529. A XX. század elején a Napot egy 6000 K hőmérsékletű, homogén izzó gázgömbnek képzelték, amely H2 molekulákból áll, és a hősugárzás során lassan hűl. A napsugárzás intenzitása a Földünk távolságában jelenleg 1400 W/m2.
Becsüljük meg, mennyi idő múlva sötétülne el a Nap, vagyis csökkenne a hőmérséklete kb. 1000 K-re? (Ma már tudjuk, hogy a Nap - hasonlóan a többi csillaghoz - sugárzását atommagok fúziójakor felszabaduló energiából nyeri, és még kb. 5 milliárd évig süt!) (5 pont)
Közli: Korpássy Péter, Budapest
Megoldás. Ha a Nap sugárzásának teljesítménye nem csökkenne, akkor a mai sugárzási intenzitás mellett (és a Nap anyagának fajhőjét az alacsony hőmérsékleten érvényes adattal közelítve) a kihűlés idejére kb. 8000 év adódna. Ha figyelembe vesszük, hogy a sugárzás intenzitása a hőmérséklet csökkenésével (a Stefan-Boltzmann-törvénynek megfelelő módon) csökken, akkor kb. 500 000 évnyi időt kapunk.
P. 3530. Mennyi az ábrán látható végtelen lánc eredő váltóáramú ellenállása \(\displaystyle omega\) körfrekvencián az A-B kapcsok között? Lehet ez kétféle érték? (6 pont)
Közli: Kós Géza, Budapest
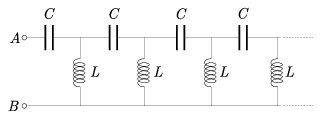
A végtelen lánc eredő impedanciája \(\displaystyle \omega<\frac{1}{2\sqrt{LC}}\) esetben:
\(\displaystyle Z= \frac{1+\sqrt{1-4\omega^2LC}}{2\omega C}.\)
Amennyiben \(\displaystyle \omeg\)\frac{1}{2\sqrt{LC}}">, az n tagú lánc impedanciájának n\(\displaystyle \rightarrow\) esetén nem létezik határértéke, tehát a hosszú (de nem végtelen hosszú!) lánc váltóáramú ellenállása attól függ, hogy ténylegesen milyen hosszú is a ,,nagyon hosszú''.
esetén nem létezik határértéke, tehát a hosszú (de nem végtelen hosszú!) lánc váltóáramú ellenállása attól függ, hogy ténylegesen milyen hosszú is a ,,nagyon hosszú''.

