Fizikából kitűzött gyakorlatok és feladatok
2002. április

Kérjük, olvassa el a versenykiírást.

Mérési feladat

M. 233. Az asztalra fektetett gyufásdobozra tegyünk rá egy vízzel telt, kisméretű poharat. Egy vonalzóval üssük ki a gyufásdobozt a pohár alól. Végezzünk egyszerű méréseket (például mérjük meg a pohár elmozdulását is), s ezek alapján becsüljük meg, mennyi idő alatt ütöttük ki a gyufásdobozt! (6 pont)

Közli: Honyek Gyula, Budapest

Az elméleti versenyben kitűzött gyakorlatok és feladatok

Az elméleti fizika feladatokra kapható pontszám a feladatok nehézségétől függ. Az 1-8. osztályosok versenyében minden hónapban a 3 legnagyobb, a 9-12. osztályosok versenyeiben minden hónapban az 5 legnagyobb pontszám számít be a pontversenybe.

P. 3520. Két egymás melletti pályán közlekedő vonat egyike 90 km-t tesz meg óránként, a másik 10 métert másodpercenként. Az egyik vonatban ülő utas azt észleli, hogy a másik vonat 8 másodperc alatt halad el mellette. Milyen hosszú a másik vonat? (3 pont)

Jedlik Ányos megyei verseny, Nyíregyháza

P. 3521. Egy 1,01 dm élhosszúságú üres kockába 10 cm³ vizet öntünk, ezután 1 dm³-es, 0,7 kg tömegű tölgyfakockát teszünk bele. Úszik-e ez a kocka a vízen? (4 pont)

Közli: Pusztai Katalin, Budapest

P. 3522. Nagyméretű, vízzel nem teljesen teli kád szélére csuklósan rögzítjük egy 0,8 m hosszú, 5 kg/dm³ sűrűségű homogén pálca egyik végét. Ha a pálca másik végére egy 0,4 kg/dm³ sűrűségű, 650 cm³ térfogatú gömböt erősítünk, akkor a gömb elmerül a vízben, s a pálca háromnegyed része is a víz alá merül.

a) Mekkora a pálca keresztmetszete?

b) Mekkora és milyen irányú erőt fejt ki a kád szélénél levő csukló a pálcára? (4 pont)

Közli: Molnár Miklós, Szeged

P. 3523. Az ábra egy pontszerű test sebességét és gyorsulását mutatja a mozgás kezdőpillanatában. A test gyorsulásának iránya és nagysága állandó.

a) Mennyi idő múlva lesz a test sebességének nagysága ugyanakkora, mint a kezdőpillanatban volt?

b) Mikor lesz a sebessége minimális?

c) Mekkora a test pályájának minimális görbületi sugara?

(Adatok: a=6 m/s², v₀=24 m/s, $\displaystyle varphi$=120^o.) (5 pont)

Közli: Holics László, Budapest

P. 3524. A kompresszoros hűtőgépben és fűtőgépben (hőszivattyúban) a zárt csőrendszerben áramló közeg (ammónia, freon) ciklusonként ugyanazt a termodinamikai körfolyamatot járja végig. Mitől függ hát, hogy a gép hűtő- vagy fűtőgépként működik? (4 pont)

Közli: Radnai Gyula, Budapest

P. 3525. Egy U feszültségre feltöltött síkkondenzátor függőleges, nagyméretű lemezei d távolságra vannak egymástól. A negatív lemezről kezdősebesség nélkül leválik egy Q töltésű, m tömegű részecske. Mekkora sebességgel csapódik ez a negatív részecske a pozitív lemeznek? Mekkora U feszültség esetén minimális ez a sebesség? (5 pont)

Közli: Varga István, Békéscsaba

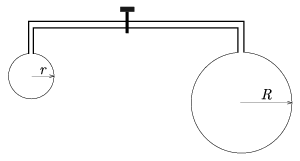
P. 3526. Mindkét végén derék- szögben meghajlított, vékony, elektromosan szigetelő cső végein r, illetve R sugarú szappanbuborék van. Mekkora elektromos töltést adjunk az egyik buboréknak, hogy a másik buborék mérete a cső közepén levő csap kinyitása után ne változzék meg? (Az elektromos megosztástól tekintsünk el!) (5 pont)

Közli: Pálfalvi László, Pécs

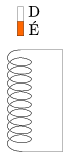
P. 3527. Függőleges, igen hosszú, rövidre zárt tekercsbe az ábrán látható módon mágnesrudat ejtünk. Ábrázoljuk vázlatosan a tekercsben folyó áramot és a mágnesrúd gyorsulását az idő függvényében! (5 pont)

Közli: Kovács Gyula, Gyömrő

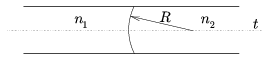
P. 3528. Az ábrán látható optikai rendszerben az n₁ és n₂ törésmutatójú közegek közös határfelülete R sugarú gömbfelület. Van-e a t tengelyen olyan pont, ahonnan (t-vel kis szögben) kiinduló fénysugarak a másik közegben a tengellyel párhuzamosan haladnak? (5 pont)

Közli: Erdélyi Róbert, Budapest

P. 3529. A XX. század elején a Napot egy 6000 K hőmérsékletű, homogén izzó gázgömbnek képzelték, amely H₂ molekulákból áll, és a hősugárzás során lassan hűl. A napsugárzás intenzitása a Földünk távolságában jelenleg 1400 W/m².

Becsüljük meg, mennyi idő múlva sötétülne el a Nap, vagyis csökkenne a hőmérséklete kb. 1000 K-re? (Ma már tudjuk, hogy a Nap - hasonlóan a többi csillaghoz - sugárzását atommagok fúziójakor felszabaduló energiából nyeri, és még kb. 5 milliárd évig süt!) (5 pont)

Közli: Korpássy Péter, Budapest

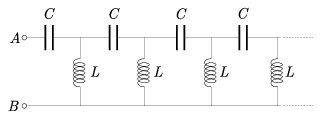
P. 3530. Mennyi az ábrán látható végtelen lánc eredő váltóáramú ellenállása $\displaystyle omega$ körfrekvencián az A-B kapcsok között? Lehet ez kétféle érték? (6 pont)

Közli: Kós Géza, Budapest

A fizika feladatok megoldásai a következő címekre küldhetők:

KöMaL Szerkesztőség

Budapest 112, Pf. 32. 1518

illetve

megoldas@komal.elte.hu

tájékoztatónkat

A beküldési határidő: 2002. május 11.

Olimpiai levelezés

A feladat vázlatos megoldása vagy végeredménye 1 hónapon belül elektronikus (esetleg hagyományos) levélben küldhető be a gnadig@komal.elte.hu címre (illetve a Szerkesztőségbe). Minden levélíró néhány napon belül névre szóló választ kap, melyből megtudhatja, hogy jó-e a megoldása, vagy ha nem, hol hibázott és hogyan léphetne tovább.

OLI. 8. Egy kicsiny tömegű, R sugarú állócsigán L hosszú, m tömegű súlyos, hajlékony kötelet vetünk át (L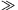 $gg$ R). Kezdetben a kötél áll, és majdnem pontosan szimmetrikusan lóg le a csiga két oldalán. Az instabil helyzetből a kötél kimozdul, és egyre nagyobb gyorsulással mozog. Melyik helyzetében válik el a kötél a csigától?

Áprilisi pótfeladat. (Beküldhető, de az eredménye nem számít bele a pontversenybe.)

Egy vezető napilap 2002. április 1-jei számában jelent meg a következő közlemény:

Egy gumi-multi cég reklámfőnöke úgy akarja vállalata hírnevét az egekig növelni, hogy ajánlatot készül tenni a világ országainak, melyben megoldást kínál a radioaktív hulladékok kezelésére. Az ötlet lényege egy szuper-csúzli, mellyel olyan nagy sebességgel lőhetnék ki 100 kg-os kapszulákban a Földről a hulladékot, hogy azok többet nem térnének vissza. A cég egyik sikeres terméke ugyanis egy olyan gumiszál, amely rugalmas módon hosszának kétszeresére nyújtható méterenként 1000 N erő hatására.

A cég főmérnöke rövid számolás után arra a következtetésre jutott, hogy a vállalat egyik telephelye sem elég nagy a szuper-csúzli felállítására, és javasolja, hogy többszörös gumiszálból álló köteget használjanak. Igaza van-e a főmérnöknek? Hány szálból készüljön a köteg, ha a vállalat legnagyobb rendelkezésre álló területe 6300 méter hosszú? (A számolásban a levegő fékező hatásától és a gumiszál tehetetlenségétől tekintsünk el.) Mekkora gyorsulással indulna a különlegesen erős acélból készült kapszula? Kibírná-e ezt a gyorsulást?

Válaszát küldje a gotoheaven@multigumi.com címre!

Lejegyezte: Honyek Gyula, Budapest

Már regisztráltál?
Új vendég vagy?