Mathematical and Physical Journal
for High Schools
Issued by the MATFUND Foundation
Already signed up?
New to KöMaL?

Exercises and problems in Informatics
April 2002

Please read The Conditions of the Problem Solving Competition.

I. 22. A pack of N cards is placed on the verge of a table in such a way that the upper cards are gradually shifted away from the table to the greatest possible extent such that the pack still keeps its balance.

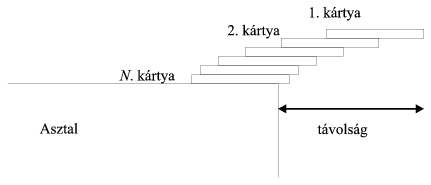
Write a program (I22.PAS) which, for a given number of cards, computes the distance between the right-hand side of the uppermost card and the verge of the table. The cards are assumed to have unit size. (10 points)

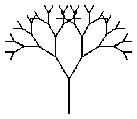
I. 23. We model the growth of a tree as follows. A trunk of length H grows in the first time step, then two branches (with an angle ALPHA between them and of length X times of the trunk) appear symmetrically at the end of the trunk in the next time step. Each of these grows then two new twigs (X times as long as the previous ones) in the subsequent time steps, and so on.

TREE(50,3)TREE(50,6)TREE(75,11)
TREE(75,13)

Your program (I23.PAS, ...) should read the values of H, X, ALPHA (in degrees), and the number of time steps, then draw the corresponding tree. The figures represent trees with X=3/4 and ALFA=60, further H and the number of time steps are (50,3), (50,6), (75,11) and (75,13), respectively. (10 points)

I. 24. The railway line connecting Gotham and Rockwell has 9 stations (together with both terminal stations). Running times between adjacent stations are known. Two trains depart from the terminal stations in the opposite direction. Both trains stay for 1 minute at each station. Since there is only one track between the stations, a train can not depart until the other one coming from the opposite direction has arrived (see page 235). (If they are to depart at the same time, the train from Gotham has priority.)

Prepare your sheet (I24.XLS) which computes the departures and arrivals for each station every time the road times (second row) and departure times from both terminal stations (thick boxes) have been changed. The solution should be given in minutes. (10 points)

Station:
1
2
3
4
5
6
7
8
9
Time:
10
 
10
 
5
 
10
 
10
 
5
 
10
 
8
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
d
a
d
a
d
a
d
a
d
a
d
a
d
a
d
a
From Gotham:
23
33
34
44
45
50
51
61
62
72
73
78
79
89
90
98
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
a
d
a
d
a
d
a
d
a
d
a
d
a
d
a
d
From Rockwell:
99
89
88
78
77
72
71
61
51
41
40
35
34
24
23
15

Send your solutions to the following e-mail address:

Deadline: 13 May 2002