A 2002. májusi B-jelű matematika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

B.3552.Az a₁, a₂, ..., a_2n+1 sorozat minden tagja 2, 5 vagy 9. Tudjuk, hogy a sorozat bármely két szomszédos tagja különböző és a₁=a_2n+1. Bizonyítsuk be, hogy a₁a₂-a₂a₃+a₃a₄-a₄a₅+...-a_2na_2n+1=0. (3 pont)

Megoldás: Ha n=1, akkor a₁a₂-a₂a₃=a₁a₂-a₂a₁=0. Tegyük fel tehát, hogy n>1, és az állítást n-1 esetén már igazoltuk. Ha van olyan 1$\displaystyle le$i$\displaystyle le$2n-1 index, amelyre a_i=a_i+2, akkor hagyjuk el a sorozatból az a_i és a_i+1 elemeket. Az így keletkező b₁,b₂,...b_2n-1 sorozatra ugyanúgy teljesülnek a feltételek, mint az eredeti sorozatra, ezért az indukciós feltevés miatt

S'=b₁b₂-b₂b₃+...-b_2n-2b_2n-1=0 .

Így S=S'+a_ia_i+1-a_i+1a_i+2=0+a_ia_i+1-a_i+1a_i=0, ha i páratlan, és hasonlóképp S=S'-a_ia_i+1+a_i+1a_i+2=0, ha i páros. Ha pedig nincsen olyan i index, amelyre a_i=a_i+2, akkor minden 1$\displaystyle le$i$\displaystyle le$2n-2 indexre a_i+3$\displaystyle ne$a_i+2$\displaystyle ne$a_i és a_i+3$\displaystyle ne$a_i+1$\displaystyle ne$a_i, tehát a_i+3=a_i. Ekkor n szükségképpen osztható 3-mal, valamint a₁=a₄=...=a_2n+1, a₂=a₅=...=a_2n-1 és a₃=a₆=...=a_2n, az n=3k jelöléssel élve tehát

$\displaystyle S=\sum_{i=0}^{k-1}(a_{6i+1}a_{6i+2}-a_{6i+2}a_{6i+3}+\ldots-a_{6i+6}a_{6i+7})=$

$\displaystyle =\sum_{i=0}^{k-1}(a_1a_2-a_2a_3+a_3a_1-a_1a_2+a_2a_3-a_3a_1)=0\ .$

B.3553.Az ABC háromszög A csúcsából induló magasság, B csúcsából induló szögfelező és C csúcsából induló súlyvonal a szemközti oldalakat rendre az A₁, B₁, C₁ pontokban metszi. Bizonyítsuk be, hogy ha az A₁B₁C₁ háromszög szabályos, akkor az ABC háromszög is szabályos. (4 pont)

Megoldás: A BA₁B₁ és BC₁B₁ háromszögekben a BB₁ oldal közös, az egyenlő hosszúságú A₁B₁ és C₁B₁ oldalakkal szemben lévő A₁BB₁ illetve C₁BB₁ szögek pedig megegyeznek. Így két eset képzelhető el: vagy egybevágó a két háromszög, vagy pedig a BA₁B₁ és BC₁B₁ szögek 180^o-ra egészítik ki egymást. A második eset azonban nem lehetséges, ugyanis akkor a BA₁B₁C₁ négyszög húrnégyszög lenne, ahonnan az A₁BC₁ szög nagyságára 120^o adódna, ellentmondásban azzal a feltevéssel, hogy az A-ból induló magasság metszi a BC oldalt, ami megkívánja, hogy az ABC szög hegyesszög legyen.

A BA₁B₁ és BC₁B₁ háromszögek egybevágóságából, valamint abból, hogy a C₁ pont az AB szakasz felezőpontja, következik, hogy az ABA₁ derékszögű háromszögben BA₁=BC₁=C₁A, tehát az ABA₁ szög 60^o-os, a BA₁C₁ háromszög pedig szabályos. Ennélfogva B₁C₁=C₁A₁=BC₁=C₁A, továbbá BC₁A₁$\displaystyle angle$=A₁C₁B₁$\displaystyle angle$=60^o, tehát a B₁C₁A szög is 60^o és így az AC₁B₁ háromszög is szabályos. Az ABC háromszögnek tehát B-nél és A-nál lévő szöge is 60^o, következésképpen az ABC háromszög is szabályos.

B.3554. Az ABCD paralelogramma átlói az M pontban metszik egymást. Az A, M, B pontokon átmenő kör érinti a BC egyenest. Bizonyítsuk be, hogy a B, M, C pontokon átmenő kör érinti a CD egyenest. (3 pont)

Megoldás: Tekintsük az AMB háromszög köré írt kört. Ebben az AMB és CBA szögek egyaránt az AB húrhoz tartozó kerületi szögek, melyek 180^o-ra egészítik ki egymást. Ezért

BMC$\displaystyle angle$+DCB$\displaystyle angle$=(180^o-AMB$\displaystyle angle$)+(180^o-CBA$\displaystyle angle$)=180^o.

Így a BMC háromszög köré írt körben a DCB szög a BC húrhoz tartozó, BMC szöggel szemben fekvő kerületi szög, vagyis a DC egyenes valóban érinti ezt a kört.

B.3555. Egy 2n+1-tagú társaság bármely n-tagú csoportjához van a társaságnak olyan a csoporthoz nem tartozó tagja, aki a csoport minden tagját ismeri. Az ismeretséget kölcsönösnek tételezzük fel. Bizonyítsuk be, hogy a társaságnak van olyan tagja, aki mindenkit ismer. (5 pont)

Megoldás: Tegyük fel, hogy az állítás nem igaz: a társaság minden tagjához talalható olyan tagja a társaságnak, akit az illető nem ismer. Először is azt állítjuk, hogy a társaság tagjait két nem üres csoportba (A és B) lehet osztani úgy, hogy mindenkihez található a másik csoportban olyan ember, akit az illető nem ismer. Valóban, legyen először a és b a társaságnak két olyan tagja, akik nem ismerik egymást, és legyen A₁={a}, B₁={b}. A társaság tagjainak halmazát X-szel jelölve, tegyük fel, hogy A_i és B_i az X két diszjunkt részhalmaza, amelyekre teljesül, hogy minden x$\displaystyle in$A_i esetén van y$\displaystyle in$B_i úgy, hogy x nem ismeri y-t, és minden y$\displaystyle in$B_i esetén van x$\displaystyle in$A_i is úgy, hogy x nem ismeri y-t. Ha A_i$\displaystyle cup$B_i=X, akkor készen vagyunk: az A=A_i, B=B_i választás megfelelő. Ellenkező esetben legyen x_i$\displaystyle in$X$A_i\(\displaystyle cup$B_i), és y_i olyan tagja a társaságnak, aki x_i-t nem ismeri. Ha y_i$\displaystyle in$A_i, akkor legyen A_i+1=A_i és B_i+1=B_i$\displaystyle cup${x_i}. Ha y_i$\displaystyle in$B_i, akkor legyen A_i+1=A_i$\displaystyle cup${x_i} és B_i+1=B_i. Ha pedig $\displaystyle y_i\not\in A_i\cup B_i$, akkor legyen A_i+1=A_i$\displaystyle cup${x_i} és B_i+1=B_i$\displaystyle cup${y_i}. Bármelyik esetben A_i+1 és B_i+1 diszjunkt részhalmazai X-nek amelyekre teljesül, hogy minden x$\displaystyle in$A_i+1 esetén van y$\displaystyle in$B_i+1 úgy, hogy x nem ismeri y-t, és minden y$\displaystyle in$B_i+1 esetén van x$\displaystyle in$A_i+1 is úgy, hogy x nem ismeri y-t. Továbbá A_i$\displaystyle cup$B_i valódi részhalmaza A_i+1$\displaystyle cup$B_i+1-nek. Ezért lesz olyan i$\displaystyle ge$1 index, amelyre A_i$\displaystyle cup$B_i=X, amivel állításunkat igazoltuk.

Az általánosság megszorítása nélkül feltehetjük, hogy |A|$\displaystyle le$|B|, ekkor |A|$\displaystyle le$n. Legyen A' olyan n -elemű részhalmaza X-nek, amely tartalmazza A-t. Ekkor $\displaystyle B'=X\setminus A'\subseteq B$, és ezért B' minden y eleméhez található A-nak (és így A'-nek is) olyan x eleme, hogy x és y nem ismerik egymást. Az A' n-tagú csoporthoz tehát nincs a társaságnak olyan, a csoporthoz nem tartozó tagja, aki a csoport minden tagját ismeri. Ez az ellentmondás mutatja, hogy kiindulási feltevésünk nem lehet helyes, amivel a feladat állítása igazolást nyert.

B.3556. Szerkesszünk háromszöget, ha adott két oldala és a közös csúcsukból induló külső szögfelező. (4 pont)

Megoldás: A szerkeszthetőségnek nyilván szükséges feltétele, hogy a két adott oldal különböző hosszúságú legyen. Tegyük fel, hogy a szerkesztendő ABC háromszögnek a=BC és b=AC oldala adott, ahol a<b. Jelölje a C csúcsból induló belső, illetve külső szögfelező AB egyenessel alkotott metszéspontját F és G, ekkor az A,F,B,G pontok ebben a sorrendben helyezkednek el az AB egyenesen. A szögfelező tétel szerint BF:FA=a:b, így AF=bc/(a+b) és BF=ac/(a+b), ahol c=AB. A C csúcs és az F pont tehát egyaránt az AB szakaszra emelt b:a arányú Apollóniusz-körön helyezkedik el. Mivel az FCG szög derékszög és a G pont illeszkedik ezen kör F-ből induló átmérőjének egyenesére, a G pont éppen a kör AB egyenessel alkotott második metszéspontja. Innen GA:GB=b:a, GA=bc/(b-a), GB=ac/(b-a) következik.

Minthogy a CG=f jelöléssel élve a C csúcs rajta van a GA szakaszhoz tartozó f:b arányú Apollóniusz-körön is, egy, a keresett háromszöghöz hasonló $\displaystyle A'B'C'\triangle$ a következőképpen szerkeszthető meg. Vegyünk fel egy tetszőleges A'B' szakaszt. Erre a b:a arányú k Apollóniusz-kört megszerkesztve, az az A'B' szakaszon kívül egy G' pontban metszi az A'B' egyenest. Ekkor a G'A' szakasz fölé f:b arányban megszerkesztett Apollóniusz-kör k-val alkotott C' metszéspontjára az $\displaystyle A'B'C'\triangle$ hasonló a megszerkesztendő ABC háromszöghöz, melyet egy alkalmas nagyítással már könnyen megszerkeszthetünk.

A szerkeszthetőség feltétele, hogy a két Apollóniusz-kör messe egymást, vagyis hogy a GF:FA arány (f:b)-nél kisebb legyen.

$\displaystyle GF=GB+BF={ac\over b-a}+{ac\over a+b}={2abc\over(b-a)(a+b)}$

miatt ez az f>bGF/FA vagyis f>2ab/(b-a) feltétellel ekvivalens, melynek teljesülése esetén a megoldás egybevágóság erejéig egyértelmű.

B.3557. Kezdődhet-e egy köbszám tízes számrendszerbeli alakja 2002 darab egyessel? (4 pont)

Megoldás: Általánosabban, megmutatjuk, hogy tetszőleges A pozitív egész számhoz található olyan köbszám, melynek tízes számrendszerbeli alakja éppen az A szám tízes számrendszerbeli alakjával kezdődik. Legyen A számjegyeinek száma k, és tekintsük a köbszámokat 1-től 10^3k+3=(10^k+1)³-ig. Két egymást követő ilyen köbszám különbsége alkalmas 1$\displaystyle le$a<10^k+1 egész szám segítségével d=(a+1)³-a³ alakban írható fel, ahol

d=3a²+3a+1<3^.10^2k+2+3^.10^k+1+1<10^2k+3.

Ezért az [1,10^3k+3] intervallumban tetszőleges 10^2k+3 egymást követő egész szám között kell legyen legalább egy eleme az 1³,2³,...,(10^k+1)³ sorozatnak. Mivel A<10^k miatt az

A^.10^2k+3,A^.10^2k+3+1,...,(A+1)^.10^2k+3-1

számok mindegyike az említett intervallumba esik, ezen számok között is kell, hogy legyen legalább egy köbszám, ennek tízes számrendszerbeli alakja pedig éppen az A szám tízes számrendszerbeli alakjával kezdődik.

B.3558. Van-e olyan nem konstans egész együtthatós polinom, amelyik minden pozitív egész helyen 2-hatvány értéket vesz föl? (4 pont)

OKTV 2002 nyomán

Megoldás: Tegyük fel, hogy p(x)=a_nxⁿ+...+a₁x+a₀ ilyen polinom, ahol n$\displaystyle ge$1, a_n$\displaystyle ne$0 és a₀,a₁,...,a_n-1 is egész számok. Legyen M=|a_n|+...+|a₀|, ekkor x$\displaystyle ge$M esetén

$\displaystyle p(x)\le|p(x)|\le\sum_{i=0}^n|a_i|x^i\le\sum_{i=0}^n|a_i|x^n=Mx^n\le x^{n+1}.$

Azt állítjuk, hogy ha x$\displaystyle ge$2^(n+1)², akkor xⁿ⁺¹$\displaystyle le$2^x/(n+1). Ha x-et 2^N alakban írjuk fel, akkor xⁿ⁺¹=2^(n+1)N és 2^x/(n+1)=2^{2^N/(n+1)}, ezért az exponenciális függvény monotonitására hivatkozva elég azt belátni, hogy ha N$\displaystyle ge$(n+1)², akkor (n+1)N$\displaystyle le$2^N/(n+1), vagyis (n+1)²N$\displaystyle le$2^N. Ehhez pedig n$\displaystyle ge$1 miatt elegendő annyit igazolni, hogy ha N$\displaystyle ge$4, akkor N²$\displaystyle le$2^N. Ez következik abból, hogy N=4 esetén N²=2^N, N$\displaystyle ge$4 esetén pedig az f(n)=N² függvény deriváltja, 2N kisebb a g(N)=2^N függvény ln2^.2^N deriváltjánál. Ez utóbbi állítás igazolásához pedig csak annyit kell látni, hogy ln2>1/2 miatt N=4 esetén f'(N)<g'(N), N$\displaystyle ge$4 esetén pedig az f'(N) függvény deriváltja, 2 kisebb a g'(N) függvény deriváltjánál, ami (ln2)²2^N.

Összefoglalva megállapíthatjuk, hogy ha x$\displaystyle ge$M₀=max{M,2^(n+1)²}, akkor p(x)$\displaystyle le$2^x/(n+1). Legyen most T>n(n+1)M₀ egész szám. Mivel a p(x) polinom minden x egész helyen kettőhatvány értéket vesz fel, az M₀,M₀+1,...,T helyeken értéke csakis 2⁰=1,2¹=2,...,2^[T/(n+1)] lehet, vagyis az 1,2,...,T helyeken legfeljebb

$\displaystyle M_0-1+{T\over n+1}+1<{T\over n(n+1)}+{T\over n+1}={T\over n}$

különböző értéket vehet fel. Ez azonban ellentmond annak, hogy a polinom minden értéket legfeljebb n-szer vehet fel. Ilyen polinom tehát nem létezik.

B.3559. Adottak a síkon az e₁, e₂, ..., e_n egyenesek. Az e₁ egyenes egy tetszőleges P₁ pontjából merőlegest bocsátunk az e₂-re, ennek talppontja P₂. Ezután a P₂-ből e₃-ra bocsátott merőleges talppontja P₃, és így tovább, végül az e_n egyenesen kapott P_n pontból az e₁-re bocsátott merőleges talppontja P_n+1. Bizonyítsuk be, hogy az e₁ egyenesnek van olyan P₁ pontja, hogy az így kapott P_n+1 egybeesik P₁-gyel. (4 pont)

Megoldás: Ha az összes egyenes párhuzamos, akkor az állítás nyilvánvaló. Ellenkező esetben tekintsünk egy kört, melynek O középpontja az e₁ egyenesre esik és amely belsejében tartalmazza az egyenesek valamennyi metszéspontját; ez a kör tehát metszi az összes egyenest. Legyen e kör sugara R és vezessük be az e_n+1=e₁ jelölést is. Jelölje az e_i és e_i+1 egyenesek hajlásszögét $\displaystyle alpha$_i és legyen t_i a P_i pont O-tól vett távolsága. Állítjuk, hogy i=1,2,...,n esetén t_i+1<t_icos$\displaystyle alpha$_i+2R.

Valóban, ha az e_i és e_i+1 egyenesek a Q_i pontban metszik egymást, akkor

t_i+1$\displaystyle le$Q_iP_i+1+OQ_i=Q_iP_icos$\displaystyle alpha$_i+OQ_i$\displaystyle le$(OP_i+OQ_i)cos$\displaystyle alpha$_i+OQ_i=

=t_icos$\displaystyle alpha$_i+OQ_i(1+cos$\displaystyle alpha$_i)<t_icos$\displaystyle alpha$_i+2R.

Ha pedig a két egyenes párhuzamos, akkor O-hoz legközelebbi pontjukat (mely a körön belül van) Q_i'-vel, illetve Q_i''-vel jelölve

t_i+1$\displaystyle le$Q_i''P_i+1+OQ_i''=Q_i'P_i+OQ_i''$\displaystyle le$OP_i+OQ_i'+OQ_i''<t_i+2R.

Így indukcióval könnyen ellenőrizhető, hogy

t_i$\displaystyle le$t₁cos$\displaystyle alpha$₁...cos$\displaystyle alpha$_i-1+(i-1)2R,

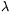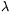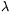vagyis OP_n+1$\displaystyle le$ $lambda$ OP₁+2nR, ahol 0 $le$ $lambda$ =cos $alpha$ ₁...cos $alpha$ _n<1. Ezért ha OP₁>2nR/(1- $lambda$ ), akkor OP_n+1<OP₁.

Vegyünk fel most egy koordinátarendszert, melynek középpontja O, egyik tengelye pedig e₁. Egy x valós számra legyen P₁=P₁(x) az e₁ egyenesnek azon pontja, melynek első koordinátája x, és legyen x' az ehhez tartozó P_n+1=P_n+1(x) pont első koordinátája. Az f(x)=x-x' függvény folytonos a valós számegyenesen, továbbá f(x)>0, ha x>2nR/(1-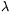 $lambda$ ) és f(x)<0, ha x<2nR/(1- 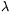$lambda$ ). Van tehát olyan x valós szám, melyre f(x)=0, az ehhez tartozó P₁=P₁(x) pont megfelelő lesz.

B.3560. Bizonyítsuk be, hogy bárhogyan is hagyunk el az első 2002 pozitív egész szám közül 89 darabot, a megmaradó számok között van 20 olyan, amelyeknek az összege is a megmaradt számok között van. (5 pont)

Megoldás: Először is jegyezzük meg, hogy 20 darab 109-nél nem nagyobb pozitív egész szám összege legalább 1+2+...+20>109, de legfeljebb 90+91+...+109<2002. Tegyük fel, hogy az első 109 pozitív egész szám közül 89-k darabot hagytunk el, a 110 és 2002 közé eső számok közül pedig k darabot (0 $le$ k $le$ 89). Ha k=0, akkor az első 109 szám közül még megmaradt 20, melyek összege 110 és 2002 közé esik, és így szerepel a megmaradt számok között. Ha 1 $le$ k $le$ 4, akkor az első 101 szám közül legalább 21 megmaradt. 21 megmaradt számból egy-egy elhagyásával 21 különböző 20-tagú összeget készíthetünk, melyek mindegyike 110 és 2002 közé esik. Ezen összegek közül tehát legalább 21-k $ge$ 17 szerepel a megmaradt számok között.

Végül ha k $ge$ 5, akkor az első 109 számból megmaradt legalább 25, legyen a₁<a₂<...<a₂₅ ezek közül 25. Azt állítjuk, hogy e számokból legalább 101 különböző 20-tagú összeget készíthetük. Valóban, induljunk ki az a₁+...+a₁₉+a₂₀ összegből. Az utolsó tag helyére rendre a₂₁-et, ..., a₂₅-öt írva egyre nagyobb összegeket kapunk:

a₁+...+a₁₉+a₂₀<a₁+...+a₁₉+a₂₁<...<a₁+...+a₁₉+a₂₅.

Ez eddig 6 különböző összeg. Növeljük ezek után a₁₉-et 5 lépésben a₂₄-re:

a₁+...+a₁₈+a₁₉+a₂₅<a₁+...+a₁₈+a₂₀+a₂₅<...<a₁+...+a₁₈+a₂₄+a₂₅,

ez 5 újabb összeget eredményez. Az eljárást az a₁₈,a₁₇,...,a₁ összeadandókkal is elvégezve végül 20-tagú összegek 101 elemű szigorúan növő sorozatához jutunk. Minden ilyen összeg 110 és 2002 közé fog esni, ahonnan csak k $le$ 89 számot hagytunk el, közülük tehát legalább 101-89=12 kell, hogy szerepeljen a megmaradt számok között.

B.3561. Egy konvex poliéder minden csúcsából pontosan három él indul ki. Egy lap kivételével a poliéder minden lapjáról tudjuk, hogy van körülírt köre. Bizonyítsuk be, hogy ekkor a poliéder valamennyi lapjának van körülírt köre. (5 pont)

Megoldás: Legyen K a poliéder azon lapja, amelyről még nem tudjuk, hogy van-e körülírt köre, S pedig a K-ra illeszkedő sík. Tekintsük P-nek S-től legtávolabb eső csúcsait, legyen ezek száma k. Ha k=1, akkor jelölje az egyetlen ilyen csúcsot V₁. Ha k=2, akkor ezeket a csúcsokat egy él köti össze; a két csúcsot jelölje V₁ és V₂. A k $ge$ 3 eset pedig pontosan akkor fordul elő, ha P-nek van egy K-val párhuzamos K' lapja, melynek csúcsait valamely körüljárás szerint jelölje V₁,V₂,...,V_k. A poliéder csúcsai ezek után legyenek V₁,V₂,...,V_n, ahol 1 $le$ i<j $le$ n esetén teljesül, hogy V_i legalább olyan távol van S-től, mint V_j.

P minden K-tól különböző lapjának jelöljük ki a legkisebb indexű csúcsát, legyen ez $phi$ (L). Ekkor L minden csúcsa legfeljebb olyan távol van S-től, mint $phi$ (L). Vizsgáljuk meg, hogyan lehet két különböző L,L' lapra $phi$ (L)= $phi$ (L'). Ha $phi$ (L)= $phi$ (L')=V, akkor a V-ből induló 3 él, melyek közül az egyik az L és az L' lapnak is éle, végig az S sík és az azzal párhuzamos, V-re illeszkedő sík között halad; P konvex volta miatt tehát P minden csúcsa e két sík között helyezkedik el, vagyis V=V_i valamely 1 $le$ i $le$ k esetén. Innen pedig már könnyen belátható, hogy ekkor szükségképpen V=V₁.

Legyen most L₁,L₂,...,L_m a poliéder K-tól különböző lapjainak sorbarendezése úgy, hogy ha i<j, $phi$ (L_i)=V és $phi$ (L_j)=V, akkor $alpha$ $le$ $beta$ . Ekkor L₁, L₂, L₃ éppen a V₁ csúcsot tartalmazó 3 lap, a többi lap sorrendje pedig már egyértelmű, és az is igaz, hogy i<j esetén az L_i lap S-től legtávolabb fekvő csúcsa legalább olyan messze van S-től, mint az L_j lap megfelelő csúcsa.

Jelöljük O_i-vel az L_i lap köré írt kör középpontját, E_i-vel pedig az L_i síkjára merőleges, O_i-n áthaladó egyenest; ez azon pontok mértani helye, melyektől az L_i lap minden csúcsa ugyanolyan távol van. Ebből adódik, hogy ha az L_i,L_j,L_l lapoknak van egy közös csúcsa, akkor az E_i,E_j,E_l egyenesek egy ponton mennek át. Legyen tehát O az E₁,E₂,E₃ egyenesek metszéspontja, G pedig az O középpontú, V₁-en áthaladó gömb. Az alábbiakban megmutatjuk, hogy minden 1 $le$ i $le$ m esetén E_i áthalad O-n és az L_i lap minden csúcsa illeszkedik G-re. Ebből ugyanis már következik, hogy P minden csúcsa a G gömbön helyezkedik el, és így a K lapnak is van körülí rt köre, nevezetsen az S sík G-vel alkotott metszete.

Az állítás i=1,2,3 esetén igaz. Tegyük fel tehát, hogy 3<j $le$ m, és az állítást i<j esetén már igazoltuk. Legyen $phi$ (L_j)=V, és L_s,L_t,L_j a P-nek V-ra illeszkedő lapjai. Ha $phi$ (L_s)=V és $phi$ (L_t)=V, akkor $phi$ definíciója és a lapok sorbarendezése alapján megállapíthatjuk, hogy $alpha$ , $beta$ $le$ $gamma$ , sőt $gamma$ $ne$ 1 miatt $alpha$ , $beta$ < $gamma$ is igaz. Ezért s,t<j, és így az indukciós feltevés alapján az E_s,E_t egyenesek O-ban metszik egymást, a V csúcs pedig G-n helyezkedik el. Mivel ez a csúcs az L_s,L_t és L_j lapoknak is csúcsa, az E_s,E_t,E_j egyenesek egy ponton mennek át, ami nem lehet más, mint O. Ezért L_j minden csúcsa ugyanolyan távol van O-tól, mint V, tehát illeszkedik G-re. Vagyis az állítás i=j esetén is teljesül, amivel az indukciós lépés helyességét igazoltuk, a bizonyítást befejeztük.

Már regisztráltál?
Új vendég vagy?