Solutions for exercises "C" in May, 2002

In this page only the sketch of the solutions are published; in some cases only the final results. To achieve the maximum score in the competition more detailed solutions needed.

C. 675. Is there a square number in which the last two digits are both odd?

Solution. The number in question can only be the square of an odd number, of the form (2k+1)²=4k(k+1)+1, thus it leaves a remainder of 1 when divided by 4 (or even by 8). The last digit of an odd square number may be 1, 5 or 9, which now means that the remainder is 11, 15 or 19 when the number is divided by 20. Such numbers, however leave a remainder of 3 when divided by 4, and that contradicts to the observation above. Therefore, the last two digits of a square number cannot both be odd.

C. 676. The length of side AB of the rectangle ABEF is 1 unit, and the length of side BE is 3 units. The points C and D divide side BE into three equal parts. Show that BAC+BAD$\displaystyle \angle$+BAE=180^o.

Solution.

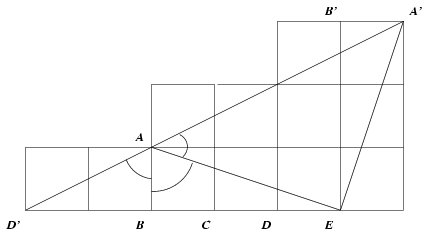
The figure shows that BAD'$\displaystyle mangle$=BAD$\displaystyle mangle$ and BAC$\displaystyle mangle$=45^o=EAA'$\displaystyle mangle$, thus BAD$\displaystyle mangle$+BAE$\displaystyle mangle$+BAC$\displaystyle mangle$=D'AB$\displaystyle mangle$+BAE$\displaystyle mangle$+EAA'=180^o. (The problem can also be solved by using the addition formula of the tangent function.)

C. 677. Find the integers a and b, given that a⁴+(a+b)⁴+b⁴ is a square number.

Solution. A square number may leave a remainder of 0 or 1 when divided by 4. 0 if the number is even and 1 if it is odd. Thus there is at most one odd number among a, b, and a+b. That can only happen if a and b are both even: a=2a₁, b=2b₁. Hence if a⁴+(a+b)⁴+b⁴=16(a₁⁴+(a₁+b₁)⁴+b₁⁴) is a perfect square, then so is a₁⁴+(a₁+b₁)⁴+b₁⁴. That makes a₁ and b₁ also even, and so on. It follows that a and b are divisible by every power of 2, which is only possible if a=b=0; and that satisfies the requirement of the problem, too.

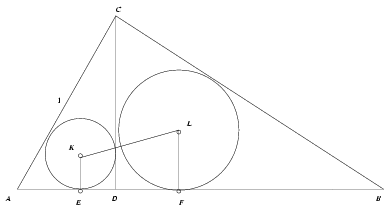
C. 678. In a triangle ABC, AC=1, ABC$\displaystyle \angle$=30^o, BAC=60^o, and D denotes the foot of the altitude from vertex C. Find the distance between the centres of the inscribed circles of the triangles ACD and BCD.

Solution.

ABC

is a (special) right-angled triangle, $\displaystyle BC=\sqrt{3}$, AB=2^.AC=2. The perimeter of the triangle ACD is $\displaystyle k_{ACD}={1\over2}k_{ABC}={{3+\sqrt{3}}\over2}$, and similarly, $\displaystyle k_{BCD}={{\sqrt{3}}\over2}k_{ABC}={{3+3\sqrt{3}}\over2}$. The corresponding areas are $\displaystyle t_{ACD}={1\over4}t_{ABC}={1\over4}\cdot{{\sqrt{3}}\over2}={{\sqrt{3}}\over8}$, $\displaystyle t_{BCD}={3\over4}t_{ABC}={3\over4}\cdot{{\sqrt{3}}\over2}={{3\sqrt{3}}\over8}$. Thus the radii of the incircles of the small triangles are $\displaystyle KE={{2\cdot t_{ACD}}\over{k_{ACD}}}={{\sqrt{3}}\over4}/{{3+\sqrt{3}}\over2}={{\sqrt{3}-1}\over4}$, $\displaystyle LF={{2\cdot t_{BCD}}\over{k_{BCD}}}={{3\sqrt{3}}\over4}/{{3+3\sqrt{3}}\over2}={{3-\sqrt{3}}\over4}$. Finally, $\displaystyle ED={{k_{ACD}}\over2}-AC={{3+\sqrt{3}}\over4}-1={{\sqrt{3}-1}\over4}$, $\displaystyle DF={{k_{BCD}}\over2}-BC={{3+3\sqrt{3}}\over4}-\sqrt{3}={{3-\sqrt{3}}\over4}$, thus it follows from the Pythagorean theorem that $\displaystyle KL=\sqrt{EF^2+(LF-KE)^2}=\sqrt{{1\over4}+{{(2-\sqrt{3})^2}\over4}}={2-\sqrt{3}}\approx0.52$.

C. 679. Given three spheres that pairwise touch each other and also touch the plane S, determine the radius of the sphere that has its centre on the plane S, and that touches all the three spheres.

Solution.

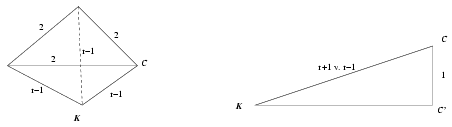
The centres of the three unit spheres form an equilateral triangle of side length 2 in a plane parallel to the plane S at a distance of 1. The distance of the centre K of the sphere of radius r in question from all three vertices of the triangle is r$\displaystyle pm$1, depending on whether it touches the spheres on the outside or on the inside. Let C denote one of the three centres, and let C' be its orthogonal projection onto the plane S. It follows from the Pythagorean theorem applied to the right triangle KC'C that $\displaystyle KC'=\sqrt{KC^2-C'C^2}=\sqrt{(r\pm1)^2-1}=\sqrt{r^2\pm2r}$. On the other hand, the length of KC' is equal to the distance $\displaystyle {2\over{\sqrt{3}}}$ of the centre of the equilateral triangle of 2-unit side from the vertices. Hence $\displaystyle r^2\pm2r={4\over3}$, thus $\displaystyle r={{\sqrt{21}\pm3}\over3}$. So far, we have been assuming that the sphere in question either touches all the unit spheres on the outside or it touches all of them on the inside. There is no "mixed" configuration, because if the sphere of radius r of centre K touched the sphere of centreG₁ on the outside and the sphere of centre G₂ on the inside, then KG₁=r+1, KG₂=r-1 would imply that G₁G₂=2=(r+1)-(r-1)=KG₁-KG₂, that is, the triangle G₁G₂K would be degenerate, which means that K would lie on the line G₁G₂. That line, however, is parallel to the plane S, and thus has no common point with it.