A számítástechnika-versenyben kitűzött feladatok 2002. május

Kérjük, olvassa el a versenykiírást.

I. 25. A Zeckendorf tétel alapján minden természetes szám egyértelműen előállítható Fibonacci számok összegeként úgy, hogy n =F_k1 + F_k2 + ...+ F_kr, ahol i (1 \(\displaystyle \le\)i <r): k_i \(\displaystyle \ge\)k_i+1 + 2, és k_r \(\displaystyle \ge\)2. A Fibonacci számokat az alábbi módon számolhatjuk:

\(\displaystyle F_k=\cases{0{\rm\ ha\ }k=0\cr1{\rm\ ha\ }k=1\cr F_{k-1}+F_{k-2}{\rm\ ha\ }\)1.} ">

Készítsünk programot (I25.PAS,...), amely adott n (1 \(\displaystyle \le\)n \(\displaystyle \le\)10 000 000) természetes számot felbont Fibonacci számok összegére! (A megoldásban a hatékonyságot is értékeljük.) (10 pont)

I. 26. A Sierpinski csipke egy rekurzív ábra, ami úgy keletkezik, hogy első lépésben egy négyzet alakú terítőből kivágjuk a középső, harmad akkora oldalhosszúságú négyzetet. Ez a csipke 1. szintje. Az ezután maradt részt 8 kisebb négyzet alakú résznek véve, mindegyikre végrehajtjuk ugyanezt a műveletet. Ez lesz a 2. szint. Az eljárást a megmaradt 8^.8, kilenced akkora területtel folytatjuk tovább...

Készítsünk programot (I26.PAS,...), amely beolvassa a szint sorszámát, majd kirajzolja az adott szintű Sierpinski csipkét, szürkére színezve a megmaradt részeket!

1. szint	2. szint	3. szint	4. szint

(10 pont)

I. 27. A ,,Francia zászló'' probléma egy szabályozási feladat. Egymás mellett levő N darab, egyformán működő cellát olyan állapot-átmenet függvénnyel (cellába írandó képlettel) kell ellátni, aminek hatására az N cellában a francia zászló mintázata alakul ki: az első N/3 cella piros, a második N/3 cella fehér, a harmadik N/3 cella pedig kék színű lesz.

A kiinduló állapotban a bal szélső cellát impulzus éri, aminek hatására három hullám (i,j,k) indul ki belőle. Minden cellában 1 időegységig tartózkodik az i-hullám, majd továbblép a jobb oldali szomszédjába, a j-hullám 2, a k-hullám pedig 5 időegységig tartózkodik egy-egy cellában, mielőtt a következőbe jut. Az i-hullám a jobb szélső cellából visszaverődik és kiolt minden hullámot, amivel találkozik.

Ha egy cellát i-hullám ér, akkor az eredetileg szürke cella kék színű lesz, ha j-hullám éri, akkor fehér, ha pedig k-hullám, akkor piros. Ha a visszavert i-hullám ér egy cellához, akkor annak színe a továbbiakban nem változik. Az ábrákon az egyes lépéseknek az egyes sorok felelnek meg. (Az ábrák a lap hátsó borítóján találhatók.)

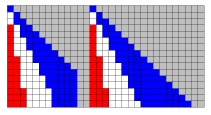1. ábra	2. ábra	3. ábra

Ha a bal szélső cellát újabb impulzus éri, akkor újra elindítja az i-, j- és k-hullámot, s a mintázat újra kialakul (2. ábra). Ha pedig a cellasort szétszakítjuk (beszúrunk a táblázatba egy üres oszlopot), akkor a mintázat külön-külön mindkét részben kialakul. (3. ábra)

Készítsünk Excel állományt (I27.XLS) a ,,Francia zászló'' probléma megoldására. (10 pont)

A számítástechnika feladatok megoldásai a következő címre küldendők:

A beküldési határidő: 2002. június 13.