New exercises and problems in Mathematics
September 2002

Please read The Conditions of the Problem Solving Competition.

New exercises

Maximum score for each exercise (sign "C") is 5 points.

C. 680. A committee of nine members was set up to choose one out of three candidates. They used the following procedure: every member of the committee ranked the candidates, giving 3 points to the first one, 2 to the second one, and 1 to the third one. When the points were added, the sums were all different, which clearly established the order of the candidates. However, one member of the committee noticed that if each of them had selected only one candidate and given 1 point to that candidate, the final order of the candidates would have been reversed. How many points did each candidate (originally) get?

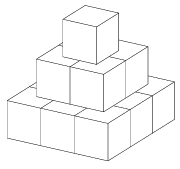
C. 681. The ``pyramid'' in the figure is built out of three layers of 1 cm³ cubes, its surface area is 42 cm². Using the same technique, we also built a larger ``pyramid'' with total surface area of 2352 cm². How many layers does it consist of?

C. 682. In 2002, the tax paid by those with an annual gross income of more than 1,050,000 forints (HUF) was 40% of the amount over 1,050,000 forints plus 267,000 forints. For what gross annual income was the tax equal to 30% of the income? (E. Fried, Budapest)

C. 683. In the isosceles right triangle ABC, AC=BC. the angle bisector drawn from vertex A intersects the leg BC at the point P. Prove that the length of the line segment PB is equal to the diameter of the inscribed circle of ABC.

C. 684. Solve the simultaneous equations

x-xy+y=1, x²+y²=17.

New problems

The maximum scores for problems (sign "B") depend on the difficulty. It is allowed to send solutions for any number of problems, but your score will be computed from the 6 largest score in each month.

B. 3562. For her birthday, an eight-year-old little girl was given a cake shaped like a right prism of a convex heptagonal base. The cake is cut into pieces with vertical cuts along some of its diagonals. The little girl wants an octagonal piece. Is that possible? (3 points)

B. 3563. For what minimum value of t is the inequality $\displaystyle \sqrt{xy}\leq t(2x+3y)$ true for all non-negative real x, y? (3 points)

B. 3564. Move the point A(0;1) of the (x,y) coordinate plane onto the point B(3;2) by an appropriate composition of reflections about the x-axis and rotations about the point A. (4 points)

B. 3565. We are given 2002 boxes with a few pebbles in each, and we are also given a large (inexhaustible) heap of pebbles. In each step, we are allowed to put one pebble into each of any set of k boxes. Is it possible to achieve that there are the same number of pebbles in every box if

a) k=8;

b) k=9? (4 points)

B. 3566. For every interior point P in a given triangle ABC, a triangle can be constructed out of the line segments PA, PB and PC. Show that the triangle ABC is equilateral. (4 points)

B. 3567. Given that each side of a convex pentagon is parallel to one of its diagonals, what may be the ratio of the length of a side to that of the parallel diagonal? (5 points)

B. 3568. Find the angle $alpha$ , given that for every non-negative integer k, cos2^k $alpha$ $le$ 0. (5 points)

B. 3569. Given that any two out of 100 given cubes have a common interior point, and each of the edges is parallel to one of three given lines, show that the cubes have a common interior point. Give an example of 100 cubes, such that any three of them have a common interior point but there is no point contained in every cube. (5 points)

B. 3570. f is a continuous function, f(1000)=999 and f(x)^.f(f(x))=1 for every real number x. Find the value of f(500). (4 points)

B. 3571. A cup shaped like a right truncated cone is rolled around on a round table, so that the cup never touches the edge of the table. The diameter of the table is 1.6 metres. The diameter of the base of the cup is 5 cm, that of the top is 6.5 cm. What is the height of the cup? (4 points)

New advanced problems

Maximum score for each advanced problem (sign "A") is 5 points.

A. 296. Alice has chosen one of the numbers 1,2,...,16. Bob can ask seven yes-no questions to find it out. Alice is allowed to give at most one wrong answer. Help Bob to find out the number in all cases.

A. 297. Let a₀,a₁,... be positive integers such that a₀=1, a₁>1 and

$\displaystyle a_{n+1}=\frac{a_1\cdot\ldots\cdot a_n}{a_{[n/2]}}+1$

for all n=1,2,.... ([x] denotes the integer part of x.) Show that $\displaystyle \sum_{n=1}^\infty\frac{1}{a_{n+1}a_{[n/2]}}$ is a rational number.

A. 298. The angles of a spherical triangle are $\displaystyle alpha$, $beta$ and $gamma$ , the lengths of the opposite side arcs are a, b and c, respectively. Prove that a^.cos $beta$ +b^.cos$\displaystyle alpha$<c.

Send your solutions to the following address:

or by e-mail to:

solutions@komal.hu

Already signed up?
New to KöMaL?