 |
Solutions for advanced problems "A" in October, 2002 |
In this page only the sketch of the solutions are published; in some cases only the final results. To achieve the maximum score in the competition more detailed solutions needed.
A. 299. P and Q are interior points of the square ABCD such that PAQ\(\displaystyle \angle\)= PCQ\(\displaystyle \angle\)= 45o. Determine the length PQ in terms of the lengths BP and DQ.
Solution. Let BP=p, DQ=q and PQ=x. x needs to be expressed in terms of the lengths p and q.
One of the points P and Q lies in the interior of the triangle ABC, and the other in the interior of the triangle ACD. Thus there are two cases:
1. If P lies inside triangle ABC and Q lies inside triangle ACD then the orientations of both triangle APQ and triangle CQP are the same as that of the square ABCD.
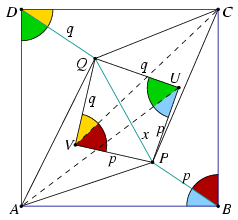
Reflect the point B in the lines AP and CP; let the reflections be U and V, respectively. It follows from the reflection that AU=AB=AD, and by adding up the angles at vertex A we have QAU\(\displaystyle \angle\)=DAQ\(\displaystyle \angle\). Hence the triangles AQU and AQD are congruent. Analogously, the triangles CQV and CQD are also congruent.
It follows from the conruences that the angles marked with the same colour in the Figure are equal, PU=PV=PB=p and QU=QV=QD=q. The triangles PQU and PQV are congruent because they have pairwise equal sides. Thus their angles at U and V are equal. the sum of these two angles equals the sum of the angles of the square ABCD at B and D, therefore PUQ\(\displaystyle \angle\)=PVQ\(\displaystyle \angle\)=90o. Hence with the Pythagorean theorem
\(\displaystyle x=\sqrt{p^2+q^2}.\)
It also follows from the reasoning that the angles marked blue and yellow are equal, so are the angles marked red and green, and the line segment BP is parallel to QD.
2. If Q lies iside the triangle ABC and P inside the triangle ACD then the triangles APQ and CQP both have the orientation opposite to that of the square ABCD. In that case, the solution is more complicated (and so is the result).
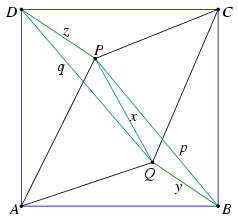
As seen above, the quadrilateral QBPD is a trapezium, its bases are QB and PD, and PQ2=BQ2+DP2. It also follows from the arrangement of the points that BP>DP and BQ<DQ.
We will first show that for every trapezium of this kind, there are suitable points A and C, such that ABCD is a square and PAQ\(\displaystyle \angle\)=PCQ\(\displaystyle \angle\)=45o.
Let therefore QBPD be a trapezium in which PQ2=BQ2+DP2. Let U and V be the two points with QU=QV=BQ and PU=PV=DP; let U lie on the same side of the diagonal PQ as the point B, and let V lie on the same side as the vertex D. The converse of the Pythagorean theorem implies that PUQ\(\displaystyle \angle\)=PVQ\(\displaystyle \angle\)=90o.
Let A be the intersection of the bisectors of the angles BQU and DPU, and let C be the intersection of the bisectors of the angles BQV and DPV.
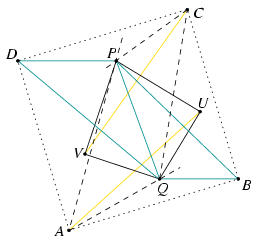
The line segments AB, AU and AD are equal in length since they are symmetrical about the lines AQ and AP. Similarly, CB=CV=CD because these three line segments are symmetrical about the lines CQ and CP. By adding up the angles of the hexagons ABQUPD and CDPVQB we have PAQ\(\displaystyle \angle\)=PCQ\(\displaystyle \angle\)=45o and PAD\(\displaystyle \angle\)=BCD\(\displaystyle \angle\)=90o. Hence the quadrilateral ABCDis a square.
It follows from the conditions BP>DP and BQ<DQ that the points U and V lie between the arms of the angles PQB and QPD, respectively. The points A and B as well as the points C and D lie on opposite sides of the line PQ, and the square ABCD really contains the line segment PQ in its interior.
Let a denote the side length of the square-val, and let BQ=y, QD=z. We are going to express x in terms of the lengths of the line segments a, p, q. The arrangement of the points shows that \(\displaystyle {1\over\sqrt2}a As seen above, x2=y2+z2. The line segment BD is the diagonal of the square, thus \(\displaystyle BD=\sqrt2a\). Consider the trapezium QBPD. Let QBP\(\displaystyle \angle\)=\(\displaystyle \beta\) and PDQ\(\displaystyle \angle\)=\(\displaystyle \delta\). Apply the cosine rule to the triangles QBP, BPD, PDQ and DQB: x2=p2+y2-2pycos \(\displaystyle \beta\) 2a2=p2+z2+2pzcos \(\displaystyle \beta\) x2=q2+z2-2qzcos \(\displaystyle \delta\) 2a2=q2+y2+2qycos \(\displaystyle \delta\) By eliminating the cosines, we have Divide the sum of the equations (1) and (2) by (y+z): x2+2a2=p2+q2+2yz, and hence (y-z)2=x2-2yz=p2+q2-2a2 and (y+z)2=x2+2yz=2x2+2a2-p2-q2. Square the difference of the equations (1) and (2): (2a2-x2)2(y-z)2=(p2-q2)2(y+z)2 (2a2-x2)2(p2+q2-2a2)=(p2-q2)2(2x2+2a2-p2-q2) The number 2a2-x2 can be calculated from this equation (quadratic at most). The leading coefficient is non-negative: p2+q2-2a2=(y-z)2\(\displaystyle \ge\)0. If the leading coefficient is 0, that is p2+q2-2a2=(y-z)2=0, then y=z, the quadrilateral QBPD is a parallelogram, and p=q=a. It is easy to see that if P and Q lie on the circles of radius a centred at B and D, respectively, symmetrically about the centre of the square then PAQ\(\displaystyle \angle\)=PCQ\(\displaystyle \angle\)=45o will be true. In that case all we know about the length of the line segment PQ is that it lies in the interval \(\displaystyle [(2-\sqrt2)a,\sqrt2a)\). If the leading coefficient is positive then the quadratic formula can be applied to the equation (3). Since the constant term is negative, the equation has one positive and one negative root.We also know that \(\displaystyle x<\sqrt2a\), that is, 2a2-x2>0, thus we need the positive root: \(\displaystyle 2a^2-x^2={-(p^2-q^2)^2+\sqrt{(p^2-q^2)^4+
(p^2+q^2-2a^2)(p^2-q^2)^2(6a^2-p^2-q^2)}\over p^2+q^2-2a^2}=\) \(\displaystyle ={-(p^2-q^2)^2+2|p^2-q^2|\sqrt{-3a^4+2a^2(p^2+q^2)-p^2q^2}
\over p^2+q^2-2a^2},\) \(\displaystyle x=\sqrt{2a^2+{(p^2-q^2)^2-2|p^2-q^2|\sqrt{-3a^4+2a^2(p^2+q^2)-p^2q^2}
\over p^2+q^2-2a^2}}.\)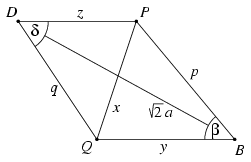
(1) x2z+2a2y=(p2+yz)(y+z),
(2) x2y+2a2z=(q2+yz)(y+z).
(3) (p2+q2-2a2)(2a2-x2)2+2(p2-q2)2(2a2-x2)-(p2-q2)2(6a2-p2-q2)=0. 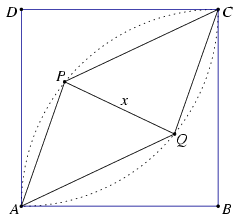
A. 300. Find all pairs (a, b) such that a and b are whole numbers and a2 + ab + b2is a multiple of 75.
Solution. Consider the following identities:
| (2.1) | (x-2y)(2x-y)=2(x2+xy+y2)-7.xy; |
| (2.2) | (x-18y)(18x-y)=18(x2+xy+y2)-73.xy; |
| (2.3) | (x-1353y)(1353x-y)=1353(x2+xy+y2)-109.75.xy. |
It follows that a2+ab+b2 is only divisible by 75 if any of the following conditions holds:
- a and b are both divisible by 73;
- a=72p, b=72q, where p\(\displaystyle \equiv\)2q (mod 7) or q\(\displaystyle \equiv\)2p (mod 7);
- a=7p, b=7q, where p\(\displaystyle \equiv\)18q (mod 73) or q\(\displaystyle \equiv\)18p (mod 73);
- a\(\displaystyle \equiv\)1353b (mod 75) or b\(\displaystyle \equiv\)1353a (mod 75).
A. 301. Let a0,a1,... a sequence of non negative numbers such that for every k, m \(\displaystyle \ge\)0, ak+m \(\displaystyle \le\)ak+m+1 + ak am. Assume, additionally, that nan < 0.2499 holds for sufficiently large n. Prove that there exists a number q for which 0<q<1 and an<qn if n is large enough.
Solution. Let p=0,2499 and let \(\displaystyle 1 For every N\(\displaystyle \ge\)n0 let \(\displaystyle S(N)=\sup\{na_n:~n\ge k\}\). With the choice of n0, for example, S(n0)\(\displaystyle \le\)p. If N\(\displaystyle \ge\)n0 and n\(\displaystyle \ge\)2N, then \(\displaystyle na_n=n\sum_{k=n}^\infty(a_k-a_{k+1})\le n\sum_{k=n}^\infty a_{[k/2]}a_{[(k+1)/2]}\le n\sum_{k=n}^\infty{S(N)\over\big[{k\over2}\big]}
\cdot{S(N)\over\big[{k+1\over2}\big]}<\) \(\displaystyle This is true for all n\(\displaystyle \ge\)2N, therefore \(\displaystyle S(2N)=\sup\{na_n:~n\ge2N\}\le4rS^2(N),\) that is, 4rS(2N)\(\displaystyle \le\)(4rS(N))2. By repeated application of the above, we get \(\displaystyle S(2^mN)\le{1\over4r}\big(4rS(N)\big)^{2^m}<
\big(4rS(N)\big)^{2^m}.\) Now let n>n0 be an arbitrary positive integer. Let m be a non-negative integer, such that 2mn0\(\displaystyle \le\)n<2m+1n0 should be true. Then \(\displaystyle a_n\le{1\over n}S(2^mn_0)<
{1\over n}\big(4rS(n_0)\big)^{2^m}<
\big(4pr\big)^{2^m}<
\big(4pr\big)^{n/2n_0}
\le\left(\root{2n_0}\of{4pr}\right)^n.\) Since the number r was chosen to make 4pr<1 true, the number \(\displaystyle q=\root{2n_0}\of{4pr}\) satisfies the requirement of the problem..
