Exercises and problems in Physics
October 2002

Please read The Conditions of the Problem Solving Competition.

Experimental problem

M. 236. In the vinification process new wine is drawn from an upper barrel into a lower one through a rubber hose. Model this process with water. Examine the dependence of the water stream velocity on the level difference and on the length of the hose. (6 points)

Theoretical problems It is allowed to send solutions for any number of problems, but final scores of students of grades 9-12 are computed from the 5 best score in each month. Final scores of students of grades 1-8 are computed from the 3 best scores in each month.

P. 3551. A crane driven by a toy DC electromotor is lifting a load of a mass of 200 g with 0.2 m/s velocity. What is the power of the crane's electromotor if 10% of the overall power goes against the friction? How much is the current drain of the 9 V electromotor if its efficiency is 80%? (4 points)

P. 3552. We try to measure the depth of a well on the basis of the delay of the splash of a stone we have dropped in. What is the error of the depth measurement if the error of our time measurement is p %? Neglect the aerodynamic drag and the time of sound propagation. When is it allowable to discard these data? (4 points)

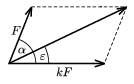
P. 3553. Add forces of magnitude F and kF including an $\displaystyle \alpha$ angle with each other (k1). At what angle , the angle of the resultant force and component kF, will be the greatest? What is this angle? (5 points)

P. 3554. We release a solid ball and a cylinder from the top of a slope at the same time. Can they reach the bottom at the same time as well? (4 points)

P. 3555. We stand in front of a wall. Between us and the wall, at the height of our ears, there is a whistle blowing, at a frequency of 600 Hz. How fast must the whistle go towards the wall so that we can hear 3 beats a second? (4 points)

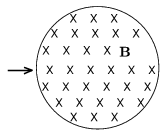
P. 3556. Inside the air-gap of a toroidal coil the magnetic field has a circular cross section and it can be considered homogeneous. If charged particles are coming in a radial direction perpendicular to the magnetic field lines, do the slower or the faster ones leave the magnetic field in a shorter time? (5 points)

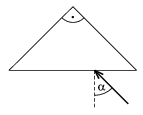
P. 3557. A light beam is falling on the hypotenuse of a rectangular symmetric glass prism from the air. Choose the $\displaystyle \alpha$ angle of incidence so that total reflection will occur at both opposing sides (n=1.5). a) Determine the angle included by the beams incoming and leaving the prism. b) What maximum value can we choose for angle , so that total reflections still occur? (5 points)

P. 3558. In an atomic reactor the slow, thermal neutrons cause atomic fissions with a greater probability than the faster ones. Therefore, the neutrons emerging from fission processes must be decelerated (moderated) with deuterium oxide or graphite. Determine what fraction of its energy does a neutron lose in a straight elastic collision with a ²₁H and a $\displaystyle {}^{12}_{\phantom{1}6}\rm C$ atomic nucleus. (4 points)

P. 3559. Estimate what percentage of the area of Hungary has to be covered with modern (50% efficiency) solar panels if the current electric power need of the country (7 GW on average) is to be supplied by them. (5 points)

P. 3560. There is a 1 m long horizontal rod. One of its ends is fixed and on the other a body of a mass of 1 kg is hung causing a 1 cm deflection. Estimate the force F under which the same, vertically placed rod collapses. (Hint: the elastic energy of a bent rod is proportional to its length and inversely proportional to the square of the radius of curvature.) (6 points)

Send your solutions to the following address:

KöMaL Szerkesztőség (KöMaL feladatok),
Budapest 112, Pf. 32. 1518, Hungary

solutions@komal.elte.hu.

Deadline: 11 November 2002