 |
Exercises and problems in Informatics |
Please read The Conditions of the Problem Solving Competition.
I. 31. In ancient Egypt rational
numbers between 0 and 1 were represented by a sum of unit fractions
\(\displaystyle \frac{1}{x_1}+\frac{1}{x_2}+\ldots+\frac{1}{x_k}\) with
xi's being different positive
integers. Examples: \(\displaystyle \frac{2}{5}=\frac{1}{3}+\frac{1}{15}\),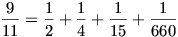 
,
\(\displaystyle \frac{19}{30}=\frac{1}{2}+\frac{1}{8}+\frac{1}{120}\).
Your program (I31.pas, ...) should convert a given rational number \(\displaystyle \frac{M}{N}\) (1\(\displaystyle \le\)M<N, 2\(\displaystyle \le\)N \(\displaystyle \le\)30) to unit fraction form. (10 points)
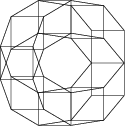
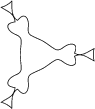
I. 32. A bipolygon is obtained by merging the edges of two regular polygons, that is by alternately drawing their edges. (In the figure we merged a square and a triangle by drawing 3 edges of each. We may draw 4 edges as well by connecting the vector U3 to V2 and V0 to U3.)
A multipolygon is produced similarly using more than 2 regular polygons.
 |
 |
 |
 |
| DB=2, N=3 H=50, SZ=90 H=50, SZ=120 |
DB=2, N=40 H=50, SZ=90 H=50, SZ=-40 |
DB=2, N=360 H=0.5, SZ=1 H=1, SZ=-1 |
DB=4, N=360 H=1, SZ=1 H=1, SZ=-8 H=1, SZ=16 H=1, SZ=-2 |
Write your program (I33.pas, ...) which reads the
number of polygons to be merged (1\(\displaystyle \le\)DB \(\displaystyle \le\)100), the number of edges to be drawn of
each polygon (1\(\displaystyle \le\)N \(\displaystyle \le\)360), the lengths of the edges and the exterior angles of
the polygons (1\(\displaystyle \le\)H(i)\(\displaystyle \le\)100 and -120\(\displaystyle \le\)S(i) 
120, respectively),
then draws the corresponding multipolygon.
See an example on the figure. (10 points)
I. 33. Alice and Bob are playing the following game. First they list N (1\(\displaystyle \le\)N \(\displaystyle \le\)100) natural numbers, from which they both choose M (1\(\displaystyle \le\)M \(\displaystyle \le\)N) ones. They proceed regularly: Alice selects every Ath number (1\(\displaystyle \le\)A \(\displaystyle \le\)N) and Bob selects every Bth one (1\(\displaystyle \le\)B \(\displaystyle \le\)N). If the list ends, they continue the selection from the beginning, that is the (N+1)th number will be the first element of the list, the (N+2)th will be the second one, and so on. The winner is the player whose numbers have the greater sum.
Prepare your sheet (I34.xls) which, if N, M, A, B are given, decides the winner. The label of the winner (A or B) should be displayed in red, while that of the loser in blue. If the game ends in a draw, both letters should be black.
See an example in the table.
|
(10 points)