Matematikából kitűzött gyakorlatok és feladatok
2002. október

Kérjük, olvassa el a versenykiírást.

A C pontversenyben kitűzött gyakorlatok Minden C-jelű feladat helyes megoldásáért 5 pont jár.

C. 685. Hány liter egy 1000 m² felszínű, 1000 km magas henger térfogata?

C. 686. Egy unalmas órán Anna azzal múlatja az időt, hogy egész számokat ír egymás alá. Egy adott számból kiindulva a következő sorban vagy az előző szám jegyeinek az összegét, vagy pedig a szorzatukat írja. Ezzel a módszerrel folytatva az eljárást észrevette, hogy minden egyes felírt szám páratlan. Hány olyan legfeljebb hatjegyű kezdőérték van, amelyre teljesül, hogy minden egyes felírt szám páratlan?

C. 687. Egy négyszög csúcspontjainak koordinátái A(0;0), B(16;0), C(8;8), D(0,8). Írjuk fel annak az AC-vel párhuzamos egyenesnek az egyenletét, amelyik felezi a négyszög területét.

C. 688. Oldjuk meg az [x/2]+[x/4]=x egyenletet. ([x], az x egész része az x-nél nem nagyobb egészek legnagyobbika.)

C. 689. Oldjuk meg az

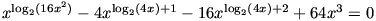
egyenletet.

Javasolta: Mosóczi András, Budapest

A B pontversenyben kitűzött feladatok A B-jelű feladatokra kapható pontszám a feladatok nehézségétől függ. Minden hónapban a 6 legnagyobb pontszám számít be a pontversenybe.

B. 3572. Oldjuk meg az [x/2]+[x/4]=[x] egyenletet. ([x], az x egész része az x-nél nem nagyobb egészek legnagyobbika.) (3 pont)

B. 3573. Adott az AB szakasz, annak F felezőpontja, valamint a P pont. Szerkesszünk P-n át AB-vel párhuzamos egyenest egyetlen vonalzó segítségével. (4 pont)

B. 3574. A k₁ kör a P pontban belülről érinti a k₂ kört. A nagyobbik kör AB húrja a kisebbik kört a C pontban érinti, AP és BP pedig a D és az E pontban metszi a kisebbik kört. Tudjuk, hogy AB=84, PD=11, végül PE=10. Mekkora az AC hossza? (4 pont)

B. 3575. Jelölje X azoknak a pozitív egészeknek a halmazát, amelyek tízes számrendszerbeli alakjában előfordulnak különböző számjegyek. Ha nX, akkor jelöljük A_n-nel azoknak a számoknak a halmazát, amelyeket az n jegyeinek az átrendezésével kapunk, d_n-nel pedig az A_n elemeinek a legnagyobb közös osztóját. Mi a d_n legnagyobb értéke? (4 pont)

B. 3576. A 0, 1, 2 számjegyekből véletlen sorozatot készítünk. Milyen hosszú sorozatok esetén lesz legalább 61% annak a valószínűsége, hogy a sorozatban mindhárom számjegy előfordul? (4 pont)

Javasolta: Fried Ervin, Budapest

B. 3577. Oldjuk meg a sin 3x + 3 cos x = 2 sin 2x (sin x + cos x) egyenletet. (4 pont)

Javasolta: Mosóczi András, Budapest

B. 3578.Az ábrán látható kocka ABCD lapjának középpontja M. Keressük meg az AB és az EM egyenesen a P illetve a Q pontokat úgy, hogy a PQ távolság egyenlő legyen az AB és az EM egyenesek távolságával.

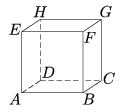
(3 pont)

B. 3579. Oldjuk meg az alábbi egyenletet:

\(\displaystyle x=\sqrt{-3+4\sqrt{-3+4\sqrt{-3+4x}}}.\)

(5 pont)

B. 3580. Tekintsük azokat a tompaszögű háromszögeket, amelyek tompaszöge az egyik hegyesszögük kétszerese, és oldalaiknak hossza egész szám. Melyiküknek a legkisebb a kerülete? (4 pont)

B. 3581. Mennyi az

f(x)=|1001+1000x+999x²+...+2x⁹⁹⁹+x¹⁰⁰⁰|

függvény legkisebb értéke? (5 pont)

Az A pontversenyben kitűzött nehezebb feladatok Minden A-jelű feladat helyes megoldásáért 5 pont jár.

A. 299. Az ABCD négyzet belsejében P és Q olyan pontok, amelyekre

PAQ\(\displaystyle \angle\)=PCQ=45^o.

Fejezzük ki a PQ szakasz hosszát a BP és DQ szakaszok hosszával!

A tanárképző főiskolások Péter Rózsa matematikaversenye, 2002

A. 300. Adjuk meg mindazokat az egészekből álló (a,b) számpárokat, amelyekre a²+ab+b² osztható 7⁵-nel.

A. 301. Legyen a₀,a₁,... nemnegatív számokból álló sorozat, amelyre tetszőleges k,m0 esetén

a_k+ma_k+m+1+a_ka_m.

Tegyük fel, hogy elég nagy n esetén na_n<0,2499. Bizonyítsuk be, hogy létezik olyan 0<q<1 szám, amelyre elég nagy n esetén

a_n<qⁿ.

Lengyel versenyfeladat

A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:

KöMaL Szerkesztőség
Budapest 112, Pf. 32.  1518

megoldas@komal.elte.hu (Az interneten keresztül történő beküldésről olvassa el tájékoztatónkat)

A beküldési határidő: 2002. november 15.