 |
A 2002 novemberi A-jelű matematika feladatok megoldása |
A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.
A. 302. Adott a síkon az egységnyi oldalú ABCD négyzet és a P pont. Bizonyítsuk be, hogy
\(\displaystyle 3AP+5CP+\sqrt5(BP+DP)\ge6\sqrt2. \)
1. megoldás. A sík tetszőleges P pontjára legyen \(\displaystyle f(P)=3AP+5CP+\sqrt5(BP+DP)\). Mivel mindegyik tag P-nek konvex függvénye, az f függvény is konvex. Ezért, ha találunk olyan pontot, ahol a függvény differenciálható és a gradiense a nullvektor, azon a helyen a függvénynek abszolút minimuma van.
A függvény gradiense
\(\displaystyle \mathop{\rm grad}f=3{\overrightarrow{AP}\over|AP|}+ 5{\overrightarrow{CP}\over|CP|}+ \sqrt5\left({\overrightarrow{BP}\over|BP|}+ {\overrightarrow{DP}\over|DP|}\right).\)
Mivel a függvény a B és D pontok felcserélésére szimmetrikus, a minimumhelyet az AC átlón érdemes keresnünk.
Egy kis számolással megkaphatjuk, hogy a minimumhely az AC átlónak a C-hez közelebbi negyedelőpontja. Ezen a helyen a gradiens tehát 0, a függvény értéke pedig, mint könnyen kiszámolható, \(\displaystyle 6\sqrt2\). Ez a függvény legkisebb értéke.
2. megoldás (Innen származik a feladat). Legyen A=(0,0), B=(1,0), C=(1,1) és D=(0,1), továbbá E=(1,5/6), F=(0,1/2), Q=(3/4,3/4), U=(-3/10,2/5) és V=(3/2,1). Mint könnyen ellenőrizhető, az U,F,Q,E,V pontok ebben a sorrendben egy egyenesre esnek, valamint az A,Q,D,U, illetve B,V,C,Q pontok egy körön vannak.
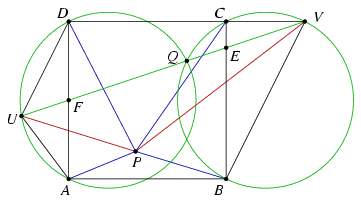
A Ptolemaiosz-tétel szerint AU.DP+DU.AP\(\displaystyle \ge\)AD.UP=UP, és egyenlőség pontosan akkor áll fenn, ha az A,P,D,U pontok ebben a sorrendben egy körön vannak. Hasonlóképpen BV.CP+CV.BP\(\displaystyle \ge\)BC.VP=VP; egyenlőség akkor van, ha B,V,C,P egy körön van. Végül a háromszög-egyenlőtlenség szerint UP+VP\(\displaystyle \ge\)UV.
Az egyenlőtlenségekben szereplő szakaszok hossza: \(\displaystyle AU=CV={1\over2}\), \(\displaystyle DU={3\sqrt5\over10}\), \(\displaystyle BV={\sqrt5\over2}\) és \(\displaystyle UV={3\sqrt{10}\over5}\), tehát
\(\displaystyle {1\over2}\cdot DP+{3\sqrt5\over10}\cdot AP+ {\sqrt5\over2}\cdot CP+{1\over2}\cdot BP\ge UP+VP\ge{3\sqrt{10}\over5}.\)
Ezt az egyenlőtlenséget \(\displaystyle 2\sqrt5\)-tel szorozva éppen a bizonyítandó állítást kapjuk.
Ha P=Q, akkor egyenlőség áll.
A. 303. A nemnegatív x, y
számokra teljesül, hogy x3+y4 x2+y3. Igazoljuk,
hogy
x2+y3. Igazoljuk,
hogy
x3+y3 2.
2.
Megoldás.
2-x3-y3=3(x2+y3-x3-y4)+(x-1)2(2x+1)+(y-1)2(3y2+2y+1)\(\displaystyle \ge\)0.
A. 304. Melyek azok az R+\(\displaystyle \mapsto\)R+ függvények, amelyekre
f(x+y)+f(x).f(y)=f(xy)+f(x)+f(y)?
Megoldás. Behelyettesítve az x=y=2 értékeket, f(4)+f(2)2=f(4)+2f(2). Ebből azt kapjuk, hogy f(2)=0.
Az x=y=1 helyettesítésből f(2)+f2(1)=3f(1), azaz f2(1)-3f(1)+2=0. Ez egy másodfokú egyenlet f(1)-re, amelynek két megoldása van: az 1 és a 2.
1. eset: f(1)=1. Megmutatjuk, hogy ebben az esetben az f függvény egyszerre additív és multiplikatív, azaz tetszőleges u,v számok esetén f(u+v)=f(u)+f(v) és f(uv)=f(u)f(v). Az (1) függvényegyenlet alapján elég az egyiket, mondjuk az additív tulajdonságot igazolni.
A függvényegyenletbe y=1-et helyettesítve, f(x+1)+f(x).f(1)=2f(x)+f(1), azaz tetszőleges pozitív x esetén f(x+1)=f(x)+1.
Legyen most u és v két tetszőleges pozitív szám. Az (1) egyenletet írjuk fel az x=u, y=v/u és az x=u, y=v/u+1 számpárokra is:
f(u+v/u)+f(u).f(v/u)=f(v)+f(u)+f(v/u),
illetve
f(u+v/u+1)+f(u).f(v/u+1)=f(u.(v/u+1))+f(u)+f(v/u+1),
f(u+v/u)+1+f(u)(f(v/u)+1)=f(u+v)+f(u)+f(v/u)+1.
A két egyenletet kivonva egymásból, f(u+v)=f(u)+f(v).
Az additivitásból következik, hogy tetszőleges n pozitív egészre f(n)=n. A multiplikativitásból pedig tetszőleges k,n egészek esetén f(k/n)=f(k)/f(n)=k/n. Tehát tetszőleges q pozitív racionális számra f(q)=q. Az additivitásból következik, hogy a függvény monoton: x<y esetén f(x)<f(x)+f(y-x)=f(y).
Az egyetlen ilyen függvény az identitás: f(x)=x.
2. eset: f(1)=2. Megmutatjuk, hogy a függvény konstans: tetszőleges u pozitív valós számra f(u)=2.
Ismét y=1-et helyettesítve a függvényegyenletbe, f(x+1)+2f(x)=2f(x)+2, tehát f(x+1)=2. Ezzel állításunkat máris igazoltuk u>1-re.
Legyen most u egy tetszőleges valós szám. Válasszunk egy olyan v értéket, amelyre v, uv és u+v is nagyobb mint 1. A függvényegyenlet szerint f(u+v)+f(u).f(v)=f(uv)+f(u)+f(v), azaz 2+f(u).2=2+f(u)+2, tehát f(u)=2.
A függvényegyenletnek tehát két megoldása van: f(x)=x, illetve f(x)=2.

