A 2002. decemberi C-jelű matematika gyakorlatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

C. 695. Egy hatjegyű számot csökkentünk a számjegyeinek összegével, majd az így kapott számmal ugyanezt folytatjuk. Eljuthatunk-e így a 2002-höz?

Megoldás. Egy szám és a számjegyeinek az összege kilenccel osztva ugyanazt a maradékot adja, vagyis különbségük osztható kilenccel. Mivel a 2002 nem osztható kilenccel, ezért nem kaphatjuk meg a feladatban leírt módon.

C. 696. Oldjuk meg az |x+3|+p|x-2|=5 egyenletet, ahol a p valós paraméter.

Megoldás. Három esetet vizsgálunk. Az egyes estekben rendezés után a következő egyenleteket kapjuk: 1. Ha 2$\displaystyle le$x, akkor (p+1)x=2(p+1). 2. Ha -3$\displaystyle le$x$\displaystyle le$2, akkor (1-p)x=2(1-p). 3. Ha x$\displaystyle le$-3, akkor (p+1)x=2(p-4).

A megoldások tehát: Ha p$\displaystyle ne$ $pm$ 1, akkor x=2 az 1. és a 2. esetből adódóan, a 3. esetben pedig figyelembe véve az x=2(p-4)/(p+1) $le$ -3 feltételt, kapjuk, hogy -1<p $le$ 1 esetén x=2(p-4)/(p+1) is megoldás. Ha p=-1, akkor az 1. esetből 2 $le$ x tetszőleges, ha pedig p=1, akkor a 2. esetből -3 $le$ x $le$ 2 tetszőleges.

C. 697. Az ABCD négyszögben AB=1, BC=2, 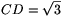$CD=\sqrt{3}$ , ABC $\angle$ =120^o, végül BCD $\angle$ =90^o. Mekkora az AD oldal hosszának pontos értéke?

Megoldás.

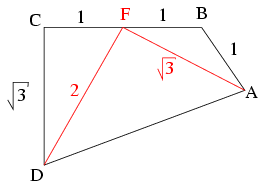
Legyen a BC oldal felezőpontja F. Ekkor azABF háromszög egyenlő szárú, ezért BFA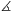 $mangle$ =30^o és 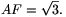$AF=\sqrt{3}.$ Az FCD derékszögű háromszög egyik befogója FC=1, a másik pedig 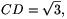$CD=\sqrt{3},$ ezért átfogója FD=2 és DFC 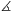$mangle$ =60^o. Vagyis az AFD háromszögben D-nél derékszög van, ezért Pitagorasz tétele szerint AD²=AF²+FD²=3+4, tehát a négyszög AD oldalának hossza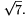 $\sqrt{7}.$

C. 698. Egy háromszögben az AB oldal hossza 10 cm, az AC oldal hossza 5,1 cm, CAB $\angle$ =58^o. Határozzuk meg a BCA $\angle$ -et 1 századfok pontossággal.

Megoldás. A koszinusztétel szerint

BC²=AC²+AB²-2AB^.ACcos58^o=26,01+100-54,0518,

tehát BC=8,4828 cm.

A BCA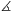 $mangle$ -et ugyancsak a koszinusztétel segítségével határozhatjuk meg:

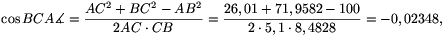
$\cos BCA\measuredangle=\frac{AC^2+BC^2-AB^2}{2AC\cdot CB}=\frac{26,01+71,9582-100}{2\cdot5,1\cdot8,4828}=-0,02348,$

vagyis BCA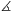 $mangle$ =91,3456^o.

C. 699. Mennyi a valószínűsége annak, hogy az 5-ös lottó sorsolásakor legalább egy olyan számot is kihúznak, amely az előző heti nyertes számok között szerepelt?

Megpldás. Annak a valószínűsége, hogy az előző heti nyerőszámok közül egyetlen egyet sem húznak ki, 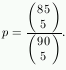. Az általunk keresett valószínűség pedig 1-p=0,2537.

Már regisztráltál?
Új vendég vagy?