Fizikából kitűzött gyakorlatok és feladatok
2002. december

Kérjük, olvassa el a versenykiírást.

Mérési feladat

M. 238. Függőlegesen álló, leszűkített nyílású tölcsért - miközben nyílását alul befogjuk, - töltsünk tele vízzel. Ezután a nyílást szabaddá téve hagyjuk a vizet kifolyni. Mérjük a vízszint helyzetét az idő függvényében! Hogyan változik a vízszint süllyedésének sebessége? (6 pont)

Szilva Attila (Miskolc) ötlete alapján

Az elméleti versenyben kitűzött gyakorlatok és feladatok Az elméleti fizika feladatokra kapható pontszám a feladatok nehézségétől függ. Az 1-8. osztályosok versenyében minden hónapban a 3 legnagyobb, a 9-12. osztályosok versenyeiben minden hónapban az 5 legnagyobb pontszám számít be a pontversenybe.

P. 3571. Belül üres fémkocka külső élhosszúsága 5 mm, falvastagsága 1 mm. A fém sűrűsége 8400 kg/m³. Mi történik a kockával, ha a víz felszíne alatt tartjuk, majd elengedjük? (3 pont)

Komárom-Esztergom megyei ,,Ifjú Fizikus'' verseny nyomán

P. 3572. Bizonyos mennyiségű ideális gáz az ábrán látható körfolyamatot végzi. Mennyi a gáz által végzett munka egy ciklus során?

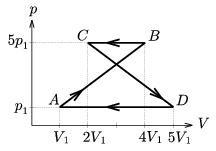
(3 pont)

Közli: Veres Zoltán, Margitta

P. 3573. Mekkora munka árán tudunk becsapni egy tömör fából készült, 24 kg tömegű ajtót úgy, hogy a széle 5 m/s sebességgel csapódjon az ajtótoknak? (4 pont)

Közli: Holics László, Budapest

P. 3574. Mennyi hő elvonásával készíthető 2 kg -5 ^oC hőmérsékletű túlhűtött vízből ugyanilyen hőmérsékletű jég? (4 pont)

Közli: Pálfalvi László, Pécs

P. 3575. M tömegű szánkón m tömegű kutya áll, amely u relatív sebességgel tud leugrani a szánkóról, majd v sebességgel tud utána szaladni és felugrani rá.

Elhanyagolva a szánkó súrlódását a hóborította vízszintes talajon, határozzuk meg, hogy végül is mekkora sebességre gyorsulhat fel így a szánkó és a kutya! Hányszor ugrik fel közben a kutya a szánkóra?

Legyen M=30 kg, m=10 kg, u=0,5 m/s, v=4 m/s. (5 pont)

Közli: Varga István, Békéscsaba

P. 3576. Rögzített, =30^o-os hajlásszögű lejtőre egy m tömegű tömör hengert helyezünk. A hengert a palástjára csavart fonál segítségével a lejtőre merőlegesen F=x^.mg nagyságú erővel húzzuk. A henger csúszásmentesen gördül a lejtőn.

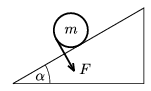
a) Határozzuk meg és ábrázoljuk a tapadási súrlódási erőt x függvényében!

b) Mekkorának kell választani x értékét, ha a lejtő felülete nagyon sima?

c) Legalább mekkorának kell lennie a tapadási súrlódási együtthatónak, ha a henger középpontja 2g gyorsulással mozog? (5 pont)

Közli: Kotek László, Pécs

P. 3577. Határozzuk meg egy téglalap keresztmetszetű toroid induktivitását! A tekercs menetszáma N, középkörének sugara R, a téglalap oldalai a és b. (Az a hosszúságú oldal párhuzamos a toroid tengelyével.)

Adatok: N=1000, R=10 cm, a=6 cm, b=4 cm. (5 pont)

Közli: Simon Péter, Pécs

P. 3578. Egy felhő 0,1 mm átmérőjű vízcseppjei 10 V-ra töltődnek fel. A kicsiny cseppek 2,7 mm átmérőjű nagy cseppekké egyesülnek.

Mekkora lesz ezeknek a feszültsége? (4 pont)

Nagy László (1931-1987) feladata nyomán

P. 3579. Ugyanakkora gyorsítófeszültség hatására hányszor nagyobb sebességre gyorsul fel vákuumban egy proton, mint egy \(\displaystyle \alpha\)-részecske, ha kezdeti sebességük elhanyagolható? (4 pont)

Közli: Radnai Gyula, Budapest

P. 3580. Egy űrállomás R=10 m sugarú forgó henger alakú tornatermében a földi g-nek megfelelő nagyságú ,,mesterséges gravitációt'' hoznak létre. Amikor nem használják a tornatermet, (rosszul értelmezett takarékosságból) egyenletes lassítással g-t a szokásos érték felére csökkentik.

Mennyi időre van szükség a lassításhoz, ha azt akarják, hogy a padlón lévő szőnyegek ne csússzanak el eredeti helyükről? (A tapadási súrlódási együttható a szőnyegek és a padló között legalább 0,1.) (4 pont)

Mennyire csökkenthető le a fékezés ideje, ha nem ragaszkodunk az egyenletes lassításhoz? Mennyi időre lenne szükség a teljes súlytalanság eléréséhez? (+2 pont)

Közli: Szokoly Gyula, Németország

Pontversenyen kívüli feladat. (A megoldás beküldhető, a dolgozatokat értékeljük, a legszebb megoldást közöljük, de az eredmény nem számít be a pontversenybe.) Egy szilveszteri bulin a társaság arról vitatkozik, hogy a pezsgőspohárban hogyan mozognak a felszálló buborékok: egyenletesen vagy gyorsulva, esetleg lassulva. Neked mi a véleményed?

A fizika feladatok megoldásai a következő címekre küldhetők:

KöMaL Szerkesztőség
Budapest 112, Pf. 32.  1518

megoldas@komal.hu (Az interneten keresztül történő beküldésről olvassa el tájékoztatónkat)

A beküldési határidő: 2003. január 11.