 |
Exercises and problems in Informatics |
Please read The Conditions of the Problem Solving Competition.
I. 37. Write your program (I37.pas,
...) which converts a fixed point real number (having at most
100 digits both in front of and behind its decimal point) from
base A (2\(\displaystyle \le\)A \(\displaystyle \le\)100) to a number in base B (2
B 100). (10 points)
I. 38. Given a line segment (x1,y1,x2,y2), we perform a series of transformations to obtain various planar figures.
In the simplest case, the line segment is translated (with real parameters dx and dy), during which its endpoints are drawn continuously.
Example 1. Three translations with (dx,dy)=(50,0), (20,30) and (40,10), respectively, applied to the line segment (100,100,100,200).
Besides translations, we can also apply similarities at the same time (from the endpoint of the first line segment and of scale factor s). The first two parameters of this operation correspond to the translation component, while the third parameter s is the scale factor.
Example 2. Three compound operations with (dx,dy,s)=(50,-50,2), (100,0,1) and (50,0,0.75), respectively, are applied to the line segment (100,100,100,200).
Finally, the third simultaneously performed operation is rotation. Its two parameters are the centre of rotation t (representing multiples of the length of the line segment from its first endpoint to the centre possibly along the extension of the segment) and the angle of rotation f (given in degrees counterclockwise).
Example 3. Two compound operations with (dx,dy,s,t,f) = (0,0,1,0,60) and (0,0,1,1,-120), respectively, applied to the line segment (100,100,100,200).
When the centre of rotation is outside the line segment, the result might be spectacular, indeed. For example, apply the operation (0,0,1,-1,180) to the segment (100,150,100,200). Another peculiar figure is obtained by applying two operations, (50,0,1,-0.5,60) and (25,25,2,1.5,-90) to the line segment (100,100,100,200).
Write your program (I38.pas, ...) which reads the endpoints of the line segment and the parameters of N consecutive operations and displays the corresponding figure. (10 points)
 |  |  |  |  |
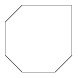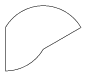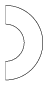| Example 1 | Example 2 | Example 3 | Example 4 | Example 5 |
I. 39. Nonnegative rational numbers can
uniquely be written as \(\displaystyle A\frac{b}{c}\), where A
0, b 0, c>0,
b<c, further b and c are relatively
prime. Moreover, if A=0 or b=0, then the number should
be represented as \(\displaystyle \frac{b}{c}\) or A, respectively. Prepare your sheet
(I39.xls) which displays the sum if the two addends are entered.
Examples:
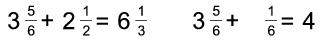
(10 points)