New exercises and problems in Mathematics
December 2002

Please read The Conditions of the Problem Solving Competition.

New exercises

Maximum score for each exercise (sign "C") is 5 points.

C. 695. We decreased a six-digit number by the sum of its digits, and went on repeating same procedure with the resulting number. Is it possible that we obtained 2002 in this way?

C. 696. Solve the equation |x+3|+p|x-2|=5, where p is a real parameter.

C. 697. In the quadrilateral ABCD,

AB=1, BC=2, 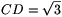$CD=\sqrt3$ , ABC$\displaystyle \angle$=120^o, and BCD $\angle$ =90^o.

Find the exact value of the length of side AD.

C. 698. The length of side AB in a triangle is 10 cm, the length of side AC is 5,1 cm, and CAB$\displaystyle \angle$=58^o. Determine the measure of BCA$\displaystyle \angle$ to the nearest hundredth of a degree.

C. 699. What is the probability that at least one of the five numbers drawn (out of 1 to 90) in a lottery was also drawn last week? (There is one lottery draw per week.)

New problems

The maximum scores for problems (sign "B") depend on the difficulty. It is allowed to send solutions for any number of problems, but your score will be computed from the 6 largest score in each month.

B. 3592. Santa Claus was watching the sky anxiously, deep in contemplation. He wanted to travel as far away as possible the day after to deliver gifts to children. Finally, at midnight it started snowing. Being an expert on snowfall he saw immediately that it was the kind of snow that would not stop falling for at least 24 hours. He also knew that during the first 16 hours the sleigh can travel faster and faster. (The speed can be increased uniformly.) It would be standing still at the beginning but by the end of the 16-th hour it would be flying like an arrow. Then, however, it would be harder and harder to travel in the thickening snow, and during the remaining 8 hours the top speed would be uniformly decreasing back to zero. Santa Claus, on the other hand did not want to exhaust his reindeer by forcing them for more than 8 hours. When should he depart in order to cover the greatest distance possible? (4 points)

B. 3593. Is there an arithmetic progression of different positive integers in which no term is divisible by any square number greater than 1? (3 points)

B. 3594. Is there a square number in decimal notation in which the sum of the digits is 2002? (4 points)

B. 3595. Solve the following equation:

2x⁴+2y⁴-4x³y+6x²y²-4xy³+7y²+7z²-14yz-70y+70z+175=0.

(3 points) (Suggested by M. Haragos and M. Zsoldos, Budapest)

B. 3596. The circle k₁ of radius R touches the circle k₂ of radius 2R externally at the point E₃, and the circles k₁ and k₂ are also touched from the outside by the circle k₃ of radius 3R. The circles k₂ and k₃ touch at the point E₁, and the circles k₃ and k₁ at the point E₂. Prove that the circumcircle of the triangle E₁E₂E₃ is congruent to the circle k₁. (3 points) (Suggested by B. Bíró, Eger)

B. 3597. Is it true that if there exists a line parallel to the bases of a given trapezium that halves both its area and its perimeter then the trapezium is a parallelogram? (4 points)

B. 3598. Isosceles triangles with apex angles of 140^o are drawn over the sides AB and BC of a given triangle ABC (on the outside). The new vertices obtained are A₁ and C₁. Then an isosceles tiangle of apex angle 80^o is drawn over the side AC (outside). Determine C₁B₁A₁ $\angle$ ? (4 points)

B. 3599. A right truncated cone is circumscribed about a sphere. What is the maximum possible ratio of the volume of the truncated cone to its surface area? (4 points)

B. 3600. Find a cube in the 3D cartesian system whose edges are not parallel to the coordinate axes but have an integer length. (5 points)

B. 3601. Ann and Sophie take turns rolling a die. The number shown by the die is always added to their respective scores. Whoever obtains the first score divisible by 4, wins the game. Given that Anna starts the game, what is the probability that she will win? (5 points)

New advanced problems

Maximum score for each advanced problem (sign "A") is 5 points.

A. 305. Prove that if n is an arbitrary positive integer then

$\displaystyle \sum_{\textstyle{k_1,\dots,k_n\geq0\atop k_1+2k_2+\dots+nk_n=n}} \frac{(k_1+k_2+\dots+k_n)!}{k_1!\cdot\ldots\cdot k_n!}=2^{n-1}.$

A. 306. The orthocentre of the triangle ABC is M, and its incircle, centred at O, touches the sides AC and BC at the points P and Q. Prove that if M lies on the line PQ then the line MO passes through the midpoint of the side AB.

A. 307. Let a_n denote the coefficient of xⁿ in the polynomial (x²+x+1)ⁿ. Prove that if p>3 is a prime number then

a_p $\equiv$ 1 (mod p²).

Send your solutions to the following address:

or by e-mail to:

solutions@komal.hu

Already signed up?
New to KöMaL?