A 2003. januári B-jelű matematika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

B.3602.A négyzet alakú medencében úszkáló Jerry el szeretne menekülni a parton rá leső Tom elől. Tom nem tud úszni, lassabban fut, mint Jerry, viszont négyszer olyan gyorsan fut, mint ahogy Jerry úszik. Megmenekülhet-e mindig Jerry?

(5 pont)

Megoldás:Jerry mindig megmenekülhet, ha a következő stratégiát követi. Tegyük fel, hogy a medence kerülete egy egység oldalú O középpontú n négyzet és jelölje n' azt a négyzetet, amelynek oldalai n oldalaival párhuzamosak, középpontja O, oldalhossza pedig egy 1/5 és 1/4 közé eső d szám, mondjuk d=0,22.

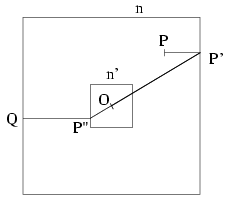
Ha P jelöli Tom pillanatnyi helyzetét, P' az n négyzet P-hez legközelebb lévő pontját, P'' pedig az n' négyzet P'-vel átellenben lévő pontját, akkor Tom mozgása során a P' pont pillanatnyi sebessége nem lehet nagyobb Tom sebességénél, a P'' pont sebessége pedig ennek d-szerese, vagyis nem nagyobb, mint Jerry úszási sebességének 4d-szerese. Ezért ha Jerry először is ráúszik a képzeletbeli n' négyzet kerületére, majd annak mentén Tom mozgását követve úgy úszkál, hogy a megfelelő P'' ponthoz mindig közeledjék, akkor előbb-utóbb Tommal átellenben fog elhelyezkedni az n' négyzet kerületén.

Ha ekkor elkezd egyenes vonalban úszni a medence hozzá legközelebb lévő Q pontjához, akkor biztosan megmenekül, ugyanis ekkor neki (1-d)/2 utat kell megtennie, míg Tomnak, amint azt mindjárt kiszámoljuk, legalább (3+d)/2 utat kell megtennie, ami a d>1/5 választás miatt meghaladja Jerry útjának 4-szeresét.

Valóban, ha Tom el szeretne jutni a Q pontba, akkor mozgása során legalább akkora utat meg kell tennie, mint a neki megfelelő P' pontnak az n négyzet kerületén. Ha kezdetben ez valamelyik csúcstól x$\displaystyle \le$1/2 távolságra van, akkor a P' és Q pontok távolsága az n négyzet mentén

$\displaystyle \min\Bigl\{x+1+{1\over2}+{d\over2}-xd\ ,\ (1-x)+1+{1-d\over2}+xd\Bigr\}\ge{3+d\over2}\ .$

B.3603. Szerkesszünk adott háromszög belsejében olyan pontot, melynek a háromszög oldalegyeneseitől való távolságainak aránya 1:2:3.

(3 pont)

Megoldás: Legyenek a háromszög csúcsai A,B,C, és vegyünk fel egy viszonylag kicsi k távolságot. Legyen D az a pont az ABC szögtartomány belsejében, melynek BC egyenestől való távolsága k, AB egyenestől vett távolsága pedig 3k. Azon pontok mértani helye az ABC szögtartományban, melyeknek a háromszög a és c oldalaitól vett távolságainak aránya 1:3, éppen a B-ből induló, D-n áthaladó nyílt félegyenes. Hasonlóképpen, azon pontok mértani helye az ACB szögtartományban, melyeknek a háromszög a és b oldalaitól vett távolságainak aránya 1:2, éppen a C-ből induló, E-n áthaladó nyílt félegyenes, ahol E azon pontja az ACB szögtartománynak, melynek az AC egyenestől vett távolsága 2k, míg a BC egyenestől vett távolsága k. Miként a D,E pontok, e két félegyenes is könnyen megszerkeszthetők, és metszéspontjuk, mely nyilván a háromszög belsejébe esik, lesz az a pont, melynek az a,b és c oldalaktól vett távolságainak aránya éppen 1:2:3.

Hasonlóképpen megszerkeszthetjük azt a pontot is, melynek a b,a és c oldalaktól vett távolságainak aránya lesz a kívánt 1:2:3 aránnyal egyenlő. Világos, hogy a háromszög oldalainak bármely permutációjához tartozik ilyeténképpen egy megoldás, és könnyű meggondolni, hogy mind a 6 permutációhoz különböző megoldás fog tartozni.

B.3604. Az x, y valós számokra teljesül, hogy x+y=1. Határozzuk meg az A(x,y)=x⁴y+ xy⁴+ x³y+ xy³+ x²y+ xy² kifejezés legnagyobb értékét.

(3 pont)

Megoldás: A t=xy jelölést bevezetve x²+y²=(x+y)²-2xy=1-2t és x³+y³=(x+y)(x²-xy+y²)=1-3t. Ezért

$\displaystyle A(x,y)=t(x^3+y^3+x^2+y^2+x+y)=t(3-5t)={5t(3-5t)\over5}.$

Ez a t-ben másodfokú kifejezés legnagyobb értékét a t=3/10 helyen veszi fel, a ]-$\displaystyle infty$,3/10] intervallumban pedig szigorúan monoton növekedő.

Az x+y=1 feltétel miatt t lehetséges legnagyobb értéke 1/4, amit x=y=1/2 esetén vesz fel. Mivel 1/4<3/10, megállapíthatjuk, hogy az A(x,y) kifejezés legnagyobb értéke

A(1/2,1/2)=(1/4)(3-5/4)=7/16.

B.3605. Az ABC háromszög CA oldalának A-n túli meghosszabbításán adott a D pont, a CB oldalának B-n túli meghosszabbításán pedig az E pont úgy, hogy AB=AD=BE. Az ABC háromszög A-ból és B-ből induló szögfelezői a szemközti oldalakat az A₁ illetve a B₁ pontokban metszik. Mekkora az ABC háromszög területe, ha a DCE háromszög területe 9 egység, az A₁CB₁ háromszög területe pedig 4 egység?

(3 pont)

Javasolta: Bakonyi Gábor, Budapest

Megoldás: A szokásos jelölésekkel élve, az ABC háromszög területe t=$\displaystyle kappa$ab, ahol $\displaystyle kappa$=(1/2)sin$\displaystyle gamma$. Mivel CD=b+c és CE=a+c, a DCE háromszög területe t₁=$\displaystyle kappa$(a+c)(b+c). Végül a szögfelező tétel alapján CA₁=ab/(b+c) és CB₁=ba/(a+c), vagyis az A₁CB₁ háromszög területe t₂=$\displaystyle kappa$(ab)²/(a+c)(b+c). Innen leolvasható, hogy t²=t₁t₂, vagyis $\displaystyle t=\sqrt{9\cdot4}=6$.

B.3606. Adjunk meg olyan a és b egész számokat, amelyekre teljesül, hogy 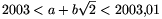$2003<a+b\sqrt2<2003{,}01$ .

(3 pont)

Megoldás: Induljunk ki abból, hogy $\displaystyle 0<\sqrt{2}-1<1/2$, innen

$\displaystyle 0<3-2\sqrt{2}=(\sqrt{2}-1)^2<1/4,$

$\displaystyle 0<17-12\sqrt{2}=(3-2\sqrt{2})^2<1/16<1/10,$

$\displaystyle 0<577-408\sqrt{2}=(17-12\sqrt{2})^2<1/100,$

ahonnan $\displaystyle 2003<2580-408\sqrt{2}<2003,01$. Az a=2580, b=-408 választás tehát megfelelő lesz.

B.3607. Egy konvex négyszög szemközti oldalegyenesei metszik egymást. Megrajzoljuk a metszéspontoknál keletkezett szögek belső szögfelezőit. Bizonyítsuk be, hogy a négyszög akkor és csak akkor húrnégyszög, ha e két szögfelező merőleges egymásra, és ebben az esetben a szögfelezők a négyszög oldalait egy rombusz csúcsaiban metszik.

(4 pont)

Javasolta: Rácz János, Budapest

Megoldás:

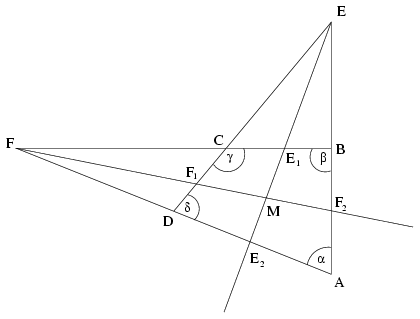
Legyen az ABCD négyszögben az AB és DC félegyenesek metszéspontja E, az AD és BC félegyenesek metszéspontja pedig F. Az AED szög e szögfelezője messe a BC és AD oldalakat rendre az E₁,E₂ pontokban, az AFB szög f szögfelezője pedig messe a CD és AB oldalakat rendre az F₁,F₂ pontokban. Végül jelölje e és f metszéspontját M. A négyszög A,B,C és D csúcsainál lévő szögeket rendre $\displaystyle alpha$,$\displaystyle beta$,$\displaystyle gamma$, illetve $\displaystyle delta$-val jelölve kiszámolhatjuk, hogy az AEE₂ szög nagysága (180^o-$\displaystyle alpha$-$\displaystyle beta$)/2, ahonnan az AE₂E szög nagyságára 90^o-$\displaystyle alpha$/2+$\displaystyle delta$/2 adódik. Ugyanígy kapjuk, hogy az AF₂F szög 90^o-$\displaystyle alpha$/2+$\displaystyle beta$/2, ahonnan az E₂MF₂ szögre 180^o-$\displaystyle beta$/2-$\displaystyle delta$/2 adódik. Tehát e pontosan akkor merőleges f-re, ha $\displaystyle beta$+$\displaystyle delta$=180^o, vagyis ha az ABCD négyszög húrnégyszög.

Ebben az esetben az E₁FE₂ háromszögben az F-ből induló e szögfelező merőleges az E₁E₂ oldalra, amiért is a háromszög egyenlő szárú, FE₁=FE₂. Emiatt az E₂FF₁ és E₁FF₁ háromszögek egybevágóak, tehát E₂F₁=F₁E₁. Ugyanígy kapjuk azt is, hogy F₁E₁=E₁F₂. Az E₁F₁E₂F₂ négyszögben tehát az egymásra merőleges átlók egyenese egyben szimmetriatengely is, a négyszög valóban egy rombusz.

B.3608. Adjuk meg azoknak az a, b, c számoknak a tízes számrendszerbeli alakját, amelyekre az x³+ax²+bx+c=0 egyenlet gyökei rendre egyenlők az x³-3x+1=0 egyenlet három gyökének az ötödik hatványával.

(4 pont)

Megoldás: Ha f(x)=x³-3x+1, akkor f(-2)<0, f(0)>0, f(1)<0 és f(2)>0 miatt az f(x)=0 egyenletnek 3 különböző valós gyöke van. Ha ezek x₁,x₂,x₃ akkor

s=x₁+x₂+x₃=0,

t=x₁x₂+x₁x₃+x₂x₃=-3

és

p=x₁x₂x₃=-1,

a gyökök és együtthatók közötti összefüggések alapján. Innen rögtön leolvasható, hogy

c=-x₁⁵x₂⁵x₃⁵=-p⁵=1.

Ismeretes, hogy s,t és p segítségével előállí tható minden olyan kifejezés, amely x₁,x₂,x₃-ban szimmetrikus. Kezdve az egyszerűbbekkel,

u=x₁²+x₂²+x₃²=s²-2t=6

és

v=x₁²x₂+x₁²x₃+x₂²x₁+x₂²x₃+x₃²x₁+x₃²x₂=st-3p=3,

ahonnan

w=x₁³+x₂³+x₃³=su-v=-3.

Továbbá

y=x₁²x₂²+x₁²x₃²+x₂²x₃²=t²-2ps=9,

z=x₁³x₂²+x₁³x₃²+x₂³x₁²+x₂³x₃²+x₃³x₁²+x₃³x₂²=sy-pt=-3,

ahonnan

q=x₁⁵+x₂⁵+x₃⁵=uw-z=-15.

Végül

r=x₁³x₂+x₁³x₃+x₂³x₁+x₂³x₃+x₃³x₁+x₃³x₂=tu-ps=-18,

m=x₁³x₂³+x₁³x₃³+x₂³x₃³=ty-pv=-24,

és így

n=x₁⁵x₂⁵+x₁⁵x₃⁵+x₂⁵x₃⁵=ym-p²r=-198.

Az egyenlet együtthatói tehát a=-q=15, b=n=-198 és c=1.

B.3609. Van-e olyan f(x) egész együtthatós 2003-ad fokú polinom, amelyre bármely n egész szám esetén az

f(n), f(f(n)), f(f(f(n))), ...

értékek páronként relatív prímek?

(5 pont)

Megoldás: Legyen f₁(x)=f(x) és f_k+1(x)=f(f_k(x)), ha k$\displaystyle ge$1 egész szám. Mivel f_k+l(x)=f_l(f_k(x)), elegendő lenne azt biztosítani, hogy minden n egész számra n relatív prím az f_k(n) számok (k=1,2,...) mindegyikéhez. Ez pedig nyilván teljesül, ha minden k-ra f_k(x)=x^.g_k(x)+1 valamilyen alkalmas g_k(x) egész együtthatós polinommal.

Azt állítjuk, hogy ez teljesül, ha például f(x)=x²⁰⁰³-x+1. Valóban, k=1 esetén g₁(x)=x²⁰⁰²-1 megfelelő lesz. Ha pedig valamely k pozitív egészre a g_k(x) polinomot már megtaláltuk, akkor

f_k+1(x)=f(xg_k(x)+1)=(xg_k(x)+1)²⁰⁰³-(xg_k(x)+1)+1

$\displaystyle =\sum_{i=2}^{2003}{2003\choose i}x^i(g_k(x))^{i}+2002xg_k(x)+1,$

ahonnan leolvasható, hogy a

$\displaystyle g_{k+1}(x)=\sum_{i=2}^{2003}x^{i-1}(g_k(x))^{i}+2002g_k(x)$

egész együtthatós polinom megfelelő lesz.

Az f(x)=x²⁰⁰³-x+1 polinom tehát megoldása a feladatnak.

B.3610. Bizonyítsuk be, hogy

sin 25^o^.sin 35^o^.sin 60^o^.sin 85^o=sin 20^o^.sin 40^o^.sin 75^o^.sin 80^o.

(5 pont)

Megoldás: A sin(90^o-$\displaystyle alpha$)=cos$\displaystyle alpha$=-cos(180^o-$\displaystyle alpha$) és 2cos$\displaystyle alpha$cos$\displaystyle beta$=cos($\displaystyle alpha$-$\displaystyle beta$)+cos($\displaystyle alpha$+$\displaystyle beta$) összefüggésekre támaszkodva

8(sin25^osin35^osin60^osin85^o-sin20^osin40^osin75^osin80^o)=

=8(cos65^ocos55^ocos30^ocos5^o-cos70^ocos50^ocos15^ocos10^o)=

=2(cos10^o+cos120^o)(cos25^o+cos35^o)-

-2(cos20^o+cos120^o)(cos5^o+cos25^o)=

=2cos10^ocos25^o+2cos10^ocos35^o+2cos120^ocos35^o-

-2cos20^ocos5^o-2cos20^ocos25^o-2cos120^ocos5^o=

=cos15^o+cos35^o+cos25^o+cos45^o+cos85^o+cos155^o-

-cos15^o-cos25^o-cos5^o-cos45^o-cos115^o-cos125^o=

=cos35^o+cos85^o-cos25^o-cos5^o+cos65^o+cos55^o=

=2cos60^ocos25^o-cos25^o-cos5^o+2cos60^ocos5^o=0,

hiszen 2cos60^o=1. Ez bizonyítja az állítást.

B.3611. Az x_n+1=x_n²-x_n+1 rekurzióval definiált sorozat elemeiből készítsük el a 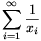$\sum_{i=1}^{\infty}\frac{1}{x_i}$ végtelen sort. Mennyi ennek a sornak az összege, ha a) x₁=1/2; b) x₁=2?

(5 pont)

Megoldás: Ha 0<x<1, akkor 0<1-x<x²-x+1=1-x(1-x)<1. Ha tehát x₁=1/2, akkor a sorozat minden eleme 0 és 1 közé esik, ezért minden n-re 1/x_n>1, vagyis a végtelen sor összege $\displaystyle infty$.

Ha azonban x$\displaystyle ge$2, akkor x²-x+1=x+1+x(x-2)$\displaystyle ge$x+1. Ezért x₁=2 esetén az x_n sorozat szigorúan monoton növekedően végtelenhez tart, az 1/x_n sorozat pedig szigorúan monoton csökkenő módon 0-hoz tart. Továbbá az $\displaystyle s_n=\sum_{i=1}^n{1\over x_i}$ sorozatot tekintve teljes indukcióval könnyen ellenőrizhető, hogy minden n pozitív egészre $\displaystyle s_n=1-{1\over x_n(x_n-1)}$. Valóban, n=1 esetén ez igaz, ha pedig valamely n-re teljesül, akkor lévén

$\displaystyle s_{n+1}=s_n+{1\over x_{n+1}}=1-{1\over x_{n+1}-1}+{1\over x_{n+1}}=1-{1\over x_{n+1}(x_{n+1}-1)},$

az állítás n+1-re is teljesül. Ebből következik, hogy

$\displaystyle 1-{1\over x_n}\le1-{1\over x_n(x_n-1)}=s_n<1.$

Az s_n sorozat tehát 1-hez tart, ami azt jelenti, hogy a végtelen sor összege ebben az esetben 1.

Már regisztráltál?
Új vendég vagy?