Fizikából kitűzött gyakorlatok és feladatok
2003. január

Kérjük, olvassa el a versenykiírást.

Mérési feladat

M. 239. Háztartási alufóliából vágjunk ki R+h sugarú körlapot, majd ezt simítsuk rá egy R sugarú hengerre úgy, hogy leszedve egy h magasságú tálkát kapjunk. Különböző R értékeket választva (R+h állandó) mérjük meg, hogyan függ a tálka állandósult v₀ esési sebessége R-től! Határozzuk meg, hogyan függ a közegellenállás formatényezője az R/h aránytól!

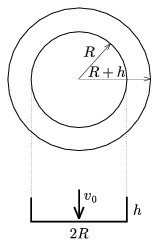
(6 pont)

Közli: Varga István, Békéscsaba

Az elméleti versenyben kitűzött gyakorlatok és feladatok Az elméleti fizika feladatokra kapható pontszám a feladatok nehézségétől függ. Az 1-8. osztályosok versenyében minden hónapban a 3 legnagyobb, a 9-12. osztályosok versenyeiben minden hónapban az 5 legnagyobb pontszám számít be a pontversenybe.

P. 3581. A világ egyik legnagyobb gyémántja 44,5 karátos, csaknem tiszta szén. Hány szénatom van ebben az óriás kristályban?

(3 pont)

Közli: Radnóti Katalin, Budapest

P. 3582. Légpárnás asztalon három egyforma korong van, tömegeloszlásuk egyenletes. Két korong érintkezik egymással, ezek nem mozognak. A harmadik korong feléjük tart, sebessége merőleges a két álló korong középpontját összekötő egyenesre. Adjuk meg a tökéletesen rugalmas és súrlódásmentes ütközések utáni sebességek arányát az ábrán látható szög függvényében!

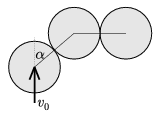
(5 pont)

Közli: Simon Péter, Pécs

P. 3583. Egy R=20 cm sugarú, vízszintes tengelyű, rögzített csőben egy r=6 cm sugarú tömör gömböt kissé kimozdítunk egyensúlyi helyzetéből, majd elengedünk. Mekkora periódusidejű mozgás jön létre, ha a gömb csúszás nélkül gördül a csőben? Legfeljebb mekkora lehet a mozgás amplitúdója, ha a tapadó súrlódás együtthatója \(\displaystyle \mu\)=0,05?

(5 pont)

Közli: Piacsek István, Sopron

P. 3584. Bizonyos mennyiségű héliumgáz állapotváltozását a pV³=állandó formula írja le. A folyamat végére a gáz abszolút hőmérséklete negyedére csökken, belső energiája 1800 J-lal változik. A folyamat során a gáz legkisebb nyomása 10⁵ Pa.

Ábrázoljuk a folyamatot a p-V diagramon a végpontok adatainak feltüntetésével!

(4 pont)

Közli: Kotek László, Pécs

P. 3585. Derékszögben meghajlított, igen nagy kiterjedésű, vékony fémlap mindkét lapjától egyaránt d távolságra elhelyezünk egy m tömegű, Q töltésű kicsiny testet, majd elengedjük.

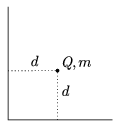
a) Mekkora gyorsulással indul el a test?

b) Mekkora lesz a sebessége, amikor már 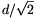utat megtett?

(A gravitáció hatását elhanyagolhatjuk.)

(5 pont)

Közli: Pálfalvi László, Pécs

P. 3586. Egy űrhajóban V térfogatú, T hőmérsékletű, p₀ nyomású levegő van. Az űrhajó falán keletkezik egy A keresztmetszetű piciny lyuk, amelyen keresztül a benti levegő lassan szivárog kifelé.

Mennyi idő alatt csökken a benti levegő nyomása a felére? (Tegyük fel, hogy a benti levegő hőmérséklete nem változik!)

(5 pont)

Közli: Szilva Attila, Miskolc

P. 3587. Függőleges vezető tengelyhez elforgathatóan csatlakozik egy vízszintes fémrúd, amelynek másik vége egy l sugarú vezető körgyűrűre támaszkodik. A gyűrűt az ábra szerint egy R ellenálláson keresztül vezeték köti össze a tengellyel. (Minden más vezető ellenállása és a súrlódás elhanyagolható.)

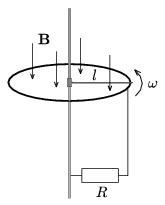
A berendezés homogén, B indukciójú, függőleges mágneses mezőben van. Mekkora erőt kell kifejtenünk a rúd közepénél ahhoz, hogy a rúd állandó \(\displaystyle \omega\) szögsebességgel forogjon?

Adatok: R=0,1 k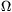, B=0,8 T, l=0,5 m, \(\displaystyle \omega\)=10 s^-1.

(4 pont)

Közli: Holics László, Budapest

P. 3588. U=230 V effektív feszültségű hálózatra sorba kapcsolunk egy 230 ohmos ellenállást, egy ideálisnak tekinthető diódát és egy ampermérőt, amely az áram effektív értékét méri. Mit mutat az ampermérő?

(3 pont)

Közli: Radnai Gyula, Budapest

P. 3589. Függőleges falra kör alakú csengőket erősítettek úgy, hogy minden csengő egy képzeletbeli négyzetrács egy-egy rácspontjába került. Ha a falat 10 mm átmérőjű golyókkal dobáljuk, átlagosan minden negyedik esetben szólal meg valamelyik csengő; ha 30 mm-es golyókkal dobálunk, akkor átlagosan minden második esetben találunk el egy csengőt. Feltételezve, hogy a találatok teljesen véletlenszerűek, határozzuk meg a négyzetrács rácsállandóját és a csengők átmérőjét!

(4 pont)

Közli: Bakonyi Gábor, Budapest

P. 3590. Az ²³⁸U alfa-bomlását további két, egymás utáni béta-bomlás követi. Mekkora az ²³⁸U ,,dédunokájának'' rendszáma és tömegszáma? Mi az elem neve?

(3 pont)

Jay Orear kérdése, Cornell egyetem (USA)

A fizika feladatok megoldásai a következő címekre küldhetők:

KöMaL Szerkesztőség
Budapest 112, Pf. 32.  1518

megoldas@komal.hu (Az interneten keresztül történő beküldésről olvassa el tájékoztatónkat)

A beküldési határidő: 2003. február 11.