New exercises and problems in Mathematics
January 2003

Please read The Conditions of the Problem Solving Competition.

New exercises

Maximum score for each exercise (sign "C") is 5 points.

C. 700. A quadrilateral is cut out of a sheet of paper, and each vertex is folded in so that they meet at a common point. What kind of quadrilateral should that be in order for the folded parts to cover the rest of the quadrilateral without overlap?

C. 701. Show that 1^.2^....^.1001+1002^.1003^....^.2002 is divisible by 2003.

C. 702. The acute angles of a right triangle are 60^o and 30^o. Two circles of the same radius are inscribed in the triangle so that they touch each other, the hypotenuse and one leg each. By what factor is the smaller leg longer than the radius of the circles?

C. 703. Depending on the value of the real parameter p, how many roots does the equation 2x²-10px+7p-1=0 have in the interval (-1;1)?

C. 704. For what natural numbers n is it true that log₂3^.log₃4^.log₄5^....^.log_n(n+1)=10?

New problems

The maximum scores for problems (sign "B") depend on the difficulty. It is allowed to send solutions for any number of problems, but your score will be computed from the 6 largest score in each month.

B. 3602. Jerry is swimming in a square pool. Tom is watching from the edge of the pool and Jerry wants to get away from him. Tom cannot swim at all, cannot run as fast as Jerry but he runs four times as fast as Jerry swims. Can Jerry always escape? (5 points)

B. 3603. In the interior of a given triangle, construct a point such that its ratio of the distances from the lines of the sides are in a 1:2:3 proportion. (3 points)

B. 3604. x, y are real numbers, and x+y=1. Determine the maximum value of the expression

A(x,y)=x⁴y+xy⁴+x³y+xy³+x²y+xy².

(3 points)

B. 3605. Point D lies on the extension of the side CA of a triangle ABC beyond the point A, point E lies on the extension of CB beyond B, and AB=AD=BE. The angle bisectors from A and B intersect the opposite sides at the points A₁ and B₁, respectively. Find the area of the triangle ABC, given that the area of triangle DCE is 9 units and that of triangle A₁CB₁ is 4 units. (3 points) (Suggested by G. Bakonyi, Budapest)

B. 3606. Find suitable integers a and b, such that \(\displaystyle 20034 points)

B. 3607. The lines containing the opposite sides of a convex quadrilateral intersect each other. Draw the interior angle bisectors of the angles formed at the intersections. Prove that the quadrilateral is cyclic if and only if the two angle bisectors are perpendicular to each other, and show that in that case they intersect the sides of the quadrilateral at the vertices of the rhombus. (4 points) (Suggested by J. Rácz, Budapest)

B. 3608. The roots of the equation x³+ax²+bx+c=0 are equal to the fifth powers of the three roots of the equation x³-3x+1=0, respectively. Find the numbers a, b, c in decimal notation. (4 points)

B. 3609. Is there a 2003rd-degree polynomial f(x) of integer coefficients, such that the values of f(n), f(f(n)), 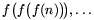$f\big(f\big(f(n)\big)\!\big),\dots$ are pairwise relative primes for every integer n? (4 points)

B. 3610. Prove that

sin 25^o^.sin 35^o^.sin 60^o^.sin 85^o=sin 20^o^.sin 40^o^.sin 75^o^.sin 80^o.

(5 points)

B. 3611. The infinite series 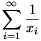$\sum_{i=1}^{\infty}\frac{1}{x_i}$ is formed out of the elements of the sequence defined by the recursion x_n+1=x_n²-x_n+1. What is the sum of the series if a) x₁=1/2; b) x₁=2? (5 points)

New advanced problems

Maximum score for each advanced problem (sign "A") is 5 points.

A. 308. A, B, C, D, E are points in the plane, such that AB=BC=CD=DA=1, and each of AE, BE, CE and DE is at most 1. What is the maximum possible value of AE+BE+CE+DE+AC+BD?

A. 309. In a simple graph on n points, the orders of the points are 0<d₁ $\le$ ... $\le$ d_n. Prove that it is possible to select at least $\displaystyle \sum\frac{2}{d_i+1}$ points, such that the subgraph formed by these points contains no loop.

A. 310. Let 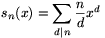$s_n(x)=\sum_{d\mid n}\frac{n}{d}x^d$ , for every positive integer n, and define the polynomials p₀,p₁,... by the following recursion: p₀(x)=1, 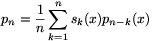$p_n=\frac{1}{n} \sum_{k=1}^ns_k(x)p_{n-k}(x)$ . Prove that the coefficients of the polynomial p_n are all integers.

Send your solutions to the following address:

or by e-mail to:

solutions@komal.hu

Already signed up?
New to KöMaL?