A 2003. februári B-jelű matematika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

B.3612. Egy tízes számrendszerben felírt számból kiindulva készítsük el a szám jegyeinek permutációival nyerhető különböző számok összegét. Pl. a 110-ből kiindulva a 110+101+11=222 összeg adódik. Melyik a legkisebb szám, amelyből kiindulva a kapott összeg 4 933 284?

(4 pont)

Javasolta: Bakonyi Gábor, Budapest

Megoldás: A keresett szám legalább ötjegyű. Ugyanis legfeljebb négyjegyű számból kiindulva legfeljebb 24 számot készíthetünk el, és ezért az összeg kisebb lesz, mint 240000. Ha van ilyen ötjegyű szám, akkor a legkisebb ilyen szám is ötjegyű lesz. Ha egy abcde ötjegyű szám minden jegye különböző, akkor belőle 120 számot tudunk felírni, és bármelyik helyiértéket is tekintjük, pontosan 24 olyan szám lesz ezek között, amelyik az adott helyiértéken az a,b,c,d,e számjegyek közül egy előre rögzítettet tartalmaz. A felírt 120 szám összege ennek megfelelően

11111^.24^.(a+b+c+d+e).

Mivel a 4933284:11111=444 szám 24-gyel nem osztható, a keresett ötjegyű számnak nem lehet mind az öt jegye különböző.

Ha a keresett számnak legfeljebb 3 különböző számjegye lenne, akkor könnyen ellenőrizhető, hogy minden egyes számjegy minden egyes helyiértéken legfeljebb 12-szer fordulhatna elő, ami miatt a jegyek permutációival kapható számok összege nem lenne nagyobb, mint

11111^.12^.(9+8+7)<4933284.

Ha tehát van ilyen ötjegyű szám, akkor annak négy különböző számjegye van, a,b,c és d, melyek közül valamelyik, mondjuk d, kétszer szerepel. Ekkor 60 különböző számot lehet elkészíteni, melyek között, bármely helyiértéket rögzítjük is le, pontosan 12 olyan lesz, amely ott az a számjegyet tartalmazza (és ugyanez mondható el a b, illetve a c számjegyekkel kapcsolatban is), és 24 olyan lesz, amely ott a d számjegyet tartalmazza, vagyis most

11111^.12^.(a+b+c+2d)=4933284,

ahonnan a+b+c+2d=37. Az utolsó négy helyen álló számjegy összege a 9+9+8+7=33 összeget nem haladhatja meg, amiértis az első számjegy legalább 4. Ha az első számjegy 4, akkor a második legalább 7, és ha az 7, akkor a harmadik számjegy legalább 8. Mindezek alapján a legkisebb szóba jövő ötjegyű szám a 47899, ez tehát a keresett szám.

B.3613.Egy $\displaystyle f\:R\to R$ függvényre bármely x, y számok esetén

|f(x)-f(y)|=|x-y|.

Mennyi lehet f(2) értéke, ha f(1)=3?

(3 pont)

Megoldás: Az első feltételt nyilván minden f(x)=x+a és minden f(x)=a-x alakú függvény kielégíti. Ha f(1)=3, akkor

|f(2)-3|=|f(2)-f(1)|=|2-1|=1 ,

ahonnan látszik, hogy f(2) értéke csakis 4 vagy 2 lehet. Mind a két lehetőség meg is valósítható, hiszen ha f(x)=x+2, akkor f(1)=3 és f(2)=4, ha pedig f(x)=4-x, akkor f(1)=3 és f(2)=2.

B.3614. A₁, A₂, ..., A_n a sík különböző pontjai. Színezzük pirosra az általuk meghatározott valamennyi szakasz felezőpontját. Mennyi a létrejövő piros pontok minimális száma?

(4 pont)

Javasolta: Némethy Katalin, Budapest

Megoldás: Ha n=1, akkor egyetlen felezőpont sem jön létre. Megmutatjuk, hogy ha n$\displaystyle ge$2, akkor a piros pontok minimális száma 2n-3. Először is, ha A_i a számegyenesen az i-1 számot kijelölő pont, akkor pontosan azok a pontok lesznek pirosak, melyek egy 0-nál nagyobb ám 2n-2-nél kisebb egész szám felét jelölik ki; ez éppen 2n-3 pont. Most már csak annyit kell megmutatnunk, hogy az A_i pontok tetszőleges elhelyezkedése esetén lesz ennyi piros pont.

Ezt n szerinti indukcióval igazolhatjuk könnyedén. Ha n=2, akkor mindig pontosan 1 piros pont jön létre. Ha pedig n pont mindig legalább 2n-3 piros pontot határoz meg, akkor az A₁,...,A_n+1 pontokból kiindulva, először is rajzoljuk meg a $\displaystyle {\cal P}=\{A_1,\ldots,A_{n+1}\}$ halmaz $\displaystyle \cal C$ konvex burkát. Legyen ennek egy csúcsa B, e pedig legyen olyan egyenes, amely $\displaystyle \cal C$-t B-ben érinti. Legyen még B₁ és B₂ a $\displaystyle {\cal P}\setminus\{B\}$ halmaz két olyan pontja, mely az e egyeneshez lehető legközelebb helyezkedik el.

Mármost a $\displaystyle {\cal P}\setminus\{B\}$ halmaz indukciós feltevésünk szerint legalább 2n-3 piros pontot határoz meg; legyen ezek halmaza $\displaystyle \cal F$. A B₁B és a B₂B szakaszok felezőpontja nem esik egybe, és nem lehet eleme $\displaystyle \cal F$-nek sem, hiszen mindkét pont közelebb esik az e egyeneshez, mint a B₁B₂ szakasz F felezőpontja, míg $\displaystyle \cal F$ pontjai legalább olyan távol vannak az e-től, mint F. Ez tehát két újabb piros pont, vagyis a $\displaystyle \cal P$ halmaz legalább (2n-3)+2=2(n+1)-3 piros pontot határoz meg, ahogyan azt az indukciós lépéshez igazolnunk kellett.

B.3615. Egy egységnyi élű paralelepipedon alaplapja A₁A₂A₃A₄, fedőlapja B₁B₂B₃B₄ úgy, hogy az A_i és B_i csúcsokat él köti össze. Milyen határok között változik az A₁B₂²+A₂B₃²+A₃B₄²+A₄B₁² négyzetösszeg?

(3 pont)

Megoldás: Jelölje az A₁A₂B₂, A₂A₃B₃, A₃A₄B₄ és A₄A₁B₁ szögeket rendre $\displaystyle alpha$,$\displaystyle beta$,$\displaystyle gamma$,$\displaystyle delta$; ekkor $\displaystyle gamma$=$\displaystyle pi$-$\displaystyle alpha$ és $\displaystyle delta$=$\displaystyle pi$-$\displaystyle beta$. A koszinusz tétel alapján

A₁B₂²=A₁A₂²+A₂B₂²-2A₁A₂^.A₂B₂cos$\displaystyle alpha$=2-2cos$\displaystyle alpha$ .

Ugyanígy az összeg többi tagjára 2-2cos$\displaystyle beta$, 2-2cos$\displaystyle gamma$ és 2-2cos$\displaystyle delta$ adódik. Mivel cos$\displaystyle gamma$=-cos$\displaystyle alpha$ és cos$\displaystyle delta$=-cos$\displaystyle beta$, a szóban forgó összeg értéke minden esetben 8-cal egyenlő.

B.3616. A derékszögű koordinátarendszer (1;1) pontján átmenő e, valamint a (-1;1) pontján átmenő f egyenesekről tudjuk, hogy meredekségük különbsége 2. Határozzuk meg az e és f egyenesek metszéspontjának mértani helyét.

(3 pont)

Megoldás: Jelölje a két egyenes meredekségét a+1 és a-1. Ha az e egyenes egyenlete y=(a+1)x+b, az f egyenesé pedig y=(a-1)x+c, akkor a feltételekből a+1+b=1, illetve 1-a+c=1 adódik, vagyis b=-a és c=a. Az (a+1)x-a=(a-1)x+a egyenletet megoldva az e és f egyenesek (x,y) metszéspontjára x=a adódik, ahonnan y=a², vagyis a metszéspont az y=x² egyenletű parabolán helyezkedik el, és a parabola minden pontja alkalmas két ilyen egyenes metszéspontja.

Ha az e egyenes egyenlete y=(a-1)x+b, az f egyenesé pedig y=(a+1)x+c, akkor a helyettesítéssel most b=2-a és c=a+2 adódik, ahonnan a metszéspont koordinátái x=-a, y=2-a² lesznek. Ezek a metszéspontok tehát az y=2-x² parabola pontjai lesznek.

Összefoglalva, az egyenesek metszéspontjának mértani helye két parabola, melyek éppen a feladatban szereplő két pontban metszik egymást. Az egyik parabola a jól ismert y=x² függvény grafikonja, a másik parabola ennek az y=1 egyenesre vett tükörképe.

B.3617. A t paraméter milyen értékeire van az

x+y+z+v =0, (xy+yz+zv)+t(xz+xv+yv) =0

egyenletrendszernek pontosan egy megoldása?

(5 pont)

Megoldás: Az első egyenletből v-t kifejezve, majd azt a második egyenletbe behelyettesítve látható, hogy az egyenletrendszernek pontosan azon t értékekre van egyetlen megoldása, amelyek mellett a

z²+(x+ty)z+t(x+y)²-xy=0

egyenletnek is pontosan egy megoldása van. Ez rögzített t,x,y érékek mellett z-ben másodfokú egyenlet. Ezért azon t értékeket kell meghatároznunk, amelyekre bármely x,y érték mellett az egyenlet

D_xy=(x+ty)²-4t(x+y)²+4xy

diszkriminánsa nem pozitív, és a D_xy=0 egyenletnek pedig csak egyetlen megoldása van. Mivel D_xy=(1-4t)x²+(4-6t)xy+(t²-4t)y², t<1/4 esetén D_xy pozitív értékeket is felvesz. Ha t=1/4, akkor D_xy=(5/2)xy-(15/16)y², mely esetben a D_xy=0 egyenletnek végtelen sok megoldása van.

Végül x>1/4 esetén rögzített t,y értékek mellett D_xy x-ben másodfokú polinom, melynek főegyütthatója negatív. Ezért pontosan azokat a t értékeket kell meghatároznunk, amelyek mellett bármely y-ra a polinom

D_y=((4-6t)y)²-4(1-4t)(t²-4t)y²

diszkriminánsa nem pozitív, a D_y=0 egyenletnek pedig csak egyetlen megoldása van. Ez pedig nyilván pontosan akkor teljesül, ha

f(t)=(4-6t)²-4(1-4t)(t²-4t)=16(t+1)(t²-3t+1)<0.

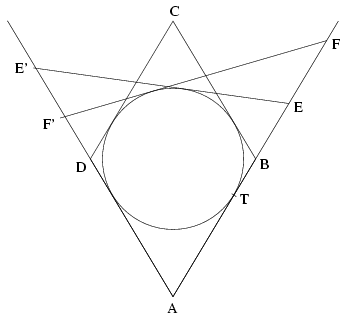
Mivel az f(t)=0 egyenlet gyökei növekvő sorrendben -1, $\displaystyle (3-\sqrt{5})/2$ és $\displaystyle (3+\sqrt{5})/2$, továbbá f főegyütthatója pozitív, az f(t)<0 feltétel pontosan akkor teljesül, ha vagy t<-1, vagy pedig \(\displaystyle (3-\sqrt{5})/2t>1/4 feltétellel is egybevetve kapjuk, hogy az egyenletrendszernek akkor és csak akkor van pontosan egy megoldása, ha

\(\displaystyle {3-\sqrt{5}\over2}

B.3618. Az ABCD rombusz AB oldalának B-n túli meghosszabbításán lévő E és F pontokból a rombusz beírt köréhez húzott érintők az AD egyenest az E' és F' pontokban metszik. Határozzuk meg a DE':DF' arányt, ha tudjuk, hogy BE:BF=$\displaystyle \lambda$:$\displaystyle \mu$.

(4 pont)

Megoldás:

Jelölje a beírt kör sugarát r, T pedig azt a pontot, amelyben az AE szakasz a kört érinti. Az E'AE, AEE' és EE'A szögeket jelölje rendre 2$\displaystyle alpha$,2$\displaystyle beta$,2$\displaystyle gamma$, ekkor $\displaystyle beta$+$\displaystyle gamma$=90^o-$\displaystyle alpha$. Ezen jelölésekkel BE=TE-TB=r(1/tan$\displaystyle beta$-tan$\displaystyle alpha$). Ugyanígy DE'=r(1/tan$\displaystyle gamma$-tan$\displaystyle alpha$). Lévén

$\displaystyle \tan\alpha={1\over\tan(\beta+\gamma)}={1-\tan\beta\tan\gamma\over\tan\beta+\tan\gamma}\ ,$

a DE' szakaszt is hasonlóképpen kifejezve kapjuk, hogy

$\displaystyle BE\cdot DE'=r^2\Bigl({1\over\tan\beta}-\tan\alpha\Bigr)\Bigl({1\over\tan\gamma}-\tan\alpha\Bigr)=$

$\displaystyle =r^2\Bigl({1-(\tan\beta+\tan\gamma)\tan\alpha\over\tan\beta\tan\gamma}+\tan^2\alpha\Bigr)=r^2(1+\tan^2\alpha)\ ,$

mely kifejezés értéke független az E pont választásától. Emiatt BF^.DF'=BE^.DE', vagyis DE':DF'=BF:BE=$\displaystyle mu$:$\displaystyle lambda$.

B.3619. Tekintsünk három olyan síkot, amelyek egy egységnyi térfogatú tetraéder egy-egy lapjával párhuzamosak és felezik a tetraéder térfogatát. Mekkora annak a tetraédernek a térfogata, amelyet ez a három sík és a tetraéder negyedik lapja határol?

(4 pont)

Megoldás: Jelölje az eredeti tetraédert T, annak magasságát pedig m. Az első sík T-ből egy hozzá hasonló T₁ tetraédert vág le, ahol a hasonlóság aránya $\displaystyle 1/{\root3\of{2}}$. Ezért a T₁ tetraéder magassága $\displaystyle m_1=m(1/{\root3\of{2}})$, a szóben forgó síknak T vele párhuzamos lapjától vett távolsága pedig $\displaystyle d=m(1-1/{\root3\of{2}})$. A második sík T₁-ből egy hozzá és T-hez is hasonló T₂ tetraédert vág le. Mivel ez a sík is d távolságra van a T vele párhuzamos lapjától, ami egyben T₁-et is határolja, a T₂ tetraéder magassága m₂=m₁-d=m-2d. Ugyanilyen alapon a harmadik sík T₂-ből egy m₃=m-3d magasságú T₃ tetraédert vág le, mely szintén hasonló T-hez, ahol a hasonlóság aránya $\displaystyle lambda$=(m-3d)/m.

A feladatban éppen ennek a tetraédernek a térfogatát kell meghatároznunk. Mivel T térfogata egységnyi, T₃ térfogata éppen

$\displaystyle \lambda^3=\Bigl({3\over{\root3\of{2}}}-2\Bigr)^3={(3-2{\root3\of{2}})^3\over2}={11\over2}-27{\root3\of2}+18{\root3\of{4}}.$

B.3620. Tegyük fel, hogy az

$\displaystyle a_{n+1}=\frac{1}{1-a_n}-\frac{1}{1+a_n} $

rekurzióval képzett sorozat periodikus. Mi lehet a sorozat első eleme?

(5 pont)

Javasolta: Zsíros Péter, Szombathely

Megoldás: Mivel a tangens függvény értékkészlete az egész számegyenes, van olyan $\displaystyle alpha$ szög, amelyre a₁=tan$\displaystyle alpha$. Ekkor a₂=2a₁/(1-a₁²)=tan2$\displaystyle alpha$, és általában a_k+1=tan2^k$\displaystyle alpha$. Ezek szerint, ha valamilyen pozitív egész k-ra a_k+1=a₁, akkor alkalmas t egész számmal 2^k$\displaystyle alpha$=$\displaystyle alpha$+t$\displaystyle pi$. A sorozat tehát pontosan akkor periodikus, ha

$\displaystyle \arctan a_1={t\over2^k-1}\pi$

teljesül alkalmas t egész számra és k pozitív egészre. Ebből világosan látszik, hogy végtelen sok megfelelő kezdőérték van; ilyen például az $\displaystyle a_1=\sqrt{3}$, amit a k=2, t=1 esetből kaphatunk meg.

B.3621. Legyen f(x)=ax+1, ahol a$\displaystyle \ne$0 adott valós szám. Keressük meg azokat a g(x) polinomokat, amelyekre f(g(x))=g(f(x)).

(5 pont)

Megoldás: Egy g(x)=c konstans polinom pontosan akkor megfelelő, ha ac+1=c, vagyis ha a$\displaystyle ne$1 és g(x)=c=1/(1-a). Egy g(x)=bx+c elsőfokú polinom pedig pontosan akkor lesz jó, ha minden x-re a(bx+c)+1=b(ax+1)+c, vagyis ha ac+1=b+c. Ha a=1, akkor tehát a g(x)=x+c alakú polinomokról van szó, ahol c tetszőleges valós szám lehet, egyébként pedig a g(x)=bx+(b-1)/(a-1) alakú polinomokról, ahol b$\displaystyle ne$0.

Ha g(x) n-edfokú polinom (n$\displaystyle ge$2), akkor főegyütthatóját c_n-nel jelölve, f(g(x)) egy olyan n-edfokú polinom, amelynek főegyütthatója ac_n, g(f(x)) pedig egy olyan n-edfokú polinom, melynek főegyütthatója aⁿc_n. Ezért ekkor a^n-1=1, vagyis a=$\displaystyle pm$1.

Ha a=1, akkor feltételünk a g(x)+1=g(x+1), vagyis g(x+1)-g(x)=1 alakot ölti. Ez azonban nem lehet, minthogy g^-(x)=g(x+1)-g(x) egy n-1-edfokú polinom. Valóban, ez még akkor is igaz, ha g(x) lineáris, ha pedig n$\displaystyle ge$2 és az állítást 1$\displaystyle le$m$\displaystyle le$n-1 esetén m-edfokú polinomokra már igazoltuk, akkor a g(x)=c_nxⁿ+h(x) jelöléssel élve, ahol h(x) legfeljebb n-1-edokú polinom, kapjuk hogy

$\displaystyle g^-(x)=c_n(x+1)^n+h(x+1)-c_nx^n-h(x)=nc_nx^{n-1}+\sum_{i=2}^n{n\choose i}c_nx^{n-i}+h^-(x),$

ami indukciós feltevésünk alapján egy nc_n főegyütthatós n-1-ed fokú polinom.

Végül ha a=-1, akkor a feltételünk g(-x+1)+g(x)=1, ami h(x)=g(x+1/2), vagyis g(x)=h(x-1/2) helyettesítéssel (ahol h(x) tehát egy alkalmas n-edfokú polinom) a h(y)+h(-y)=1 alakot ölti. Ez pedig pontosan akkor teljesül, ha h(x) konstans tagja 1/2, ezen kívül azonban kizárólag páratlan fokú tagok szerepelnek benne.

Összefoglalva, megállapíthatjuk, hogy ha a$\displaystyle ne$ $pm$ 1, akkor a keresett polinomok éppen a g(x)=bx+(b-1)/(a-1) alakú polinomok (ez b=0 esetén pont a megfelelő konstans polinomot szolgáltatja); ha a=1, akkor a g(x)=x+c alakú polinomokról van szó; a=-1 esetén pedig azokról a polinomokról, amelyek alkalmas c₀,...,c_m valós számokkal (ahol m nemnegatív egész)

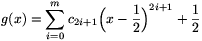
$g(x)=\sum_{i=0}^mc_{2i+1}\Bigl(x-{1\over2}\Bigr)^{2i+1}+{1\over2}$

alakba írhatók (ez a konstans és elsőfokú eseteket is magában foglalja), mint például a g(x)=x³-(3/2)x²+3/4x+3/8 polinom.

Már regisztráltál?
Új vendég vagy?