Exercises and problems in Physics
February 2003

Please read The Conditions of the Problem Solving Competition.

Experimental problem

M. 240. Investigate the monochromaticity of different LEDs (light-emitting diodes) with optical grating. Determine in which interval is the wavelength of the emitted light.

(6 points)

Theoretical problems It is allowed to send solutions for any number of problems, but final scores of students of grades 9-12 are computed from the 5 best score in each month. Final scores of students of grades 1-8 are computed from the 3 best scores in each month.

P. 3591. Through the 3.5 m wide exit of an underground station 70 people are leaving each minute on average. The ``population density'' is 0.4 heads/m². How much is the average velocity of the people?

(3 points)

P. 3592. There is a circuit without any branches consisting of a galvanic cell, a battery and an ohmic resistance. The voltages that can be measured at the battery and at the resistance are both 9 V. What voltage can be measured at the galvanic cell (also 9 V) of non-zero internal resistance, and what can be said of the actual magnitude of the resistance?

(4 points)

P. 3593. A horizontal disc magnet of radius R rotates with an angular velocity of \(\displaystyle \omega\)₀ around a fixed vertical axis going through its center. A similar horizontal disc, initially motionless, falls from a small distance on it and instantly sticks to it. (The centers of the two discs are closer to each other than R.) What is the common angular velocity the two discs rotate with?

(4 points)

P. 3594. A line pendulum is diverted perpendicularly, and released without pushing. Which section in the figure does the pendulum cover in a shorter time, AP or PB?

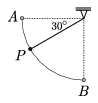
(5 points)

P. 3595. We prepare a hemisphere shaped depression inside a prism. The prism of mass M can freely move on the horizontal table. We release a point-like body of mass m at point P of the resting prism. What force does the prism exert on the small body in its state of angle \(\displaystyle \varphi\)? (Friction is negligible everywhere.)

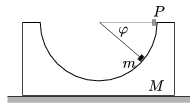
(5 points)

P. 3596. There is oxygen gas in a 3 liter tank of a pressure of 2.2^.10⁶ Pa and a temperature of 80 ^oC, and in a 5 liter one of a pressure of 1.3^.10⁵ Pa and of a temperature of 5 ^oC. The two tanks are connected with a short pipe. What is the common pressure inside the tanks after they reach the room temperature, 23 ^oC? How much gas has flown through the pipe in the meantime?

(4 points)

P. 3597. A certain amount of noble gas picks up a Q amount of heat while its volume increases from V₁ to V₂, and its pressure is proportionate to its volume. To what volume would the gas expand from the initial V₁ volume if it absorbed heat Q while preserving its initial pressure? (The data: V₁=5 dm³, V₂=8 dm³.)

(4 points)

P. 3598. The plates of area A of a plane-parallel capacitor can slide along a horizontal insulator thread without friction. The mass of the left-side plate is m and its electric charge is Q, the mass of the right-side plate is 2m and its electric charge is -2Q. Initially the pates are fixed and their distance is 3d.

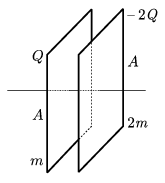
a) What is the energy of the electric field between the plates?

b) At a given moment they are unfixed. What is their velocity when their distance is reduced to d?

(5 points)

P. 3599. In Debrecen in 1984 it was determined that the activity concentration of the beta decay of the ⁸⁵Kr isotope, generated as a possible product of nuclear fission, is 0.8 Bq/m³. Estimate how many krypton nuclei decay in one hour in the atmosphere.

(5 points)

P. 3600. Two grounded metal plates of large extents are including an \(\displaystyle \alpha\) angle with each other. In the bisector plane, in an r distance of the intersection line there is a thin stick of length L (L\(\displaystyle \gg\)r) which is charged uniformly with an overall electric charge of Q. What force is exerted on the stick due to the electrostatic induction, if a) \(\displaystyle \alpha\)=180^o, b) \(\displaystyle \alpha\)=18^o.

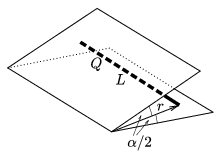
(5 points)

Send your solutions to the following address:

KöMaL Szerkesztőség (KöMaL feladatok),
Budapest 112, Pf. 32. 1518, Hungary

solutions@komal.hu.

Deadline: 11 March 2003