Exercises and problems in Informatics March 2003

Please read The Conditions of the Problem Solving Competition.

I. 46. Suppose we are given the set H={1,2,...,N} (1\(\displaystyle \le\)N\(\displaystyle \le\)1000) and two of its arbitrary subsets A,B \(\displaystyle \subset\)H both having exactly K (1\(\displaystyle \le\)K\(\displaystyle \le\)N-1) elements. We say that the set A is less than the set B, if the maximal element of \(\displaystyle A\setminus B\) is less than that of \(\displaystyle B\setminus A\). Write a program (i46.pas, ...) which reads the values of N, K and L, then gives the L^th largest subset of H with K elements.

Example: if N=5 and K=2, then the L=1^st subset is {5,4}, L=2^nd subset is {5,3}, L=5^th subset is {4,3}, L=10^th subset is {2,1}. (10 points)

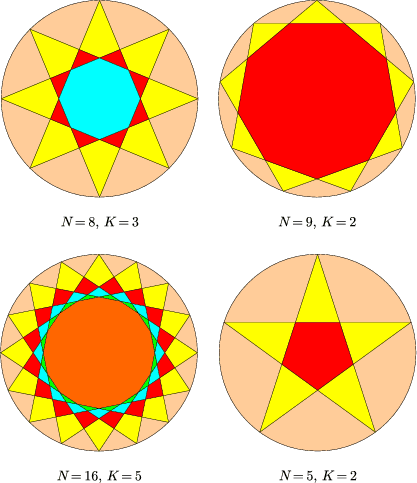
I. 47. Prepare a program (i47.pas, ...) which first displays a circle together with a regular N-gon (3\(\displaystyle \le\)N\(\displaystyle \le\)50) on its circumference (with one vertex at the top of the circle), then connects this topmost point with the K^th (1\(\displaystyle \le\)K\(\displaystyle \le\)N/2) vertex counterclockwise, then that one with the 2K^th vertex and so on, until we get back to the original point. The program should finally colour the figure in such a way that closed regions of similar type have the same, while those of different type have different colours, see the Figures.
(10 points)

I. 48. There is a class of N (1\(\displaystyle \le\)N\(\displaystyle \le\)20) students. We are interested in the number of ways of dividing them into K non-empty groups.

If N is entered, your sheet (i48.xls) should compute the number of possible ways a class of I (I=1,2,...,N) students can be divided into K non-empty groups, then display the result in the I^th row and K^th column of the framed area in the Figure. If the corresponding field makes no sense, then no value should be displayed in that position.
(10 points)

Send your solutions to the following e-mail address:

infotech@komal.elte.hu.

Deadline: 13 April 2003