 |
A 2003. áprilisi B-jelű matematika feladatok megoldása |
A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.
B.3632.
Oldjuk meg az x2003- [x]2003= (x-[x])2003 egyenletet a valós számok körében.(3 pont)
Megoldás: Ha x egész szám, akkor mindkét oldalon 0 áll. Ha nem, akkor legyen x=n+\(\displaystyle \alpha\), ahol n=[x] egész és 0<\(\displaystyle \alpha\)<1. Ekkor egyenletünk
(n+\(\displaystyle \alpha\))2003-n2003=\(\displaystyle \alpha\)2003,
amit (n+\(\displaystyle \alpha\))-n=\(\displaystyle \alpha\)-val elosztva az
(n+\(\displaystyle \alpha\))2002+n(n+\(\displaystyle \alpha\))2001+n2(n+\(\displaystyle \alpha\))2000+...+n2002=\(\displaystyle \alpha\)2002
egyenlet adódik. Ez nyilván teljesül, ha n=0. Jegyezzük meg, hogy a jobboldalon 0 és 1 közé eső szám áll. Ha n\(\displaystyle \ge\)1, akkor a baloldalon minden összeadandó értéke legalább 1, ezért az egyenlőség nem állhat fenn. Ugyanez a helyzet akkor is, ha n\(\displaystyle \le\)-2, hiszen ekkor minden összeadandó páros sok -1-nél kisebb szám szorzata. Végül ha n=-1, akkor az eredeti egyenlet átrendezésével az
1=\(\displaystyle \alpha\)2003+(1-\(\displaystyle \alpha\))2003
egyenlethez jutunk, azonban 0<\(\displaystyle \alpha\)<1 és 0< 1-\(\displaystyle \alpha\)<1 miatt
\(\displaystyle \alpha\)2003+(1-\(\displaystyle \alpha\))2003<\(\displaystyle \alpha\)+(1-\(\displaystyle \alpha\))=1.
Összefoglalva, az egyenlet megoldásai az egész számok, valamint a 0 és 1 közé eső valós számok.
B.3633.
Egy konvex négyszöget átlói négy olyan háromszögre darabolnak, melyek mindegyikének egész szám a területe.Lehet-e ezek közül három szám 2001, 2002 és 2003?
(3 pont)
Hajdú-Bihar megyei középiskolák matematika versenye 2002/2003
Megoldás: Jelölje a négy háromszög területét valamilyen körüljárási irány szerinti sorrendben a,b,c és d. Tegyük fel, hogy az első három szám valamilyen sorrendben megegyezik a 2001, 2002 és 2003 számokkal. Az a és b területű háromszögek egyik magassága közös, ezért a/b megegyezik a megfelelő alapok hányadosával. Ugyanez mondható el a d és c területű háromszögekről is. Mivel az a és d területű háromszögek alapja megegyezik, és ugyanígy a b és c területű háromszögeké is, kapjuk, hogy a/b=d/c, azaz d=ac/b. Mivel a 2001, 2002 és 2003 számok közül egyik sem osztója a masik kettő szorzatának, d nem lehet egész szám. Ezért a feladatban feltett kérdésre nemleges a válasz.
B.3634.
Legyen k(n) az n legnagyobb páratlan osztója és\(\displaystyle f(n)=\sum_{i=1}^nk(i). \)
Bizonyítsuk be, hogy f(2n)-f(n)=n2.
(4 pont)
Megoldás: Nyilván k(2m)=k(m), tehát
f(2n)=k(1)+k(2)+k(3)+...+k(2n-1)+k(2n)=
=[k(1)+k(3)+...+k(2n-1)]+[k(2)+k(4)+...+k(2n)]=
[1+3+...+(2n-1)]+[k(1)+k(2)+...+k(n)]=n2+f(n),
amiből az állítás már következik.
B.3635.
Egy konvex poliédernek c csúcsa van. Mutassuk meg, hogy a poliéder lapjain levő belső szögek összege együttesen (c-2).360o.(4 pont)
Megoldás: Ha a poliédernek \(\displaystyle \ell\) lapja és e éle van, akkor Euler tétele szerint e=\(\displaystyle \ell\)+c-2. Az egyes lapoknak legyen rendre \(\displaystyle e_1,e_2,\ldots,e_\ell\) éle. Mivel a poliéder minden egyes éle pontosan két lapnak lesz határoló éle,
\(\displaystyle e_1+e_2+\ldots+e_\ell=2e.\)
Ha egy lapnak ei éle van, akkor belső szögeinek összege (ei-2)\(\displaystyle \pi\), ezért a lapokon lévő belső szögek összege együttesen
\(\displaystyle \sum_{i=1}^\ell(e_i-2)\pi= \Bigl(\sum_{i=1}^\ell e_i-2\ell\Bigr)\pi= (2e-2\ell)\pi=2(c-2)\pi,\)
ahogy azt bizonyítani kívántuk.
B.3636.
Mi a feltétele annak, hogy létezzék olyan hat szakaszból álló zárt töröttvonal, amelynek oldalai adott sorrendben a, b, c, d, e, f, és a szemközti oldalak merőlegesek egymásra?(5 pont)
Megoldás: Tegyük fel, hogy ABCDEFA ilyen zárt töröttvonal, ahol AB=a, BC=b, CD=c, DE=d, EF=e, FA=f. Tükrözzük az A pontot a BF szakasz felezőpontjára, az így kapott A' pontra A'B=FA=f és FA'=AB=a. Továbbá ezek az egymással egyenlő hosszúságú szakaszok egyben párhuzamosak is, amiért is az A'B szakasz merőleges a CD szakaszra, az FA' szakasz pedig a DE szakaszra.
Ugyanígy a C pontot a BD oldal felezőpontjára, az E pontot pedig a DF oldal felezőpontjára tükrözve, olyan A'BC'DE'FA' zárt töröttvonalhoz jutunk, melynek oldalai A'B=f, BC'=c, C'D=b, DE'=e, E'F=d, FA'=a, és az A'B, C'D, E'F szakaszok rendre merőlegesek a BC', DE', FA' szakaszokra. Az A'C'E' pontok tehát olyan, esetleg elfajuló háromszöget határoznak meg, melynek oldalai \(\displaystyle \sqrt{f^2+c^2}\), \(\displaystyle \sqrt{b^2+e^2}\) és \(\displaystyle \sqrt{d^2+a^2}\). Szükséges feltétel tehát, hogy ezen három szakasz közül egyik se legyen nagyobb a másik kettő összegénél.
Ez a feltétel egyben elégséges is. Ugyanis ha a \(\displaystyle \sqrt{f^2+c^2}\), \(\displaystyle \sqrt{b^2+e^2}\) és \(\displaystyle \sqrt{d^2+a^2}\) szakaszokból megszerkesztjük az esetleg elfajuló A'C'E' háromszöget, majd ennek oldalaira a megfelelő A'BC', C'DE', E'FA' derékszögű háromszögeket, ahol A'B=f, BC'=c, C'D=b, DE'=e, E'F=d és FA'=a (erre az általános esetben 8 különféle lehetőségünk van), akkor az A',C',E' pontokat rendre az FB,BD,DF szakaszok felezőpontjára tükrözve a feltételeknek megfelelő ABCDEFA zárt töröttvonalat kapunk.
B.3637.
Fel lehet-e venni a kocka minden élén egy-egy pontot úgy, hogy a 12 pont konvex burkának térfogata éppen a kocka térfogatának fele legyen?(4 pont)
Megoldás: Tekintsük az egységnyi élű kockának négy olyan csúcsát, melyek közül semelyik kettő nem szomszédos, és az ezekből induló éleken vegyünk fel a kiindulási csúcstól x távolságra egy-egy pontot (0<x<1). Ilyen módon a kocka minden egyes élén kijelöltünk egy belső pontot. Ezen pontok konvex burkát megkaphatjuk úgy, hogy a kockából minden egyes csúcsnál levágunk egy alkalmas tetraédert. Ezek a tetraéderek nem nyúlnak egymásba, közülük négynek a térfogata x3/6, a másik négyé pedig (1-x)3/6. Ha x megválasztható úgy, hogy e tetraéderek térfogatának összege 1/2 legyen, akkor a 12 pont konvex burkának térfogata éppen a kocka térfogatának fele lesz. Feltételünk tehát
4x3+4(1-x)3=3,
vagyis 12x2-12x+1=0. Mivel az egyenlet gyökei, \(\displaystyle (1/2)\pm\sqrt{1/6}\) 1-nél kisebb pozitív számok, a feladat megvalósítható.
B.3638.
A sík egy \(\displaystyle \ell\) egyeneséről azt mondjuk, hogy érinti a H ponthalmazt, ha H-nak pontosan egy pontja illeszkedik \(\displaystyle \ell\)-re. Adjunk meg a síkon olyan ponthalmazt, melynek minden pontjában pontosan egy érintője van és a sík minden egyenesén van legalább egy pontja.(5 pont)
Megoldás: Vegyünk fel egy e egyenest, valamint erre merőlegesen az f és g egyeneseket, melyek az e egyenest rendre az F és G pontokban metszik. A \(\displaystyle H=e\cup f\cup g\setminus\{F,G\}\) ponthalmaznak a sík minden h egyenesén van pontja, ugyanis ha h nem párhuzamos e-vel, akkor metszi e-t és ha ez a metszéspont véletlenül egybeesik az F (vagy a G) ponttal, akkor h a H halmazt metszi a g (vagy az f) egyenesen, ha pedig h párhuzamos e-vel, akkor vagy egybeesik vele, vagy pedig metszi H-t mind az f, mind a g egyenesen.
Másrészt ha P H-nak egy pontja az e egyenesen, akkor P-n keresztül H-hoz pontosan egy érintő húzható, nevezetesen az, amelyik e-re merőleges. Ha P H-nak az f egyenesen lévő pontja, akkor az egyetlen P-n áthaladó érintő a PG egyenes lesz. Ha pedig P H-nak az g egyenesen lévő pontja, akkor az egyetlen P-n áthaladó érintő a PF egyenes. A H ponthalmaz tehát megfelelő lesz.
B.3639.
Vegyünk fel az AB szakasz A-n túli meghosszabbításán egy C pontot. A C pontban az AB egyenesre állított merőleges legyen e. Legyen D az e tetszőleges pontja és állítsunk AD-re merőlegest az A pontban. Ennek és DB-nek a metszéspontja legyen P.Mi a P pontok mértani helye?
(4 pont)
Javasolta: Blahota István, Nyíregyháza
Megoldás:
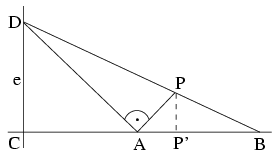
Ha D=C, akkor P=A, egyébként P-nek az AB egyenesre eső merőleges vetülete az AB szakasznak egy P' belső pontja lesz. Jelölje az AC, BC, DC szakaszok hosszát rendre a,b,d, a PAB és PBA szögeket pedig \(\displaystyle \alpha\) illetve \(\displaystyle \beta\). A feladat szövege szerint az ADC szög nagysága is \(\displaystyle \alpha\). Itt tan \(\displaystyle \alpha\)=a/d, míg tan \(\displaystyle \beta\)=d/b.
Ha P* a P'P félegyenesnek azon pontja, amelyre \(\displaystyle P'P^*=\sqrt{b/a}P'P\), akkor a P*AB és P*BA szögeket \(\displaystyle \alpha\)*-gal illetve \(\displaystyle \beta\)*-gal jelölve \(\displaystyle \tan\alpha^*=\sqrt{ab}/d\), míg \(\displaystyle \tan\beta^*=d/\sqrt{ab}\). Mivel a két hegyesszög tangensének szorzata 1, kapjuk, hogy \(\displaystyle \alpha\)*+\(\displaystyle \beta\)*=90o, vagyis P* az AB átmérőjű körvonal pontja. Ennek megfelelően, P azon az AB nagytengelyű ellipszisen helyezkedik el, amelyet az AB átmérőjű körből az AB-re merőleges, \(\displaystyle \sqrt{a/b}\) arányú affinitással származtathatunk.
A fenti gondolatmenet megfordításával könnyen látható, hogy az említett ellipszis minden egyes, B-től különböző pontja a mértani helyhez tartozik.
B.3640.
Legyena1=1 és \(\displaystyle a_{n+1}=a_n+\frac{1}{s_n}\),
ahol sn=a1+a2+...+an. Korlátos-e az an sorozat?
(5 pont)
Megoldás: Tegyük fel, hogy a sorozat korlátos, vagyis létezik olyan M pozitív szám, hogy an\(\displaystyle \le\)M a sorozat minden egyes elemére. Ekkor minden i-re si\(\displaystyle \le\)iM és így
\(\displaystyle a_{n+1}=a_n+{1\over s_n}=a_{n-1}+{1\over s_{n-1}}+{1\over s_n}= \ldots=a_1+\sum_{i=1}^n{1\over s_n\)\sum_{i=1}^n{1\over iM}>M,">
ha \(\displaystyle \sum_{i=1}^n{1\over i\)M^2">. Könnyen igazolhatjuk azonban, hogy n=2k esetén \(\displaystyle \sum_{i=1}^n{1\over i\)k/2">, vagyis ez az összeg akármilyen nagy lehet, akár M2-nél is nagyobb, mely esetben viszont an+1>M adódik. Ellenmondásra jutottunk tehát, vagyis a sorozat nem lehet korlátos.
B.3641.
Van-e olyan p1(x), p2(x),...,pn(x),... végtelen polinomsorozat, ahol pk(x) pontosan k-adfokú, pi(pj(x))= pj (pi(x)) minden (i,j) párra ésa) p2(x)=x2-2,
b) p2(x)=x2-3?
(5 pont)
Megoldás: A b) esetben a p3(x) polinomot ax3+bx2+cx+d alakban keresve a p2(p3(x))=p3(p2(x)) feltétel
(ax3+bx2+cx+d)2-3=a(x2-3)3+b(x2-3)2+c(x2-3)+d
alakba írható. A két hatodfokú polinomban először x6 együtthatóját összevetve a2=a adódik, vagyis a=1. A baloldalon az ötödfokú tag együtthatója 2ab=2b, míg a jobboldalon 0, ahonnan b=0. Ezt folytatva, x4 együtthatóját vizsgálva 2ac=-9a, c=-9/2 adódik, a harmadfokú tagokból 2ad=0 vagyis d=0, végül a másodfokúakból c2=27a+c=27+c, ami ellentmond a c=-9/2 feltételnek. Ebben az esetben tehát a válasz nemleges.
Az a) esetben ugyanígy okoskodva p3(x)=x3-3x számolható ki, most tehát még reménykedhetünk egy megfelelő polinomsorozat létezésében. A B. 3631. feladat alapján elegendő olyan polinomsorozatot keresni, melyre pi(p2(x))=p2(pi(x)) teljesül minden i pozitív egész esetén. A p1(x)=x, p2(x)=x2-2, p3(x)=x3-3x polinomok ezt a feltételt teljesítik, továbbá fennállnak a p3=xp2-p1 és p3p1-p22=x2-4 összefüggések is. Tegyük fel, hogy valamilyen k\(\displaystyle \ge\)3 egész számra már meghatároztuk az i-edfokú pi polinomokat (1\(\displaystyle \le\)i\(\displaystyle \le\)k) úgy, hogy minden 1\(\displaystyle \le\)i\(\displaystyle \le\)k esetén piop2=p2opi teljesül, továbbá minden 3\(\displaystyle \le\)i\(\displaystyle \le\)k esetén pi=xpi-1-pi-2 és pipi-2-pi-12=x2-4. Elég megmutatni, hogy ekkor a pk+1=xpk-pk-1 rekurzióval definiált k+1-edfokú polinomra is teljesül pk+1op2=p2opk+1 és pk+1pk-1-pk2=x2-4, ugyanis ez esetben a teljes indukció elve már garantálja a keresett végtelen polinomsorozat létezését.
Nézzük előbb a második feltételt. Feltevéseink alapján
pk+1pk-1-pk2=(xpk-pk-1)pk-1-(xpk-1-pk-2)2=
=xpkpk-1-pk-12-x2pk-12+2xpk-1pk-2-pk-22=
=x(xpk-1-pk-2)pk-1-pk-12-x2pk-12+2xpk-1pk-2-pk-22=
=xpk-1pk-2-pk-12-pk-22=pkpk-2-pk-12=x2-4,
ahogyan azt igazolni kívántuk. Ennek, és indukciós feltevéseinknek alapján
(pk+1op2)(x)=pk+1(x2-2)=(x2-2)pk(x2-2)-pk-1(x2-2)=
=(x2-2)(pk(x)2-2)-(pk-1(x)2-2)=x2pk(x)2-2pk(x)2-pk-1(x)2-2x2+6,
ugyanakkor
(p2opk+1)(x)=pk+1(x)2-2=(xpk(x)-pk-1(x))2-2=
=x2pk(x)2-2xpk(x)pk-1(x)+pk-1(x)2-2.
A kettő különbsége ezért
2xpk(x)pk-1(x)-2pk-1(x)2-2pk(x)2-2x2+8=
=2((pk+1(x)pk-1(x)-pk(x)2)-(x2-4))=0,
pk+1 definíciója és az imént bizonyított összefüggés alapján, ami az első feltételt is igazolja.

