Exercises and problems in Physics
May 2003

Please read The Conditions of the Problem Solving Competition.

Experimental problem

M. 243. Measure what the pressure is inside a well inflated tyre of a bicycle without using a pressure gauge. (Compare the result with the prescribed pressure value of a common car's tyre. Explain the difference.)

(6 points)

Theoretical problems It is allowed to send solutions for any number of problems, but final scores of students of grades 9-12 are computed from the 5 best score in each month. Final scores of students of grades 1-8 are computed from the 3 best scores in each month.

P. 3622. Is it possible to contrive a kaleidoscope looking into which one could see a seven-point star?

(3 points)

P. 3623. We want to pump up 3 kg of petrol (\(\displaystyle \varrho\)=860 kg/m³) per second from a big underground tank at a depth of 3 m. The cross-section of the outlet of the pump is 10 cm². What should the power of the pump be at the least?

(4 points)

P. 3624. The narrow tube with one of its ends sealed, shown in the figure, is in a vertical plane. In the 3L long horizontal part of the tube a mercury column of length L blocks some oxygen gas of length L. The outside air-pressure of p₀ equals with the pressure of a mercury column of height L. Increasing the temperature of the surroundings, the volume of the blocked gas doubles while the gas absorbs Q=7 J of heat from its surroundings.

a) How much work is done by the expanding gas?

b) How much heat would have been needed to triple rather than to double the volume of the gas?

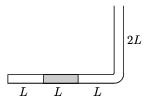
(5 points)

P. 3625. The work done by some gas during its adiabatic expansion in a cylinder closed by a piston is 9446 J. After the expansion we heat the gas until its temperature regains its original value. In the meantime the work done by the gas is 6140 J. How much is the \(\displaystyle \kappa\)=c_p/c_V ratio of the gas? Which gas can it be?

(4 points)

P. 3626. A thin-walled soap bubble filled with air is slowly heated. How much can the molar heat capacity of the gas be in this process? (The outside air-pressure is constant. Neglect the evaporation and the saturation vapor pressure.)

(5 points)

P. 3627. Alice and Bob are arguing on what kind of crystal lattice develops in a noble gas when cooled to such a low temperature that it solidifies. They agree that the densest possible array will develop. Alice says that the atoms will be arranged in parallel planes and form square lattices in the planes so that the atoms sit just above the ``gaps'' of the lattice below. Bob says that he would also apply this ``sitting in the gaps'' principle within the planes themselves and would rather arrange the atoms in a lattice of regular triangles. Who is right? What is the ``space filling'' of the spherical atoms in case A and B?

(5 points)

P. 3628. In a wood the trees are arranged randomly, so that there are 600 trees per hectare in average. The trunks of the trees can be considered cylinders of a diameter of 30 cm. At an outing the children play a game where one of them walks blindfold among the trees. The one blindfolded follows a straight line until he or she bumps into a tree then changes his or her course randomly. Estimate what distance the blindfolded child walks between the bumps on average, if he or she can also be considered a cylinder of a diameter of 30 cm.

(4 points)

P. 3629. How does the sum of gravitational energy and twice the kinetic energy change if the satellite is moved to a 100 km higher circular orbit?

(4 points)

P. 3630. Six point-like Q electric charges are placed in the vertices of a regular hexagon. What point charge is in the middle of the hexagon if the system is in the state of equilibrium? What is the electrostatic energy of the system? What kind of equilibrium is it?

(5 points)

P. 3631. After the Chernobyl-catastrophe the ¹³¹J activity of the thyroids of the local people was around 100 Bq. How long does it take for this activity to decrease under 100 Bq? The physical half-life of the 131 nucleon number iodine isotope is 8 days, and its biological half-life is 120 days.

(4 points)

Send your solutions to the following address:

KöMaL Szerkesztőség (KöMaL feladatok),
Budapest 112, Pf. 32. 1518, Hungary

solutions@komal.elte.hu.

Deadline: 11 June 2003