Fizikából kitűzött gyakorlatok és feladatok
2003. szeptember

Kérjük, olvassa el a versenykiírást.

Mérési feladat

M. 244. Mérjük meg néhány gyümölcsfajta százalékos víztartalmát!

(6 pont)

Közli: Gálfi László, Budapest

Az elméleti versenyben kitűzött gyakorlatok és feladatok Az elméleti fizika feladatokra kapható pontszám a feladatok nehézségétől függ. Az 1-8. osztályosok versenyében minden hónapban a 3 legnagyobb, a 9-12. osztályosok versenyeiben minden hónapban az 5 legnagyobb pontszám számít be a pontversenybe.

P. 3632. Két egyforma ladik közeledik a tó partjához. Mindkét csónakos kötél segítségével húzza magát a partra. Az egyik kötél a parton lévő bakhoz van erősítve, a másik kötél parti végét egy ember húzza. Melyik ladik ér célhoz hamarabb, ha feltételezzük, hogy mind a hárman ugyanakkora erőt fejtenek ki?

(4 pont)

Komárom-Esztergom-megyei Ifjú Fizikus verseny

P. 3633. 150 kg tömegű motoron 100 kg tömegű ember ül. A kerekek tengelyének távolsága 1,5 m. A motor és az ember együttes tömegközéppontja 1 m magasan van a talajszint felett, és 0,6 m távol van a hátsó tengelyen átmenő függőlegestől.

Mekkora erőt fejt ki a talaj a hátsó kerékre, amikor a=2 m/s² gyorsulással indul el a motor? Mekkora gyorsulással kell indulnia, hogy az első kerék felemelkedjék? Mekkora súrlódási együttható kell ehhez?

(4 pont)

Holló János fizikaverseny, Jászberény

P. 3634. 1 m hosszú, vékony, mindkét végén nyitott üvegcsövet félig vízbe nyomunk, majd a cső felső végét ujjunkkal befogjuk. Ezután lassan kiemeljük és megfordítjuk a csövet (az ujjunkkal befogott csővég alulra kerül, a csőben lévő víz fölülre).

Milyen hosszú a víz alá szorult levegőoszlop, ha a külső légnyomás 105 kPa?

(4 pont)

Károly Ireneusz fizikaverseny, Szombathely

P. 3635. Egy edényben 14 gramm nitrogén- és 9 gramm hidrogéngáz elegye van 17 ^oC hőmérsékleten és 100 kPa nyomáson.

Mekkora a gázelegy térfogata és belső energiája?

(3 pont)

Mikola Sándor fizikaverseny, Gyöngyös

P. 3636. Zárt, 4 liter térfogatú edényben normál nyomású és hőmérsékletű levegő, valamint 500 cm³ térfogatú és 1 gramm tömegű merev test van.

Mennyi levegőt kell még az edénybe pumpálni ahhoz, hogy a test felemelkedjék?

(3 pont)

Tarján Imre fizikaverseny, Szolnok

P. 3637. Egy termoszban levő 0 ^oC hőmérsékletű jégre 100 ^oC hőmérsékletű vízgőzt vezetünk.

Mekkora lehet a jég és a gőz tömegének aránya, hogy a termikus egyensúly kialakulása után a termoszban csak víz legyen?

(4 pont)

Párkányi László fizikaverseny, Pécs

P. 3638. Egy 40 ohmos tolóellenállás végeit 12 V-os akkumulátorra kötjük, majd egy 20 ohmos fogyasztót kapcsolunk a tolóellenállás egyik vége és a csúszka közé.

a) A csúszka mely állásánál kap a fogyasztó 6 V feszültséget?

b) Ebben az esetben a fogyasztó teljesítménye hány százaléka az akkumulátor által leadott teljesítménynek?

c) Mekkora a fogyasztó teljesítménye akkor, amikor a csúszka középen áll?

(4 pont)

Bay Zoltán fizikaverseny, Sarkad

P. 3639. Egy Q töltésű, m tömegű vékony gyűrű a középpontján átmenő, síkjára merőleges tengely körül forog. A gyűrű perdülete 7,5^.10^-4 kg^.m²/s. A gyűrű 0,1 T erősségű homogén mágneses mezőben van, melynek indukcióvonalai párhuzamosak a gyűrű síkjával. Mekkora forgatónyomaték hat a gyűrűre? A gyűrű fajlagos töltése: Q/m=10^-5 C/kg.

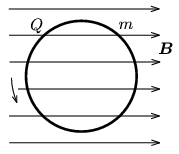
(4 pont)

Nagy László fizikaverseny, Kazincbarcika

P. 3640. Mekkora fókusztávolságú és milyen tükörben látjuk arcunkat a tisztánlátás távolságában (25 cm) másfélszeres nagyításban? Milyen messze tartjuk arcunktól a tükröt?

(4 pont)

Felvételi feladat (ELTE, 1964)

P. 3641. Egy neutroncsillag tömege kb. akkora, mint a Napé, sűrűsége mint az atommagé. Mekkora a neutroncsillag sugara? Mekkora a felszínén a nehézségi gyorsulás?

(4 pont)

Wigner Jenő fizikaverseny, Békéscsaba

A fizika feladatok megoldásai a következő címekre küldhetők:

KöMaL Szerkesztőség
Budapest 112, Pf. 32.  1518

megoldas@komal.hu (Az interneten keresztül történő beküldésről olvassa el tájékoztatónkat)

A beküldési határidő: 2003. október 11.